La curva de la p.

La curva de la p se centra en los valores significativos de p de los estudios primarios de un metanálisis y permite estimar, además del sesgo de publicación, si puede haber un efecto real tras el estudio, cuál es su magnitud y si existe sospecha de malas prácticas por parte de los investigadores para obtener valores estadísticamente significativos.
Seguro que todos conocéis la leyenda urbana de la chica de la curva, ese relato escalofriante de la misteriosa joven que aparece en las noches más oscuras en una peligrosa curva de la carretera. Un conductor desprevenido, un freno tardío y, ¡zas!, ahí está ella, con su vestido blanco y su expresión fantasmagórica.
Pero ¿y si os dijera que el mundo de la ciencia tiene su propia «chica de la curva»? No, no estoy hablando de un espectro vagando por laboratorios oscuros, sino de algo igual de intrigante: la curva de la p, la que forman los valores de significación de los estudios primarios de un metanálisis. Sí, esos números aparentemente inocuos, que indican la significación estadística, pueden esconder misterios y sorpresas.
Al igual que la chica que aparece en la curva, los valores de p pueden revelarnos si estamos ante un hallazgo auténtico o casual e, incluso, si algo más siniestro se esconde detrás de esos datos, que han podido ser torturados sin misericordia.
De hecho, observar la forma de la curva de los valores de p puede ser tan revelador como encontrarse cara a cara con la legendaria chica. ¿Estamos viendo un efecto verdadero, es un efecto espurio o, quizás, los datos han sido manipulados para forzar una conclusión estadísticamente significativa?
Si continuáis leyendo, veremos cómo nuestra chica puede ayudarnos a detectar los engaños y a buscar la verdad, tal como un conductor debe estar atento a las señales en la carretera para evitar un encuentro inesperado con lo desconocido. Así que abrochaos el cinturón y preparaos para un viaje fascinante por las sinuosas carreteras del metanálisis.
La incertidumbre del metanálisis
Afirman sus defensores a ultranza que el metanálisis es una herramienta poderosa y esencial en el mundo de la investigación científica. Al combinar los resultados de varios estudios, nos permite aumentar la potencia estadística, identificar patrones y subgrupos y mejorar la precisión de las estimaciones, lo que posibilita una mayor eficiencia en la toma de decisiones.
Todo esto sería así en un mundo ideal, en el que los metanálisis, sus estudios primarios y las personas que los realizan fuesen, a su vez, perfectos y honrados. Y esto, por desgracia, muchas veces está lejos de la realidad.
Hay, al menos, tres grandes enemigos del metanálisis como método de síntesis cuantitativa que pueden sesgar sus resultados. Vamos a verlos.
El sesgo de publicación
Lógicamente, para que las conclusiones de un metanálisis sean válidas, este debe incluir toda la evidencia disponible sobre el tema, lo que puede no ocurrir si no encontramos alguno de los trabajos (sesgo de recuperación) o si no se publican todos los trabajos que se realizan sobre el tema (sesgo de publicación).
Vimos en una entrada anterior que un estudio puede no publicarse por diversas razones, aunque lo primero que se nos viene a la cabeza es el problema de los estudios pequeños.
En principio, los estudios con tamaños muestrales más pequeños tienen más riesgo de no publicarse, salvo que detecten una magnitud de efecto grande. Estos suelen ser los que tienen un error estándar mayor y, por tanto, una estimación del efecto más imprecisa.
Pero, la verdad, es que hay un factor más importante que el tamaño del efecto sobre el riesgo de no ser publicado, y este no es otro que el valor de significación estadística del efecto medido en el estudio, el valor de p. En este mundo postrado a los pies de esta diosa arbitraria y de significado poco comprendido por muchos, es muy probable que un estudio que no tenga una p < 0,05 acabe archivado para siempre en el disco del ordenador del investigador.
Esto explica por qué los estudios con resultados negativos y no significativos tienden a desaparecer. En realidad, está relacionado, aunque indirectamente, con el tamaño muestral de los estudios: los más pequeños tendrán menos potencia, así que solo alcanzarán valores de p < 0,05 cuando la magnitud del efecto que detectan sea grande.
El azar, nuestro inseparable compañero
Al realizar un contraste de hipótesis establecemos una hipótesis nula y buscamos el nivel de significación estadística, el valor de p.
Si p < 0,05, rechazamos (por convenio) la hipótesis nula, lo que suele llevarnos a aceptar el efecto que observamos como real. El problema es que siempre corremos el riesgo de cometer un error de tipo 1 y detectar un falso positivo.
Esto ocurre también cuando observamos los valores de p de los estudios de un metanálisis: en promedio, en 1 de cada 20 estudios podemos encontrarnos, en realidad, ante un falso positivo.
Si torturas los datos lo suficiente, acabarán cantando
Ya hemos visto el culto a la p. Los estudios los realizan los llamados seres humanos, que siempre desean fama y prestigio, cuando no dinero, por lo que suelen verse presionados para obtener la ansiada p < 0,05. La consecuencia es que puedan emprenderse excursiones de pesca (lo que los amantes del inglés llaman p-hacking) con manipulación y sesgo de los datos, torturándolos sin piedad hasta que acaban por cantar una p estadísticamente significativa.
Para tratar de obviar todos estos inconvenientes, podemos recurrir a nuestra chica y su curva, la llamada curva de la p. Esta técnica se centra únicamente en los valores significativos de p de los estudios primarios del metanálisis y nos permite estimar, además del sesgo de publicación, si puede haber un efecto real tras nuestro estudio, cuál es su magnitud y si existe sospecha de malas prácticas por parte de los investigadores para obtener valores estadísticamente significativos.
Y todo ello sin necesidad de echar la culpa de todo a los estudios con menor tamaño muestral. Vamos con la curva de la p.
La curva de la p
La curva de la p, como dice su nombre, se basa en la forma de la curva de los valores de p de las estimaciones de efectos de los estudios primarios, pero solo de aquellos que son menores de 0,05. En realidad, más que una curva es un histograma de valores de p, cuya forma se supone que depende del tamaño muestral de los estudios y, lo que es más importante, de si existe un efecto real detrás de nuestros datos.
Para entender mejor cómo funciona, vamos a hacer una simulación con datos totalmente inventados que nunca nos encontraremos en nuestra práctica. Vamos a simular varios metanálisis con 5000 estudios primarios, en los que vamos a ir variando el tamaño muestral de los estudios primarios (n = 20, 50 y 80) y el efecto real que se quiere detectar (θ = 0, 0,3 y 0,5). Por último, asumimos que todos los estudios tratan de asumir un mismo efecto de la población o, lo que es lo mismo, un modelo de efecto fijo.
Una vez obtenidos los datos, elaboramos los histogramas con la frecuencia de los valor de p < 0,05.
En la primera figura vemos los histogramas para los tres tamaños muestrales cuando no existe efecto en la población (por ejemplo, una diferencia de medias estandarizada). En este caso, θ = 0.
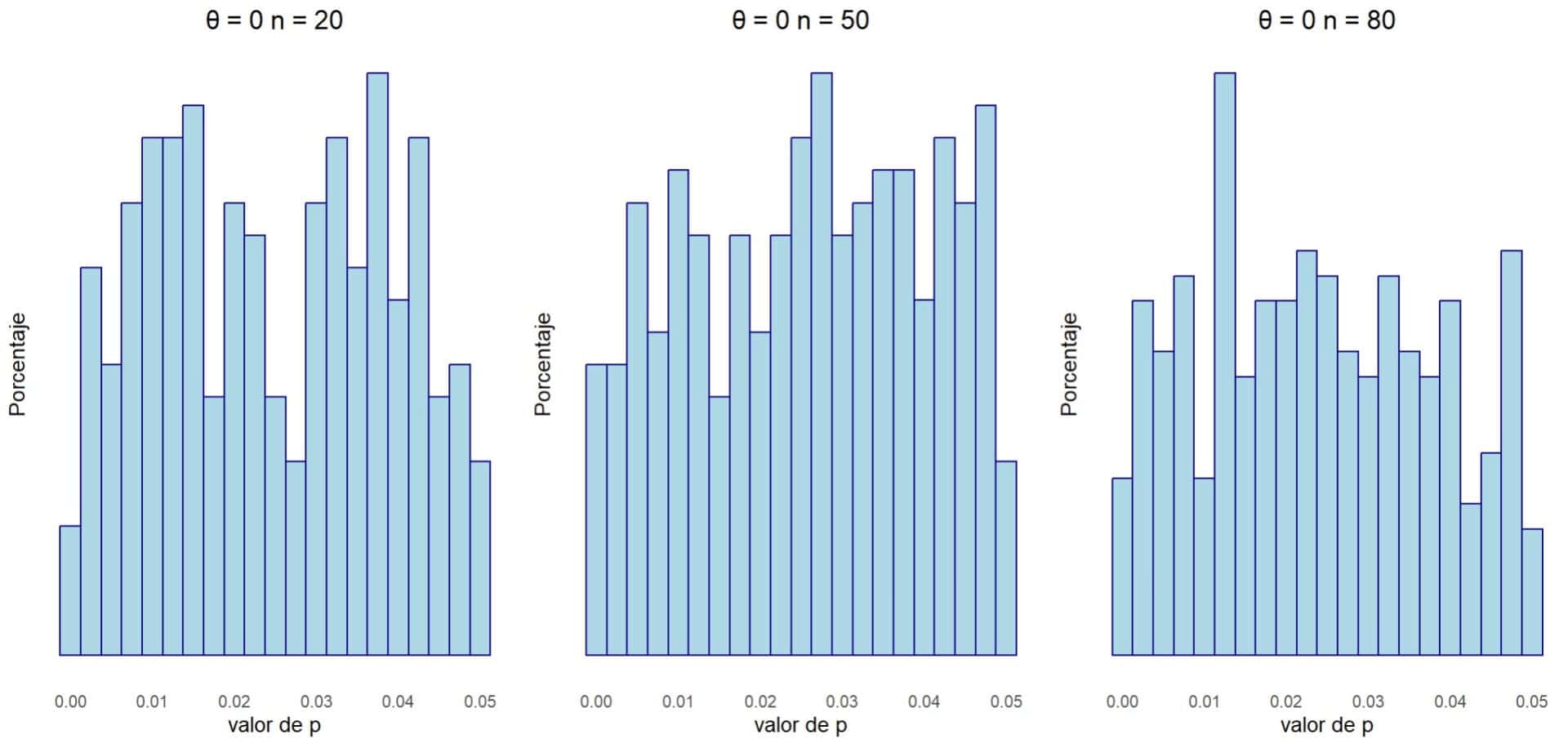
Vemos que, a pesar de que no existe un efecto real en la población (esta vez lo sabemos porque hemos generados los datos, pero es un dato desconocido que querremos estimar), obtenemos un valor de p < 0,05 en muchos estudios. No nos sorprende, es el error de tipo 1 entrando en acción: 1 de cada 20 contrastes, en promedio, será falsamente positivo, luego podemos esperar que 250 de los 5000 estudios detecten un efecto significativo solo por azar.
Eso sí, será igual de probable encontrar valores de p = 0,04 como de p = 0,01 o cualquier otro valor, por lo que los valores siguen una distribución uniforme. Además, esta distribución no varía al aumentar el tamaño muestral (y, por tanto, la potencia) de los estudios primarios. Si el efecto que queremos estimar en la población es 0, los valores de p se distribuirán uniformemente, con independencia del tamaño muestral de los estudios.
Cuando la curva de la p muestre este aspecto, podremos sospechar que no existe efecto poblacional y que los hallazgos observados son espurios, debidos al azar. Este es el tipo de curva cuando la hipótesis nula (θ = 0) es cierta.
Veamos ahora la segunda figura. Aquí hacemos las mismas variaciones con los tamaños muestrales, pero asumimos que sí existe un efecto real en la población, con θ = 0,3 y 0,5.
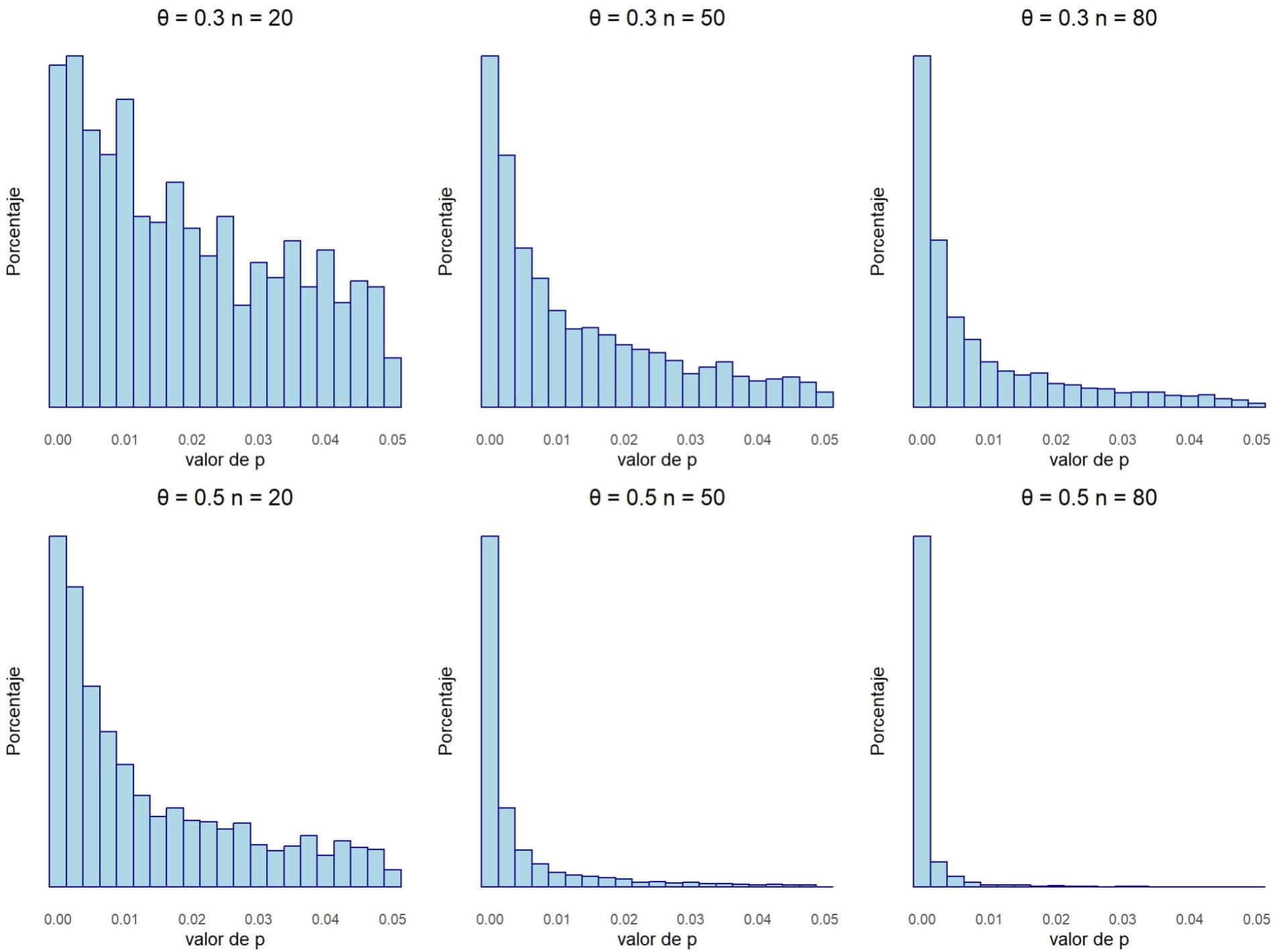
Cuando la hipótesis nula es falsa y existe efecto real tras nuestros datos, la forma de la curva de la p cambia de forma drástica. Ahora sí es más probable obtener valores de p más bajos (por ejemplo, p = 0,01) que aquellos que muestran significación marginal (por ejemplo, p = 0,045), con lo que los valores se acumulan a la izquierda y la curva tiene un sesgo hacia la derecha.
Este sesgo será mayor cuanto mayor sea el efecto real y cuanto mayor potencia para detectar el efecto tengan los estudios primarios (cuanto mayor sea su tamaño muestral). Podemos verlo comparando los seis histogramas.
En resumen, podemos sospechar que nuestros datos reflejan un efecto real cuando la curva de la p esté sesgada hacia la derecha. ¿Y qué pasa cuando los datos han sido torturados? Pensemos un poco y entenderemos cómo se modificaría la forma de la curva.
Habitualmente, los datos pueden ser manipulados para obtener significación estadística cuando el valor obtenido está próximo al de p = 0,05. Si está muy alejado, será difícil alcanzar la ansiada p < 0,05. Pero si está cerca, se pueden ir haciendo subgrupos, quitando datos con alguna excusa, moviendo otros de aquí para allá, etc, hasta que el valor de p caiga por debajo del umbral y se obtenga la ansiada significación.
En este caso, bastará con una p = 0,049, con lo que los esfuerzos por cambiar el resultado terminarán cuando se cruce el umbral de p = 0,05. Por esta razón, los valores de las p significativas se acumulan a la derecha del gráfico, con lo que veremos una curva de la p sesgada hacia la izquierda. Si vemos esto, olerá a chamusquina.
En teoría, cabe la posibilidad de que el torturador se esfuerce lo suficiente para bajar aún más el valor de p, pero es poco probable (aunque teóricamente posible) que consiga una curva con sesgo hacia la derecha. Hasta los medios más sofisticados de tortura tienen sus límites.
Y ahora que ya entendemos el concepto, vamos a ver cómo podemos cuantificarlo, recurriendo para ello a dos métodos: la prueba para el sesgo derecho y la prueba para una curva plana, también llamada prueba de potencia del 33%.
Prueba para el sesgo derecho
Podemos medir el sesgo derecho de la curva de dos formas. La primera, y más sencilla, es recurrir a la distribución de probabilidad binomial.
Si partimos el eje horizontal del histograma en dos mitades (en p = 0,025), podemos esperar que haya un mayor número de valores en la mitad izquierda cuando exista un efecto real y la curva esté sesgada hacia la derecha.
Vamos a suponer que tenemos un metanálisis con 30 estudios con p < 0,05, de los cuales 21 tienen p < 0,025. Asumiendo que, bajo la hipótesis nula de igualdad, hay igual número en ambas mitades (p = 0,5), podemos calcular la probabilidad de encontrar 21 o más con valores de p < 0,025. Si queréis podéis escribir el siguiente comando en R:
binom.test(21, 30, 0.5, alternative = "greater")$p.value
Nos da un resultado de p = 0,021, con lo que rechazamos la hipótesis nula y concluimos que existe un sesgo hacia la derecha.
La segunda forma de hacer esta prueba, un poco más compleja, consiste en calcular la probabilidad de obtener cada valor de p o inferior (una probabilidad acumulada que se denomina valor pp) y aplicar el método de Fisher.
Supongamos que tenemos 5 valores de p < 0,05: 0,01, 0,02, 0,02, 0,04 y 0,015. Bajo el supuesto de la hipótesis nula estos valores siguen una distribución uniforme, así que podemos calcular las probabilidades acumuladas (valores pp), multiplicando los valores por 20 (que es lo mismo que proyectarlos en el segmento [0, 1] en el que se distribuyen las probabilidades): 0,2, 0,4, 0,4, 0,8 y 0,3.
Ahora calculamos los logaritmos de los valores pp, los sumamos y los multiplicamos por -2, obteniendo el estadístico de la prueba, que sigue una distribución de la ji-cuadrado con 2k grados de libertad, siendo k el número de valores pp. Yo lo he calculado y su valor es de 9,74.
Si calculo la probabilidad de obtener un valor del estadístico como este o superior, es de 0,46, con lo que no puedo rechazar la hipótesis nula, que dice que los valores de p significativos siguen una distribución uniforme y que los hallazgos encontrados se deben probablemente al azar.
Prueba para curva plana
En el ejemplo anterior no pudimos rechazar la hipótesis nula. Esto puede deberse a dos razones. La primera, que no exista un efecto real detrás de nuestros datos. La segunda, que los estudios no tengan la potencia suficiente para generar un estadístico ji-cuadrado que alcance significación estadística. Cuando nos ocurra esto, podemos tratar de rechazar la hipótesis nula demostrando de forma empírica que nuestra curva de la p NO es plana.
En este caso, cambiamos el planteamiento de la hipótesis nula, que ahora afirmará que nuestra curva no es plana, sino que tiene un pequeño sesgo hacia la derecha, ya que los datos esconden un efecto de magnitud no muy grande (en caso contrario, lo habríamos detectado con el método anterior).
Este método se basa en calcular los valores pp asumiendo que el efecto es pequeño. ¿Cómo de pequeño? Por convenio, y de forma arbitraria, que pueda detectarse si la potencia de los estudios es del 33%.
El cálculo de estos valores pp es complejo e implica utilizar distribuciones de probabilidad no centrales, en las que no vamos a entrar ahora. Una vez calculado, procederemos igual que con el método anterior, pero con la diferencia de que tendremos poco interés en rechazar la hipótesis nula, ya que esto implicaría rechazar la idea de que existe un efecto real, aunque sea de pequeña magnitud.
Nos vamos…
No sé vosotros, pero yo estoy un poco mareado con tanta curva, así que vamos a ir tomando la recta de salida.
Hemos visto cómo algunos de los problemas del metanálisis se basan en suposiciones que muchas veces son solo eso, suposiciones, como la relación tan clara y tan directa entre sesgo de publicación y tamaño de los estudios que no llegan a publicarse.
Además, hemos conocido una herramienta nueva que nos permite tratar de sospechar si podemos estar ante efectos reales o antes hallazgos espurios, simples falsos positivos debidos al azar y a la metodología con la que se realizan los contrastes de hipótesis.
Por si fuera poco, estos métodos nos pueden hacer sospechar que haya podido haber manipulación de los datos para conseguir la significación estadística, con lo que la confiabilidad de los resultados del metanálisis perderá su valor.
Como siempre os digo, lo importante es entender el concepto y no tratar de hacer estas pruebas a mano. Todos los métodos que hemos visto pueden hacerse con paquetes estadísticos o con calculadoras existentes en Internet.
Os decía al principio que la curva de la p puede servirnos también, no solo para sospechar la existencia de un efecto real, sino para estimar su magnitud. Eso implica métodos algo más complejos y el empleo de las distribuciones probabilidad no centrales que hemos mencionado de pasada y que representan la distribución de los datos cuando la hipótesis cierta es la alternativa y no la hipótesis nula. Pero esa es otra historia…

Muy buena explicación
Mi temor en la data, la influencia como diría Quevedo » poderoso caballero don dinero»
Gracias Ricardo por el comentario.
Esa es una de las causas que nos obligan a aprender lectura crítica.
Saludos
Manolo
Mi temor siempre fue que el análisis de los distintos trabajos tengan un sesgo económico. Recordando las palabras de Quevedo » Poderoso Caballero Don Dinero «.