Egger’s test.

In the 17th century, an alchemist named Hennig Brand was convinced he could turn urine into gold. He spent years collecting large quantities of this liquid and performing countless experiments in his laboratory. After much effort, he came up with the idea of ​​boiling the urine to remove the water and, once again, heat the solid residue obtained and collect the steam that came out.

When this vapor cooled, a white, cerulean-looking material remained, which turned out to be phosphorus, an element unknown until then.

Thus, although he did not manage to get the gold he was looking for, he was rewarded by another no less important discovery. The alchemist was lucky and, although his initial goal was based on an erroneous assumption, the process led to a significant discovery. This curious history of alchemy has an interesting parallel with certain modern tools of the science of meta-analysis.

Take, for example, Egger’s test. This test is used in meta-analyses to detect publication bias, based on the unproven idea that smaller studies are more easily published when they show larger effects, which can be significant, despite their lower precision.

Known as the small studies effect, this assumption is not without controversy. Some authors believe that this tool is essential for unmasking hidden biases, while others argue that relying on it is like following an alchemical recipe without a clearly demonstrated foundation and that it may not always deliver the gold it promises.

If you continue reading this post, we will explore the mysteries and realities of this test and discover if it can really turn the lead of data into the gold of truth of statistical inference.

It all starts with a funnel

We already saw in a previous post how the funnel plot is the most used graphic tool to assess the possible existence of a publication bias in a meta-analysis.

It is based on the small study effect that we have already discussed a little above. According to this effect, the statistical significance value of the result of a study, its p-value, is one of the most important factors that can influence whether the study is published or remains in a researcher’s drawer.

According to this, small studies are only accepted for publication if their result is significant. As these small studies tend to be less precise (due to their smaller sample size) and their confidence intervals are usually wider, they will only reach statistical significance if the effect they detect is large. In the case of small effects, it will be more likely that the confidence interval crosses the null value, and the p does not reach the desired value below 0.05.

The funnel plot represents the effect measure (x-axis) against a precision measure (y-axis), which is usually the inverse of the sample size or the inverse of the variance or of the standard error. If we represent each primary study in the review, the most precise studies will be in the upper area, which are usually those with the largest sample size. Being more precise, they are grouped around the summary measure with little dispersion. You can see it in the attached figure.

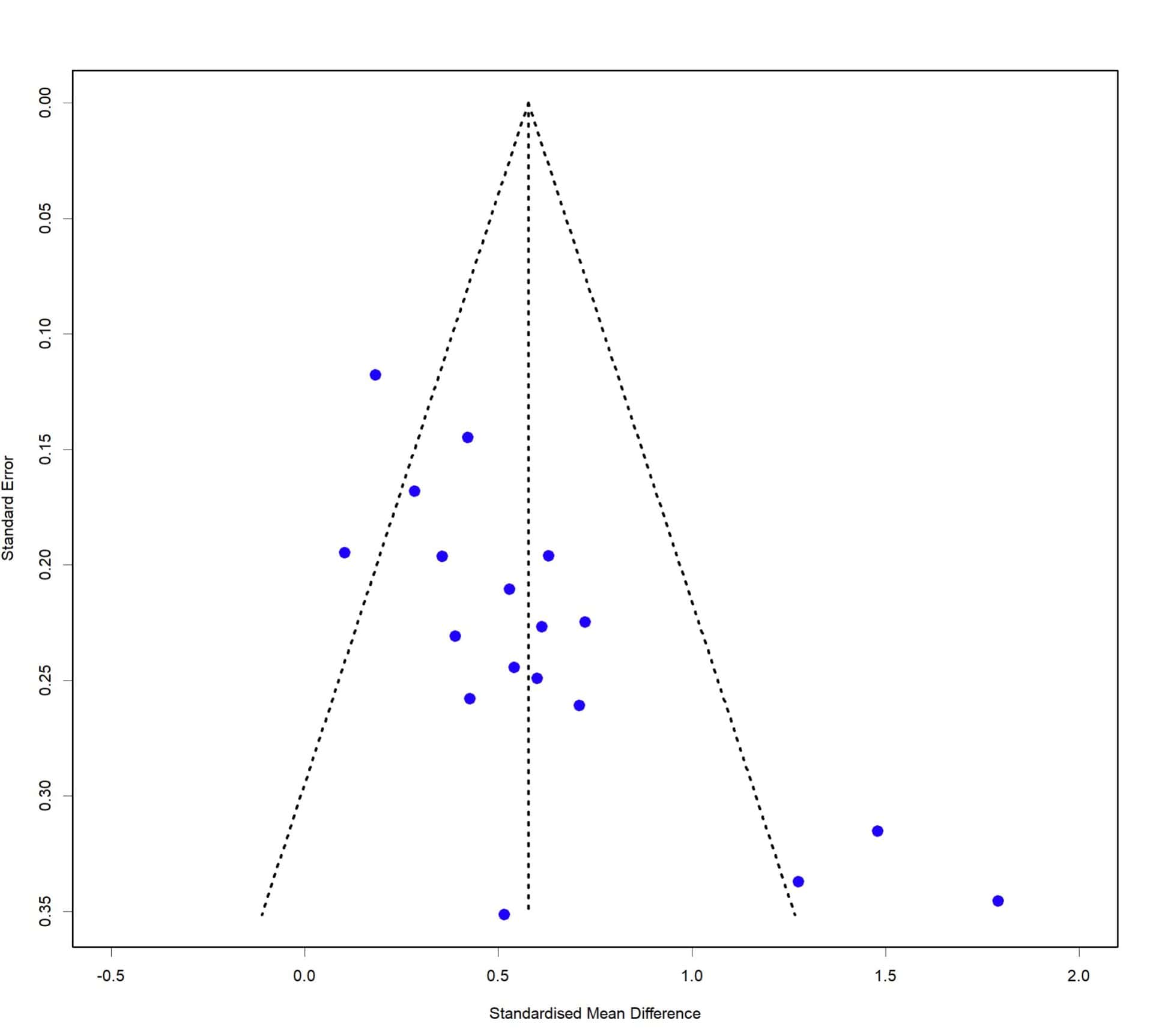
As we move towards the origin of the y-axis, the studies are less precise, so they are dispersed more widely around the value of the summary measure of the meta-analysis.

If the effect of small studies is true, imprecise studies with large effects will be overrepresented, generally those with results favourable to the intervention under study. Those that are not significant or unfavourable will have a greater risk of not being published, which will produce an asymmetry in the distribution of the points that represent the studies in the meta-analysis.

This asymmetry will make us suspect the existence of publication bias, although we already know that it may also be due to other reasons, such as heterogeneity between primary studies.

Thus, the funnel plot is a simple and easily interpreted tool for assessing this bias so characteristic of meta-analyses. However, the problem that arises is that it is a subjective method that depends on the criteria of the person evaluating the graph. In some situations, especially when the number of studies is small, it can be difficult to estimate whether or not there is asymmetry in the funnel. We therefore need methods to objectively quantify this asymmetry.

It is in these cases when we can perform the Egger’s test.

Egger’s test

Egger’s test is the most popular quantitative method to assess funnel plot asymmetry. It is based on a linear regression model between the measure of effect and the precision of the studies, as shown in the following equation:

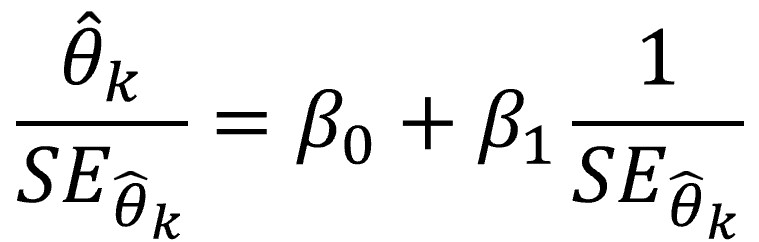
Let’s think a little about what the previous formula tells us to better understand how this test works.

The dependent or response variable is the estimate of the value of the study effect divided by its standard error. In reality, what we do is standardize the measure of the effect, with which we obtain a z score.

Using a z score is very useful, since we can know if the estimated effect is statistically significant just by looking at the value of the score. As we already know, for a normal distribution and a significance threshold of p < 0.05, the effect will be significant if the z score is greater than +1.96 or less than -1.96 (for a two-sided contrast).

The Egger’s test model regress this z score on the inverse of the standard error of the studies, which is equivalent to their precision (the lower the precision, the higher the standard error).

But what interests us in this case is not the coefficient β₁ of the slope of the line, but the value of β₀, which must be significantly different from zero when there is asymmetry in the funnel. Why? Let’s see it.

As in any linear regression model, β₀ represents the value of the response variable when all predictors are zero. Since the predictor represents the precision of the study, the intercept represents the value of z when the precision is zero (when the standard error is infinitely large).

In the absence of publication bias, the effect sizes of individual studies should not be correlated with their precision (represented by the inverse of the standard error). In this case, the effects of individual studies should be distributed symmetrically around the true summary effect (regardless of its precision), without any systematic deviation from this distribution.

In terms of regression, when plotting the effect size against its precision, the line of best fit should pass through the coordinate origin. That is, the intercept of this regression should be zero, indicating that there is no systematic deviation of the effects of the studies based on their precision.

However, when there is publication bias, the fact that less precise studies with small effect sizes are not published causes a systematic bias that favours imprecise studies with larger effect sizes. This produces a bias in the effect size with respect to its precision, so that the regression line no longer starts from the origin of the coordinates and the intercept is different from zero.

In summary, a non-zero intercept suggests that less precise studies (with higher standard error) tend to estimate systematically different effect sizes than more precise studies, which is an indication of publication bias, where studies with non-significant results or negative ones are not published with the same frequency as those with positive and significant results.

A practical example

Let’s see how this test is carried out with a practical example. I am going to use the R program and the same set of data with which I drew the funnel plot that we saw at the beginning of this post.

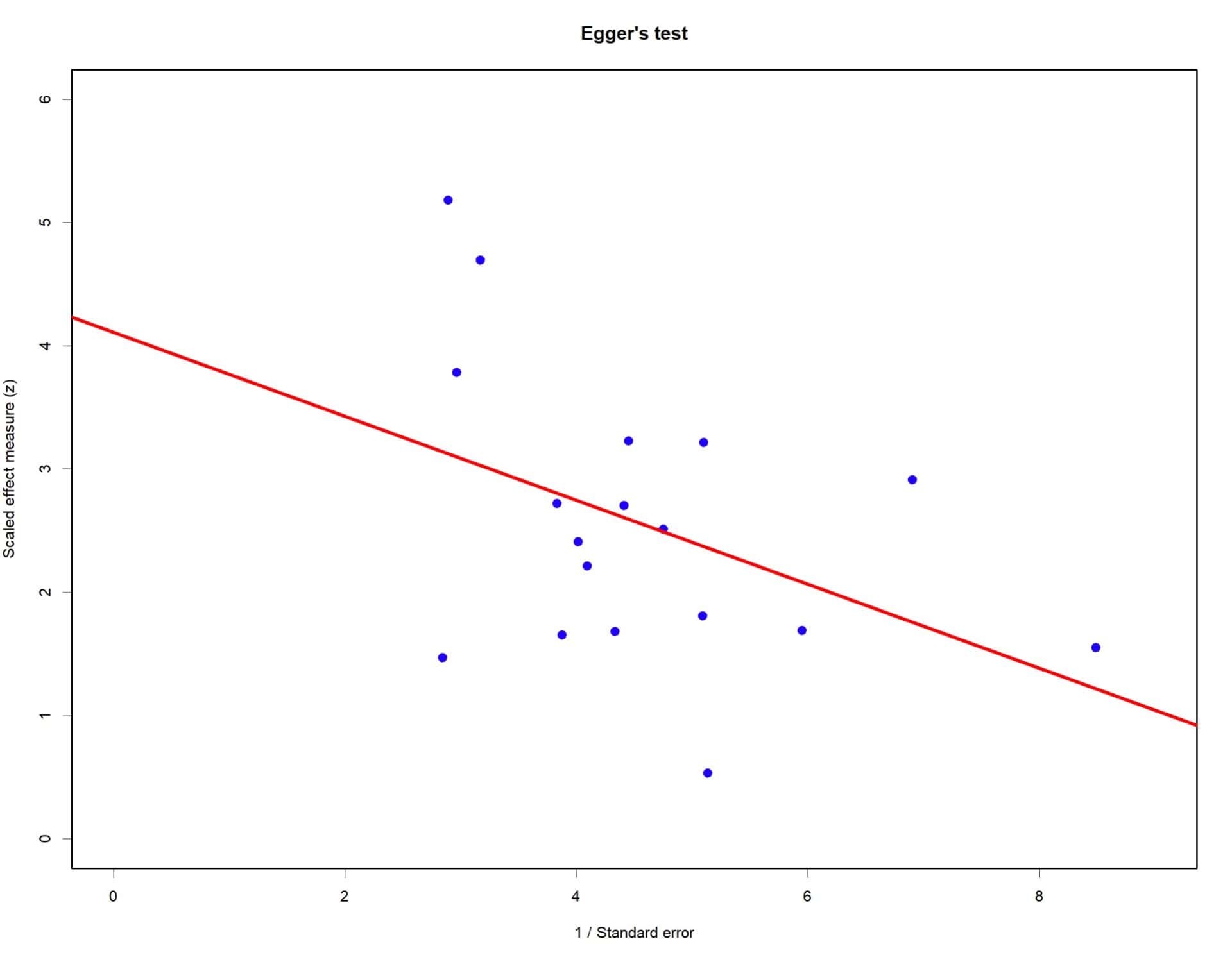
I am not going to bore you with the R commands, which are not very complicated, and I will only tell you that, after calculating the regression model, it gives me an intercept value of 4.11.

R performs a hypothesis contrast assuming the null hypothesis that the intercept is equal to 0. It obtains a value of t = 4.68 with 16 degrees of freedom, which calculates a value of p = 0.0003. Therefore, with p < 0.05, we reject the null hypothesis and assume that the intercept is different from zero, indicating an asymmetry in the funnel plot (probably due to publication bias).

We can represent the regression model and the primary studies, as they appear in the next figure. As we already know from the numerical contrast, the origin of the line does not pass through the origin of coordinates.

Peters’ test

We saw in the previous example how the relationship between effect size and standard error is established in the case of a meta-analysis whose effect measure is a standardized mean difference.

This dependence also occurs in meta-analyses with results with binary variables (relative risks, odds ratios, etc.). The problem in these cases is that these measurements do not follow a normal distribution, so performing the Egger’s test has the risk of producing an increase in false positives.

In these cases, we can resort to a variation known as the Peters’ test which, also under a random effects model, establishes the regression model between the log-transformed effect (so that it fits a normal distribution) and the inverse of the sample size. For formula lovers, I show it below:

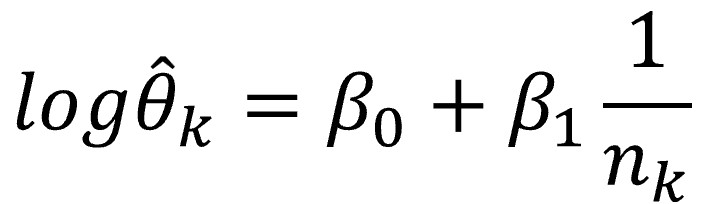
The Peters’ test regression model is a little more complex than that of the Egger’s test, since it performs a weighted regression. This means that each study is weighted based on the sample size and the number of events observed and that the model is calculated with a modification of the least squares method that takes these weights into account.

This weighting ensures that studies with larger sample sizes and more events have more influence in determining the relationship between effect size and precision. I am not going to show you more formulas, since as is usual, no one performs these calculations by hand, but rather using computer packages.

As with Egger’s test, Peters’ test is based on the relationship between the precision of the studies and their effect estimates. In the absence of publication bias, there is not expected to be a systematic relationship between effect size and study precision (which is inversely related to the standard error).

However, in the presence of publication bias, studies with lower precision (i.e., with higher standard error and generally with smaller sample sizes) tend to estimate larger effect sizes due to the preference for significant and positive results (which are overrepresented because they are more likely to be published).

Unlike Egger’s test, in Peters’ test we are not interested in the intercept, but rather in the slope of the regression line, the coefficient β₁: a significant slope (different from zero) suggests a relationship between precision and effect size and, therefore, the presence of publication bias.

In particular, a negative slope will indicate that less precise studies (with larger standard errors) tend to estimate larger effect sizes, which is, again, an indication of publication bias.

The procedure with a statistical package is similar to what we have seen with the Egger’s test, with the difference that this time the hypothesis test will be done for the slope of the regression line and not for the intercept.

Return to alchemy

We already saw at the beginning of this post how our poor Hennig Brand failed to obtain the gold because his methods were based on theories that were not very well proven, to say the least.

Well, something similar happens with the Egger’s test, as we have already commented with the assumption of the effect due to small studies. This leads to some opinions that question the robustness of the Egger’s test for assessing publication bias.

Firstly, it is very sensitive to sample size. Studies with small sample sizes can generate misleading results, as the statistical power of the test decreases with small samples, which could lead to a high rate of false negatives (not detecting an existing publication bias). In general, both the Egger’s and Peters’ tests may be of little power when the number of studies is small, and their use is not recommended if there are less than 5 primary studies in the meta-analysis.

As if that were not enough, a small number of studies or with very different sample sizes can put at risk a necessary assumption to apply the test: that the standard errors of the studies are normally distributed.

Furthermore, we have already commented that Egger’s test can give erroneous results when there is high heterogeneity between studies, confusing this with publication bias. This can increase the number of false positives when there are methodological differences between studies (of course, in this case, the appropriateness of conducting the meta-analysis may even be questionable).

We’re leaving…

And here we are going to leave alchemy for today.

We have seen how to quantify funnel plot asymmetry in a more objective way to try to detect the possible existence of publication bias in a meta-analysis. Egger’s test is a simple technique to perform and interpret, although it has, as we have seen, some drawbacks, so it should be used with caution and, if possible, in combination with other techniques designed for the same purpose.

That is why some more robust alternatives have been proposed, such as the Peters’ test that we have described in this post, although there are some more, both graphical and analytical.

One of them is the so-called modified Egger’s test, which attempts to improve robustness against heterogeneity and reduce the number of false positives of the test. This can be done by applying sample size weights or transformations of the results, such as logarithmic transformation. But that is another story…