Overfitting.

Did you know that there’s a theory that suggests that if you sync Pink Floyd’s The Dark Side of the Moon album with the movie The Wizard of Oz, you get a surprisingly coherent audiovisual experience? This idea, known as “The Dark Side of the Rainbow,” has fascinated fans and the curious for years. It’s said that from the moment Dorothy begins her journey to the land of Oz, Pink Floyd’s music seems to eerily coincide with the action of the film. Coincidence? Or something deeper?

This is where apophenia comes into play, that psychological phenomenon in which we so-called human beings find meaningful patterns in random data. The most common form of apophenia is pareidolia, which happens when we see images of faces or animals where there are none. Who hasn’t seen a cute little pig where there’s nothing but an innocent cloud?

The fascination with “The Dark Side of the Rainbow” is a perfect example of how our minds seek and find connections even where there aren’t any. As Dorothy follows the yellow brick road, our brains tend to create narratives, seeking to make sense of everything from song lyrics to rhythm changes in music.

And what does this have to do with statistics? More than one might think, actually. Apophenia is a common trap that algorithms trying to interpret our data can fall prey to, so it’s crucial that we’re aware of it. Of course, in this world of data and patterns, we’ve invented another word that, much less sonorous, has become more famous than apophenia: overfitting.

In today’s post, we’ll explore how this natural tendency can influence research and data analysis, leading us to see patterns that don’t exist and jump to conclusions. So, just like with “The Dark Side of the Rainbow,” we need to be alert and critical so as not to get carried away by the magic of coincidences.

Learn from the data, but don’t memorize it

How much simpler it would be if we could give this advice directly to our algorithms when they start training data! Being able to do this would help make the difference between getting models that make useful predictions or, on the contrary, developing totally useless ones.

To clarify things a bit, let’s remember that an algorithm is a set of sequential instructions designed to solve a specific problem or perform a task. Let’s take, as an example, a very simple one: simple linear regression.

A simple linear regression model tries to predict the value of a dependent variable (y) based on the known value of an independent variable (x), according to the following equation, which is known to everyone:

y = a + bx

In a model like this we have two parameters, a and b (the intercept and the slope of the line), which will allow us to estimate the value of y for a given value of x. Our function will be to find the values ​​of the parameters that allow us to make a better estimate.

In this case we could choose to solve for the coefficients using the least squares method, since we have a known algebraic solution. But there is another way to do it, which is to build an algorithm and train it with a sample of data to find these optimal values ​​for the coefficients.

In a typical supervised machine learning approach, you input the values ​​of 𝑥 and tell the algorithm what values ​​of 𝑦 to predict, so it adjusts the coefficients to minimize the prediction error.

During training, the algorithm learns from the data the best parameters for the model. It starts with random values, compares the prediction to the expected value, measures the error, and iteratively adjusts the parameters to reduce the error to the minimum possible. In short, the algorithm learns the relationship between the data and finds the optimal values ​​for the model parameters.

The problem of overfitting

Overfitting occurs when an algorithm learns the details of the training data too well, capturing not only the essence of the relationship between them (if there is a relationship, of course), but also the random noise that will always be present.

This negatively affects its performance when we introduce new data, not seen during training. Following the analogy between “learning” and “memorizing,” the algorithm “memorizes” the training data instead of “learning” from it. This means that the model will work exceptionally well on the data set it has seen before but will fail to generalize when presented with new data.

Consider for a moment the importance of the problem. We have a sample of data, but our interest is not in making predictions on that sample (in fact, we know the value of “y” that it must predict), but on new data in which the value of “y” is unknown.

We can always make the algorithm learn the data by heart, even if we give it a random data set, without any existing relationships or patterns, but this will be useless for making new predictions.

The solution is in the data

Let’s see how we have to organize our data during the training phase to avoid overfitting of the model.

The first thing will be to obtain a data set representative of the problem we want to solve. Then we will have to clean and transform the data into the most appropriate format for the algorithm we want to train (missing or anomalous values, normalization, coding of qualitative variables, etc.).

Once the data is prepared, we divide it into three sets: training, validation and test. A larger proportion is usually left for training, between 60-80%, depending on each case, and the rest for validation and testing.

We are now ready. We begin training with the data set for, oh surprise!, training.

Training

The algorithm starts to iterate, adjusting its parameters in each turn to progressively reduce the error of the predictions. When do we stop this process and stop going around? It will depend on the data and the nature of the algorithm, but we can reason how to choose the optimal moment for each case.

If we stop too early, the algorithm will not have adjusted its parameters as much as possible, so the resulting model will make predictions that are less precise than those we could have achieved. During this first phase of training, underfitting occurs, in which we have not yet achieved the best possible performance.

On the other hand, if we stop too late and the algorithm performs more iterations than necessary, there will come a time when it stops learning from the data and start learning it by heart. We have entered the realm of overfitting: the algorithm’s error with the training data will tend to zero, but its prediction capacity will also decrease with new data.

It seems obvious that we need to stop at the right time, neither too early and suffering from underfitting, nor too late and suffering from overfitting. How do we do it? By using the data set we reserve for validation.

Validation

The solution is to perform training simultaneously with the training and validation sets. The trick is to use only the training data to adjust the algorithm parameters. The clue as to when to stop training is given by the graphical representation of the accuracy of the predictions and the magnitude of the error as a function of the iterations of the algorithm, as shown in the following figure.

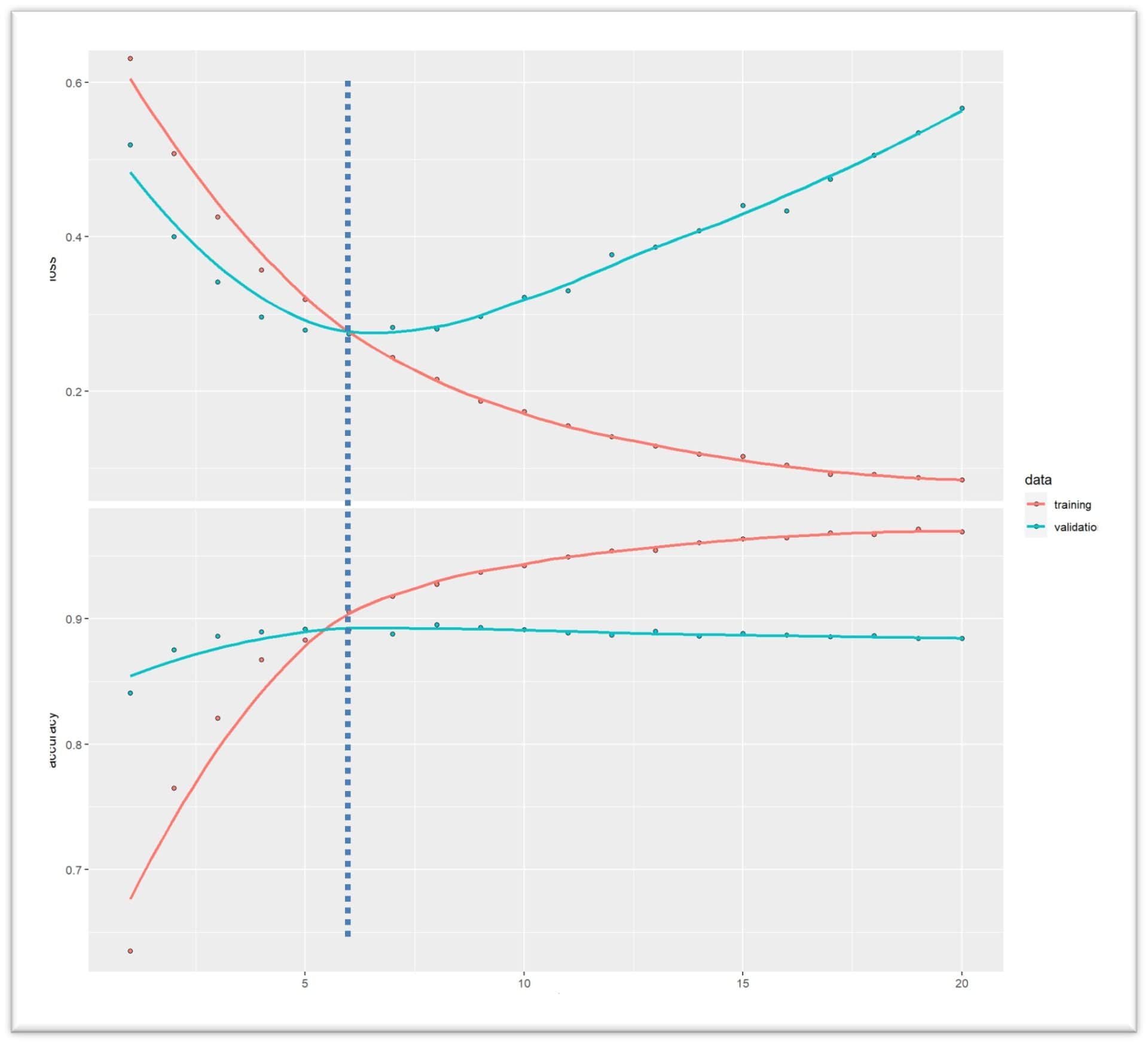
The graph represents the iterations of the algorithm (x-axis) versus the error of the prediction in each iteration (top) and the accuracy of the predictions (bottom), both for the training data (red line) and for the validation data (blue line).

Let’s look first at the training data. As we have explained, as the number of iterations progresses, the error decreases more and more until it tends to a minimum value close to zero, while the accuracy increases, more or less quickly at the beginning and stabilizing at a maximum value after a certain number of iterations.

So far, there are no surprises, but if we look closely, the same does not happen with the validation data. The key is to remember that the adjustment of the parameters is done with the training set. At first, the algorithm learns the data and captures the relationship between them. Since the validation data is from the same sample as the training data, the same phenomenon occurs with the error and the accuracy of the predictions.

But there comes a time when the algorithm stops learning and starts memorizing: we enter the overfitting phase. From here on, what it does is capture the noise of the training data, so the results with the validation data are no longer as good: the accuracy stagnates at a value lower than the accuracy of the training data and the error rate stops decreasing or even increases, worsening the performance of the algorithm with the validation data.

As you can see in the graph, marked with the vertical dotted line, this occurs after 5 iterations of the algorithm. Until then, we were in underfitting. From then on, we enter overfitting. I would say that the best model for this case can be achieved with 5-6 iterations of the algorithm. Not only are more iterations not necessary, but we would worsen its performance with new data.

Test

We have one set of data left that we have not used yet: the test set. Those of you who are more awake will already imagine why we have kept it. Indeed, to test the model once it has been trained.

You may wonder why we need to perform another check of the model’s performance, if we have already done so with the validation data. The reason is because the model has been trained by adjusting its parameters taking into account its results with the validation data as well. This causes part of the information from the validation data to “leak” into the training’s, so the correct thing to do, once trained, is to measure its performance with a set of data not used until now: the test data.

As a general rule, performance will be higher with the training data, followed by the validation data and, thirdly, the test data.

And that’s not all. In order to better generalize the model’s capacity for the task for which it has been developed, an external validation will have to be done with new data that comes from a different population from the one from which we obtained the training, validation and test data sets.

Overfitting: friend or foe?

At this point we may think that overfitting is an enemy to beat in our fight to obtain the best predictions with our data, but let’s think for a moment if we are interested in getting rid of it.

When we start training, we are in the underfitting phase. If we stop here, the model will be improvable and will work at a suboptimal level. When do we know what the optimal point is to train up to? Obviously, when overfitting begins, or a little before.

Clearly, not only are we not interested in doing without it, but the ability of a model to overfit the data is essential to achieve the optimal model.

Once again, the virtue lies in the middle. We want the model to be able to overfit, but not too much. There are various reasons that can lead a model to overfit excessively.

One of them is the complexity of the model. The more complex it is, the more likely there is a risk of overfitting. Deep neural networks with many layers or decision trees with great depth have the ability to capture even the smallest variations in the training data. This can lead to the model not only learning the true relationships in the data, but also noise and irregularities.

Another common problem is having insufficient data for model training. If the training data set is small, the model will not have enough information to learn general patterns. Instead, it will learn the specific details of the limited data set, leading to overfitting.

For many of these problems, there are techniques that help us mitigate the risk of excessive overfitting.

The first thing would be to use a less complex model or, failing that, try to simplify the model we intend to train.

When the data is insufficient, we can resort to data augmentation techniques, as is often done in some computer vision models that use convolutional neural networks. In any case, the quality of the data must always be taken care of, processing it appropriately, recoding variables, etc.

When there is too little data to split into the three subsets we mentioned above, we can use cross-validation techniques. These split the dataset into multiple subsets and train the model multiple times, each time using a different subset as the validation set. This helps ensure that the model generalizes well to different parts of the data.

Finally, we have already seen how early stopping training is one of the most powerful weapons we have to prevent excessive overfitting of the data, ruining the generalization capacity of the model obtained.

We are leaving…

And here we will leave the fitting for today.

We have seen how overfitting is a common and critical challenge in the training of algorithms that, although it was already present in the most classic statistical models, takes on special importance with the more complex machine learning and deep learning models that are currently being developed.

Understanding how it occurs and applying the appropriate techniques to prevent it is essential to build models that not only work well with known data, but are also able to generalize to new data. Let us always remember: learning from data is essential, but memorizing every detail can be counterproductive. In statistics and data science, as in life, balance is the key.

We have briefly seen some strategies to keep overfitting at bay, but we have not said anything about some techniques that are used with more complex models, such as regularization techniques, which penalize the complexity of the model, discourage excessive overfitting of training data, and favour the generalization of results with new data. But that is another story…