Ensemble decision trees.

In the heart of the frozen, distant Winterfell stood the majestic weirwoods, white trees with red leaves and faces carved into their bark. These sacred trees were imbued with supernatural magic and revered as bearers of ancestral memory. It is said that through them, the children of the forest and the white walkers could spy on the living.

So these mystical trees not only held ancient secrets, but, like our decision trees, they had the ability to “predict” and “decide” the course of crucial events in the fabric of time. The Starks sought advice from these trees before making big decisions, much like how we, today, consult our own decision trees in the world of data science.

Who wouldn’t want a tree in their backyard to whisper secrets and guide them through uncertain times? Luckily, although weirwoods no longer exist in our world, we do have our mystical decision trees. While they are not made of wood or have red leaves, the trees we will look at in this post, from the solitary decision tree to the complex and dense random forests and other ensemble decision tree techniques, can help us navigate the intricate forest of data to make predictions and guide our decisions.

Each type of tree in the world of data analysis has its own charm and purpose, just as each weirwood had its sacred place in the forests of Winterfell. So, if you have ever wondered how they can help us “predict” the future, read on and we will discover the secrets they hold.

The problem statement: ensemble decision trees

We saw in a previous post how decision trees recursively divided the space of predictor variables in order to estimate or predict the value of the target response variable, which can be either numerical (regression trees) or nominal (classification trees).

In addition, they allowed, in a relatively simple way, to visualize and interpret the data. The problem with simple decision trees is that they do not usually achieve precision values ​​as high as other regression or classification algorithms, in addition to being not very robust in the sense that small variations in the data or in the selection of the variables can lead to large changes in the trees that are built and in their performance.

Putting a little imagination into the matter, we can see these simple trees, with little predictive capacity, as a series of blocks that we can combine in various ways to obtain a much more powerful and precise model. These are the ensemble decision tree models, which demonstrate another case of application of that old aphorism that unity is strength.

In this post we are going to talk about three types of ensemble decision trees: those built using resampling aggregation techniques, the so-called random forests, and those that learn from their predecessors to boost their performance.

Don’t worry, it’s not as exotic as it seems from the previous paragraph. As we will see, it’s about combining other statistical and data science techniques to produce many trees that work better than the original.

Resampling and aggregation (bagging)

Bagging is not a word as such, but rather the abbreviation of bootstrap aggregation.

We already talked about bootstrapping or resampling techniques in a previous post, so you can read it if you want to refresh the subject. The bagging method builds ensemble decision trees by aggregating trees and using bootstrap techniques, as its name indicates. Let’s see how.

The balance between bias and variance

When we are developing any regression or classification algorithm, we always wonder what these two characteristics of the algorithm are like: bias and variance.

Simply put, bias is the tendency of the model to make systematic errors due to simplified assumptions about the nature of the problem. A model with high bias does not have the ability to capture the complexity of the data. For example, a simple linear model will not be able to adequately capture the relationship of a set of data that follows a quadratic trend. This model will have high bias, the model will fit below the optimal level, and its predictions will have a high error.

Variance, on the other hand, refers to the sensitivity of the model to small fluctuations in the data set with which it is built, the training data. A model with high variance causes it to not only capture the relevant patterns in the data, but also adapt too well to the particular data used and learn the noise or specific peculiarities of that data. This will result in overfitting: the model will work very well with the training data, but will not be able to make correct predictions when we confront it with new data.

Bias and variance are inversely related in what is known as the bias-variance trade-off. A model with low bias tends to be very flexible and able to capture complexities in the data, but this also makes it susceptible to high variance. Therefore, it is essential to find an appropriate balance between bias and variance to achieve a model that generalizes well and performs well on both training data and new data.

This problem occurs with simple decision trees, which, as we have already mentioned, are very weak against small variations in the data. In other words, they have a high variance and a tendency to overfit.

Bagging is one of the techniques that allows us to control this balance and reduce the variance during the training of the algorithm. Behind this methodology lies a fairly simple idea.

Imagine that, from a given population, we have extracted 10 samples, and we have measured a certain quantitative variable. Each of these samples will have its mean, with more or less similar values, and, let’s assume, the same variance, the population variance.

Now we can use this sampling distribution and take the results of the 10 samples and average them. The overall mean will be the average of the 10 individual means, but the overall variance will be equal to the population variance divided by the sample size (10 samples, in this case).

That is, if we have a set of observations from the same population, we can average them to obtain their mean and their variance, so that the latter will be lower than that of each set separately.

This is the principle behind bagging, averaging many trees to obtain an accurate prediction and reduce the variance. The problem here is obvious: we usually do not have multiple sets of data from the population. Well, this small inconvenience can be solved by creating multiple samples from the available sample using bootstrap or resampling techniques.

Each bootstrap sample is obtained by randomly selecting, with replacement, examples from the original data set, so that each sample may contain duplicates and may omit some original examples. Once the samples are obtained, a simple independent decision tree is trained with each of them.

In this way, we will have created a N number of decision trees, each one with little bias and a lot of variance. By averaging the predictions of these N trees, we can get a prediction with a much lower variance, that is, with less overfitting, improving the capacity of the model to generalize its predictions to new data.

And this not only works for regression trees, but also for classification trees. In these cases, we take the predictions from the hundreds or thousands of trees that we create and make a kind of contest, awarding the category predicted most frequently among the total set of predictions.

A practical example

We already saw how to make a simple decision tree in a previous post, using the R program and the “mtcars” dataset, widely used for this type of examples, which contains information about different car models and their characteristics. It includes 32 rows (one for each model) and 11 columns that represent various car characteristics, such as fuel efficiency (mpg), number of cylinders (cyl), displacement (disp), engine power (hp), rear axle ratio (drat), weight (wt), etc.

In this case, we are going to predict fuel efficiency (miles per gallon, mpg) based on the rest of the variables. Those who like to get to the bottom of the matter can download the complete R script at this link.

Using the randomForest library in R, the command to generate the model allows for a number of parameters, such as the dependent and independent variables, the data set used, and two parameters to decide how many trees we generate and how many variables are considered at each decision node in the tree. In the case of bagging, all variables are considered, but this changes with other types of ensemble decision trees, as we will see later.

In our case, we asked R to make 100 trees and, of course, to use all the predictor variables.

R builds the model and tells us that it includes 100 trees, that it has taken into account 10 variables at each node, that the mean square of the residuals is 6.55, and that the model explains 81.4% of the variance of the dependent variable. Not bad at all! Consider that this would be the equivalent of a regression model with an R² of 0.81.

Now, I’m sure you’d all like to draw the tree, but think about it for a moment… how can we draw it if it’s the combination of 100 different trees? The answer is that we can’t. We’ve just lost one of the advantages of trees, their easy graphical interpretation, in exchange for improving their predictions when we confront them with new data. You see, in statistics and data science it’s common that, in order to improve a feature, we always have to give up something.

But don’t despair, we have a resource that can be similar or even better than the graphical representation: the importance of each variable.

Some are more important than others

Like the animals on Orwell’s farm, all variables are equal, but some are more important than others. Not all of them have the same influence or utility in helping the model make accurate predictions.

When I talked about the parameters of the randomForest() function above, I left one out, the importance parameter. If we give this parameter the value True, the model calculates and saves measures that indicate how important the different variables are in predicting the target variable.

To do this, the algorithm alternates between the different variables, testing which of them reduces the error function the most when used in a certain node of the tree division. The mean square error is usually used for regression trees and the average reduction in Gini impurity for classification trees, as we saw in the post about simple decision trees.

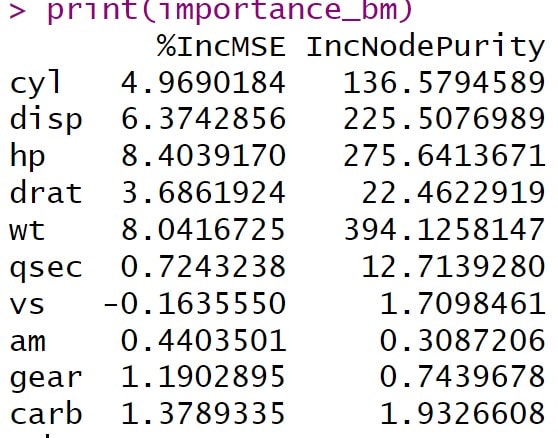
The R program gives us a table with the predictor variables and two columns, the percentage of increment in the mean square error and the node purity increment (we will now see why it gives us this second column, even though it is a regression tree). You can see the result in the attached table.

Let’s start with the percentage increase in the mean square error. The variable hp, the vehicle power, has the highest value, 8.4%, suggesting that it is the most important variable for predicting the dependent variable mpg. When the variables are randomly permuted, the permutation of hp increases the model error by 8.4%, suggesting that it is an important variable.

Next, we see that wt (8.04%) and disp (6.37%) also have a high impact on predicting mpg, being the most important variables after hp. On the other hand, the variable vs has a negative value, indicating that its exclusion slightly improves the performance of the model, and the variables qsec and am have values ​​close to 0. Although these small effects may be due to chance, they would suggest that these variables are not important or could even be noise for this specific model.

We see that R also offers us the column with the increases in node purity when permuting the variables. In a regression tree, as in our case, it refers to the reduction of variance within the nodes, so it is interpreted in a similar way to the first column.

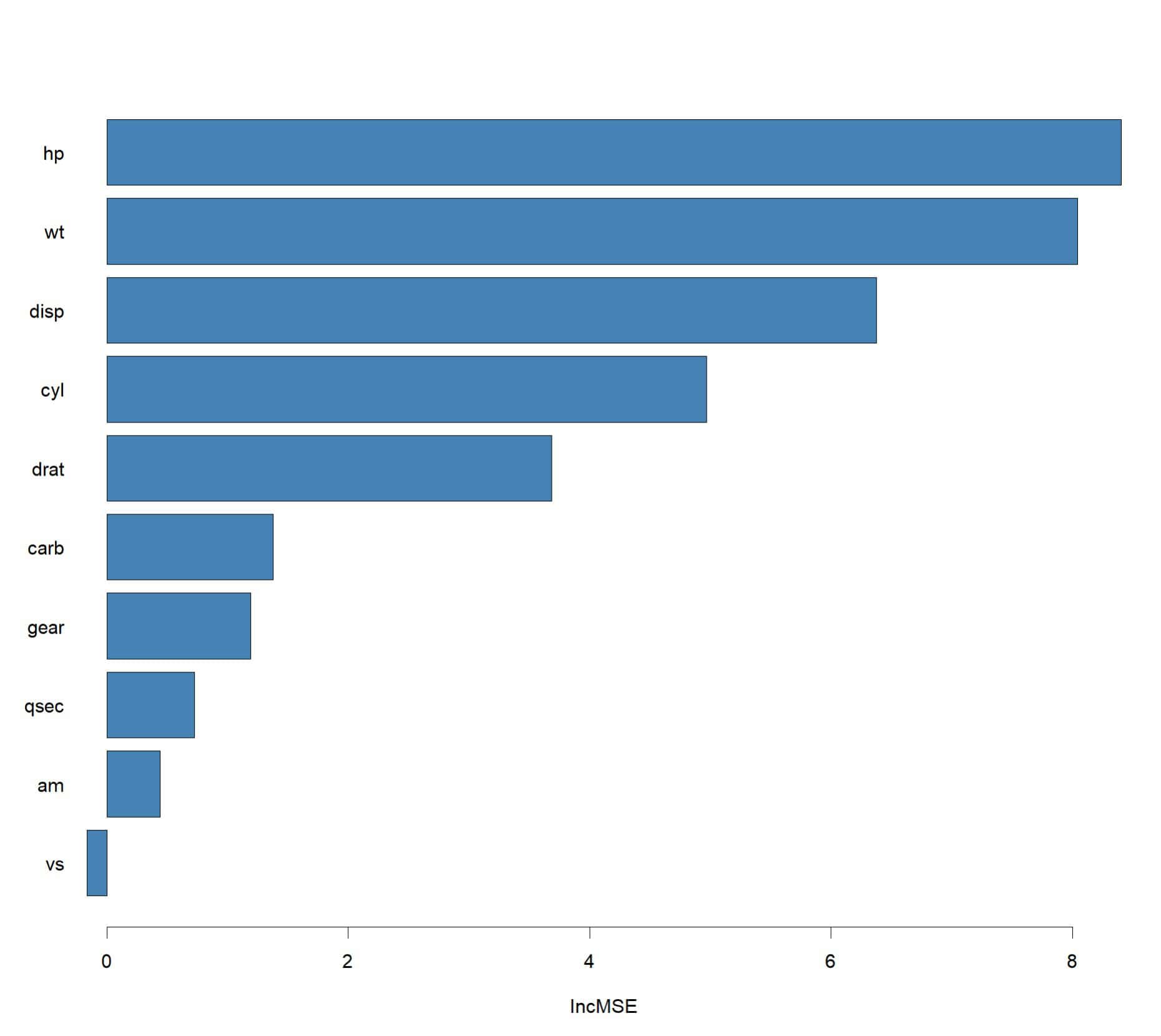
Finally, as you can see in the attached figure, we can graphically represent the importance of the variables. We cannot draw the tree, but this interpretation of the importance of each variable seems to me a good complement to assess the model.

Random forests

We have already seen how bagging is a technique that allows us to reduce the variance of the model and improve its ability to generalize by reducing overfitting. But there is a small flaw that we have not thought of until now.

Suppose there is a variable within the data set that is highly predictive of the target variable of the model. When we build multiple trees using bagging, most of them will use this variable at the highest node of the tree. As a result, all the trees will look quite similar and so will their predictions. To put it as if we knew what we were talking about, the trees would be highly correlated, as would their predictions.

What is the problem? Averaging correlated predictions does not allow for a reduction in variance as large as that which can be achieved if there is no correlation. To solve this problem, random forests were invented.

Random forests go one step further than bagging trees. They do the same resampling to create multiple trees, but in each specific tree, when they reach a node, instead of considering all the predictor variables, they use a random subset of them. A simple rule is to use only the square root of the total number of predictor variables in each node.

For example, if we have a data set with 16 predictor variables, in each node of each tree only 4 are considered, chosen at random, to see which the best candidate is to decide that node. This means that those with the most predictive capacity are no longer obligatorily used and those with less are given a chance. As a result, the trees look less alike, and we alleviate the problem of autocorrelation.

We can make a random forest with R and compare it with the one we made before with bagging. In this case the explained variance is practically the same, 84.6%, although it is more common for it to improve a little compared to that obtained with bagging. You can see the analysis with R in this link.

It may also change the importance of variables somewhat, as some that might not be selected in the bagging context due to their lower relative importance might end up being more influential in some trees. Also, by reducing the correlation between trees, variables that were correlated with others in the bagging model may show a different importance in a random forest.

In any case, reducing the correlation between trees makes the model better able to capture the total variance of the data, thus improving its ability to make predictions with new data.

Boosting the performance of trees

Like bagging, boosting is a set of techniques used in regression and classification to increase the performance of models. In the case of trees, while in bagging and random forests the trees are trained independently and averaged, in boosting the models are trained sequentially and each new tree is built to correct the errors of the previous trees.

The idea, explained in a very simple way, is the following. You start with a very simple tree, with little node depth. From there, the new trees are trained sequentially to correct the residual errors of the previous ones, trying to improve their predictions, adjusting the importance of the variables and the relative weight of each observation. Finally, all the generated trees are combined to make the final prediction, adding the weighted predictions of all the trees (in regression) or by weighted voting (in classification).

Of the three we have seen, this type of approach is the one that has the greatest capacity to reduce both bias and variance compared to simple decision trees.

With these algorithms we enter fully into the world of machine learning, where there are different types of boosting algorithms, from adaptive boosting (AdaBoost) or gradient boosting, to more advanced algorithms such as XGBoost, LightGBM and CatBoost.

Let’s just say that XGBoost is particularly popular for its efficiency and accuracy, and allows the use of regularization techniques to avoid overfitting. LightGBM and CatBoost are alternatives that are designed to improve execution time and better handle data sets with specific characteristics (such as categorical). In any case, we are entering into waters whose depth we are not going to explore in this post.

We’re leaving…

And here we are going to leave the trees for today.

We have seen how bagging techniques (bootstrapping agreggation) allow us to improve the limitations of simple decision trees and how we can go a few steps further to fine-tune the model in that endless fight between bias and variance.

The objective is always the same: to obtain precise predictions but avoiding overfitting so that the model also works with new data, not only with the training data we use to build it.

In any case, don’t think that we have talked about all the trees that we can create or use. For those who love strong emotions, we also have bayesian additive regression trees.

These ensemble decision trees use a non-parametric statistical modelling approach that combines decision tree techniques with bayesian principles. These models have a great capacity to handle complex and non-linear relationships between variables, as well as to provide probabilistic inferences about the predictions. But that’s another story…