Manipulación visual de datos.

La manipulación visual de los datos utilizando gráficos mal diseñados puede distorsionar su interpretación. Se describen los errores más comunes, con el fin de aprender a detectarlos, lo que nos permitirá mejorar la capacidad de análisis visual e interpretación de los datos.
¡Ah, la era de los teléfonos móviles! En algún rincón del mundo, seguro que hay alguien proclamando que su flamante smartphone toma fotos tan buenas como una cámara profesional (o incluso mejores, aunque os cueste creerlo). Y yo, que soy astronauta en mis ratos libres, me pregunto: ¿quién necesita una costosa mirrorless cuando puedes capturar la majestuosidad de la vida con el toque de una pantalla?
En efecto, vivimos en una era donde cualquier teléfono de gama alta promete fotos dignas de un profesional. Los fabricantes se vanaglorian de sus increíbles algoritmos, cámaras múltiples y millones de megapíxeles, pero, cuando vemos el resultado de cerca, no todo es tan perfecto como parece.
Las fotos pueden tener una apariencia impecable en la pantalla del móvil, pero al hacer zoom o compararlas con las de una cámara profesional, los defectos emergen. ¿Qué pasa entonces con esos detallitos técnicos que los móviles supuestamente dominan?
Me pregunto si la magia del software, los megapíxeles infinitos y esa inteligencia artificial que promete convertir cada selfie en una obra de arte se corresponden con una verdad tangible. ¿O será que estamos siendo engañados por el brillo y el glamour del marketing?
Y aquí es donde las cosas se ponen interesantes, porque esta ilusión fotográfica nos lleva de la mano a un tema igual de intrigante: la manipulación visual de los datos en estadística. Al igual que con las fotos de nuestros móviles, los gráficos pueden parecer impresionantes y convincentes a simple vista, dando la sensación de precisión y calidad.
Pero una mirada más profunda puede revelar las trampas y errores que acaso distorsionen nuestra comprensión, ocultando verdades importantes. Un gráfico, que parece sencillo y directo, puede estar maquillando los datos, exagerando diferencias mínimas o distorsionando la escala para hacer que algo insignificante parezca crítico.
Si seguís leyendo esta entrada, aprenderéis a reconocer algunas de las trampas más comunes en la interpretación visual de gráficos, lo que os ayudará a ver «más allá de la imagen», tal como haríais con una foto demasiado retocada.
Sin cero, no hay verdad
Una de las trampas más frecuentes es someter los ejes, sobre todo el horizontal, a un efecto perverso de la gravedad, de forma que la escala del eje de ordenadas (el eje y) no empieza en cero y, lo más habitual, el eje x flota hacia los cielos del diagrama.
Esto suele verse con gráficos de barras que, a primera vista, parecen mostrarnos, de manera inocente, enormes diferencias entre las categorías comparadas, como vemos en el gráfico de la izquierda de la primera figura. Sin embargo, si lo observamos con atención, vemos que el eje ha sido recortado, saltándose el cero, amplificando las diferencias de manera engañosa.
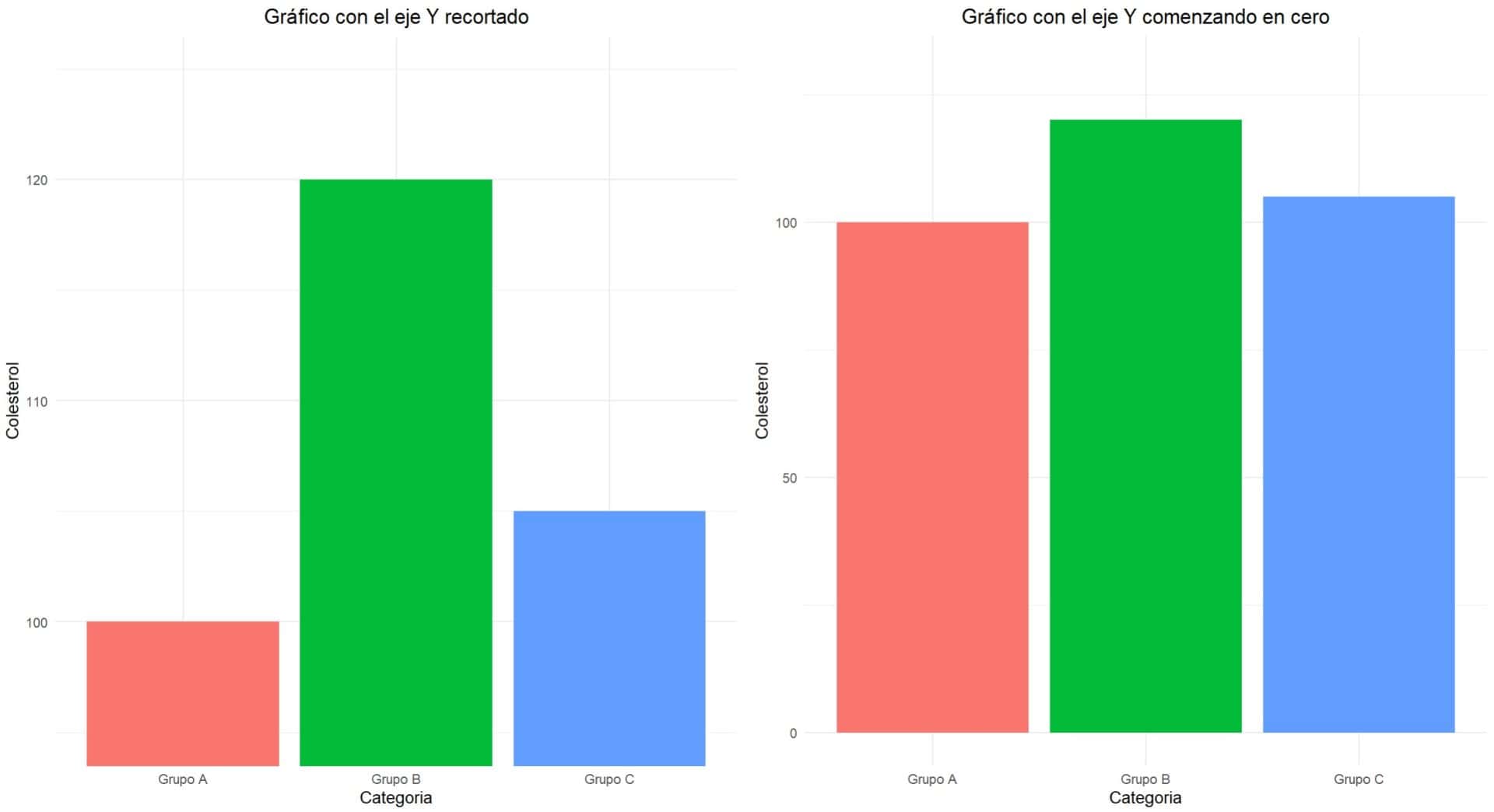
Si el gráfico comenzase en cero, como vemos en el de la derecha, las diferencias parecerían mucho menos dramáticas que en el gráfico recortado. Aquellos de vosotros que seáis malpensados, no podréis evitar llegar a la conclusión de que el autor del gráfico ha intentado hacernos creer que la diferencia es mucho más importante de lo que realmente es.
Así que aquí aprendemos una primera lección: debemos verificar siempre que los ejes del gráfico comienzan en el origen de coordenadas y, si no es así, preguntarnos si la diferencia que se muestra es realmente tan importante como aparenta.
Cuando la tarta se vuelve indigerible
El diagrama de sectores, nuestra querida tarta, es también víctima frecuente de autores tramposos.
Los gráficos circulares son un recurso visual popular por su apariencia ordenada y colorida. Sin embargo, cuando hay más de unas pocas categorías, estos gráficos pueden volverse increíblemente difíciles de leer.
Nuestros limitados cerebros no están bien entrenados para comparar áreas curvas, lo que significa que pequeñas diferencias entre porciones del gráfico pueden pasar desapercibidas o parecer más grandes de lo que son.
Imaginad un gráfico circular que muestra 10 categorías, todas en colores brillantes, como el de la izquierda de la figura adjunta. ¿Podéis realmente apreciar con precisión cuál es la más grande? Probablemente no. Si dos segmentos son similares en tamaño, identificar cuál es mayor puede volverse un ejercicio frustrante.
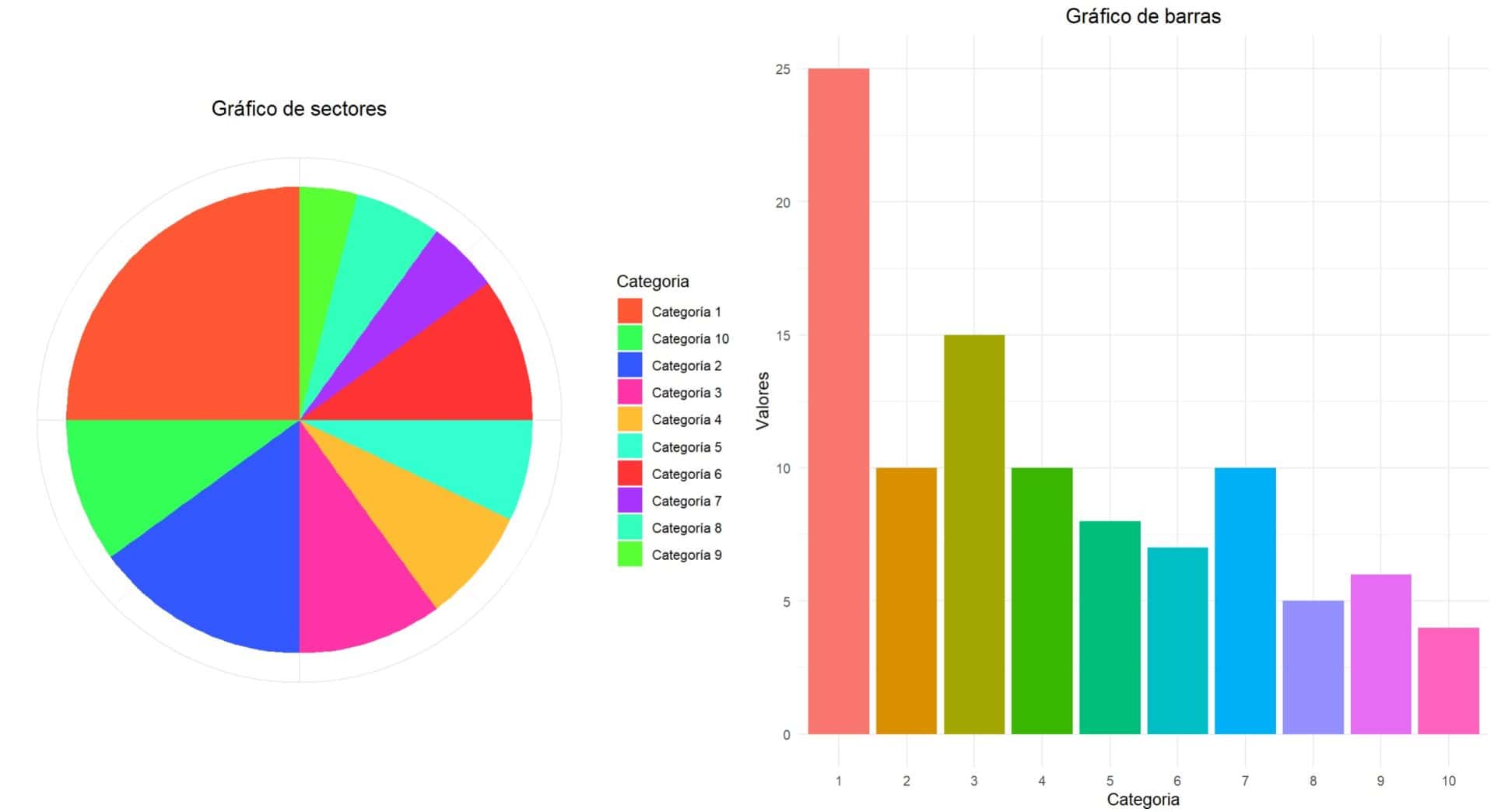
En estos casos, será siempre mejor utilizar un gráfico de barras, con el que será más fácil hacer las comparaciones entre las diferentes categorías, tal como veis en el gráfico de la derecha. Eso sí, sin hacer trampas con los ejes, como ya sabemos.
Ajustando la realidad a golpe de regla
Otro recurso muy socorrido es la manipulación del escalado de los ejes, usando escalas que no se ajustan bien a los datos presentados.
Por ejemplo, se pueden emplear escalas logarítmicas (donde los valores se comprimen) para que los cambios grandes parezcan menores. Esto puede ser útil en algunos contextos científicos, pero si se aplica sin aclaración, puede inducir a error si se mira el gráfico de manera superficial.
Imaginad una empresa farmacéutica que ha hecho un estudio con un fármaco nuevo para el tratamiento de esa grave enfermedad que es la fildulastrosis, dándole su fármaco a los 1000 participantes del grupo A y el tratamiento habitual a los 1000 del grupo B. Una vez que consigue demostrar que el fármaco nuevo es no-inferior al habitual, estudia sus efectos sobre la duración del ingreso en el hospital, midiendo el número de pacientes que permanecen ingresados a lo largo de los 10 primeros días de tratamiento.
Estos resultados nos los muestran en el gráfico de la izquierda de la siguiente figura.
A simple vista, podemos ver que hay pocas diferencias en el número de ingresados al final del periodo en ambas ramas del ensayo. Aunque el descenso es algo mayor en el grupo B, ambos bajan poco y la diferencia entre los dos grupos parece ser insignificante.
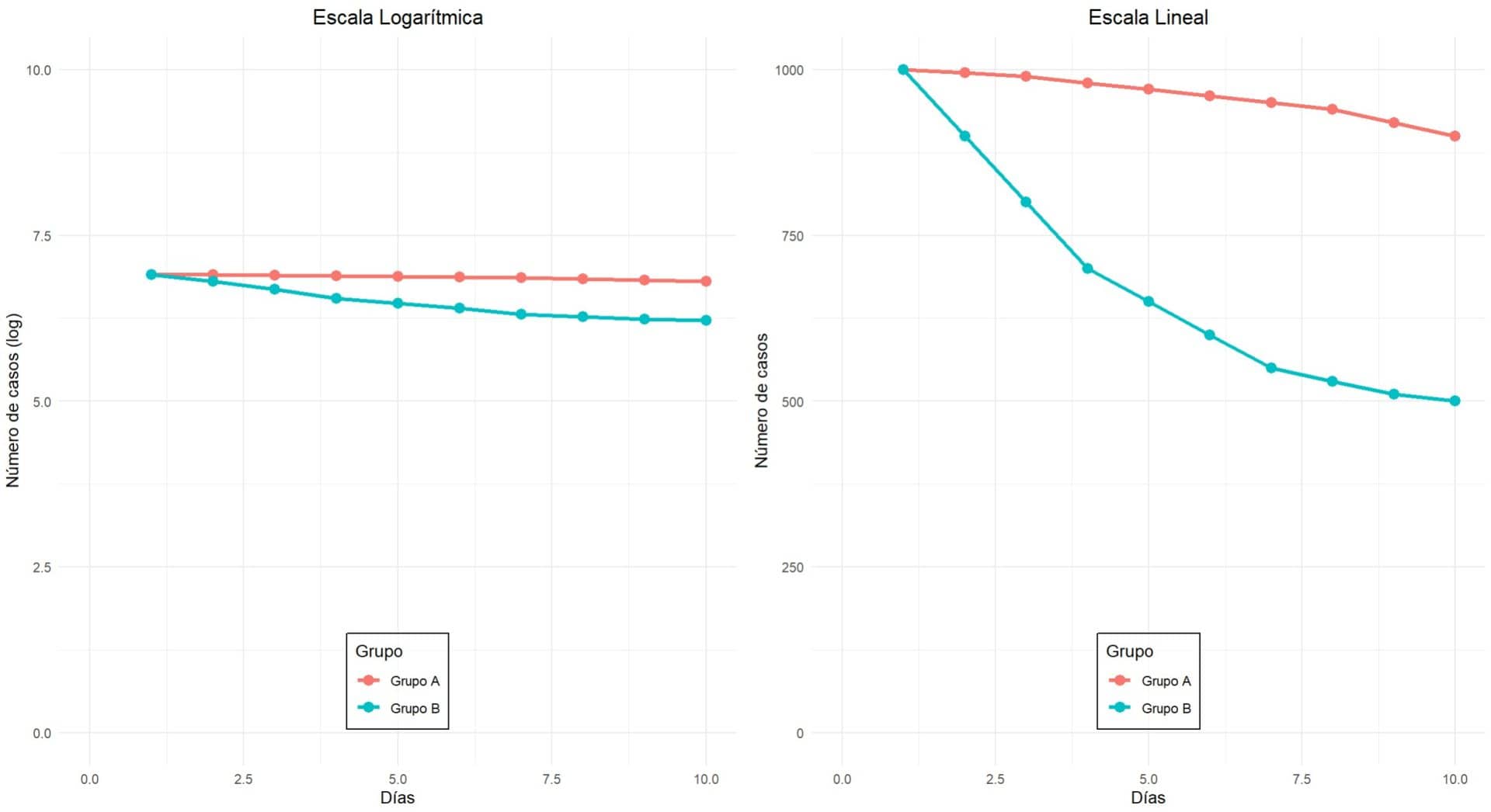
Pero si nos fijamos un poco, nos daremos cuenta de que la escala del eje y tiene una transformación logarítmica. ¿Por qué lo habrán hecho? Yo diría que el tipo de datos representados no hace necesaria esta transformación.
En la parte de la derecha os muestro el mismo gráfico, pero con ambos ejes en escala lineal. Con un simple vistazo vemos que la interpretación es bien diferente. Mientras que en el grupo A se produce una leve reducción del 10% en el número de pacientes ingresados, esta es del 50% en el grupo B del tratamiento habitual. Aquí sí que parece que hay una diferencia relevante entre los dos tratamientos, a favor del habitual.
En resumen, la lección que aprendemos de este ejemplo es que siempre tendremos que valorar la idoneidad de utilizar una transformación de la escala de los ejes. Las escalas logarítmicas no distribuyen los valores de manera uniforme, sino que comprimen los grandes cambios para que visualmente las diferencias parezcan más pequeñas de lo que realmente son.
Cuando lo que falta es lo que engaña
Otra forma de engaño con los gráficos es omitir deliberadamente el contexto de los datos que se representan. Tal como una foto espectacular puede engañarte sobre la belleza de un lugar (sin mostrarte que hay una fábrica contaminante justo fuera del encuadre de la foto), los gráficos que no incluyen toda la información pueden llevarte a conclusiones erróneas.
Imaginad que se presenta un gráfico que muestra una reducción significativa en las tasas de mortalidad de pacientes tratados con un nuevo medicamento para la fildulastrosis, tal como se muestra en el diagrama de la izquierda de la siguiente figura. El gráfico muestra que la mortalidad disminuyó del 45% al 30% en los últimos cinco años, lo que parece un avance notable.
Sin embargo, lo que los autores se olvidan de mostrar es que, durante ese mismo periodo de tiempo, las mejoras en la atención médica general y la introducción de nuevos procedimientos no relacionados con el medicamento también redujeron las tasas de mortalidad en todas las series de pacientes publicadas, incluso en aquellos no tratados con el fármaco en cuestión.
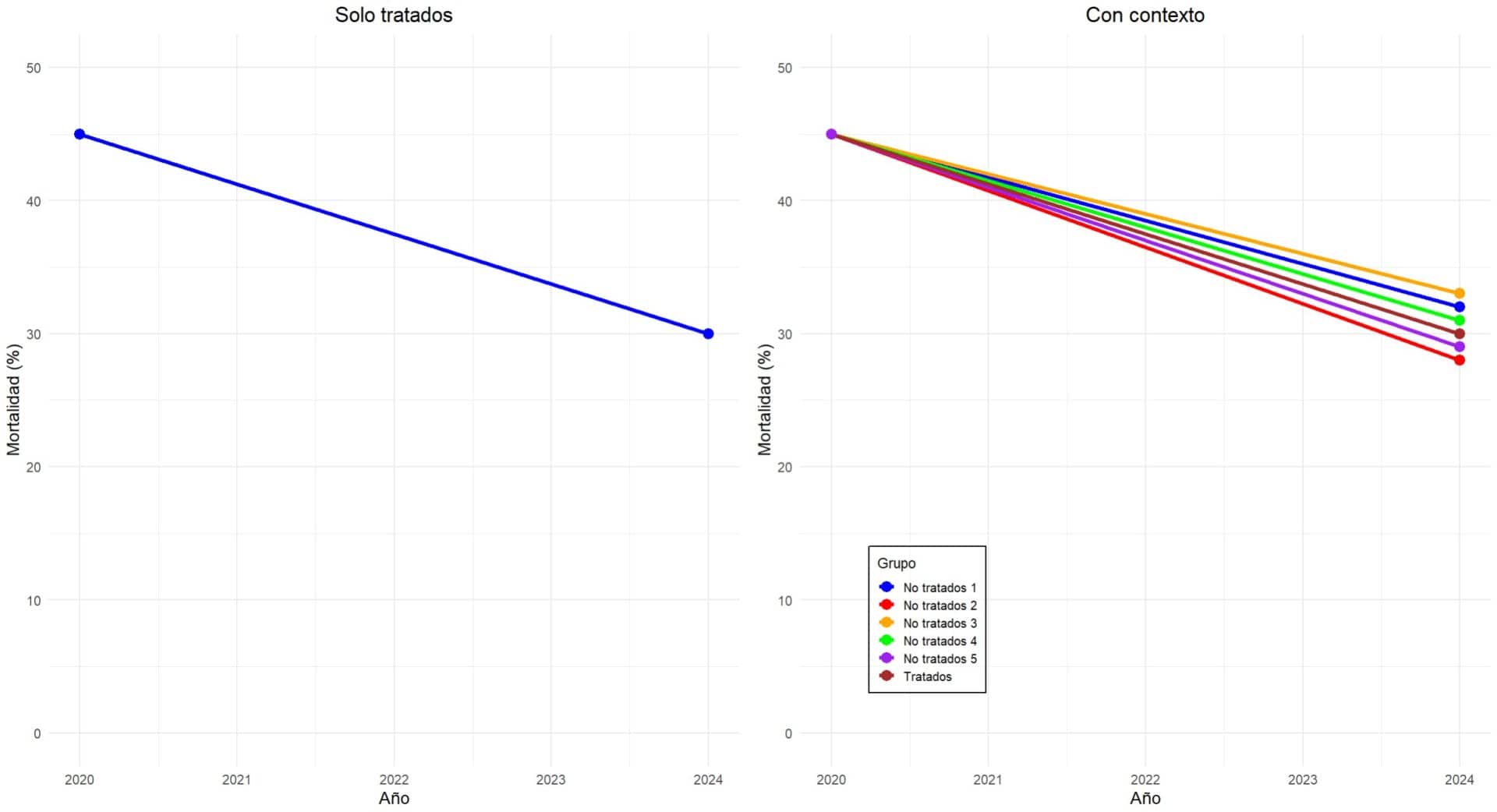
Si el gráfico incluyera el contexto de los avances generales en el tratamiento, quedaría claro que la reducción en la mortalidad no es solo gracias al fármaco. El contexto faltante crea la falsa impresión de que el medicamento es la única causa de esta mejora, cuando en realidad, otros factores también jugaron un papel importante.
Moraleja, valorad siempre si el gráfico aporta toda la información necesaria para calibrar la importancia del efecto que quiere demostrar, no vaya a ser que estén intentando sobrevalorar la intervención.
Cuando los ejes faltan, las conclusiones bailan
Otro truco común es ocultar o modificar los ejes de un gráfico de forma que los datos presenten una imagen distorsionada. Los gráficos de dispersión o de líneas, en particular, pueden mostrar «tendencias» que en realidad no existen si los ejes no están rotulados adecuadamente o se omiten ciertas unidades.
Volviendo a nuestro pérfido laboratorio farmacéutico, vamos a imaginar que, esta vez, nos presenta un gráfico de líneas para demostrar la efectividad de un nuevo medicamento que reduce los niveles de colesterol en sangre, tal como veis en el gráfico de la izquierda de la siguiente figura.
Este gráfico muestra una caída drástica de los niveles de colesterol entre las personas que lo tomaron durante 6 meses. Pero fijaos en un detalle: el eje y no está rotulado: faltan las etiquetas, las unidades de medida, no sabemos qué intervalo de valores comprende… ¿Por qué lo han habrán hecho así?
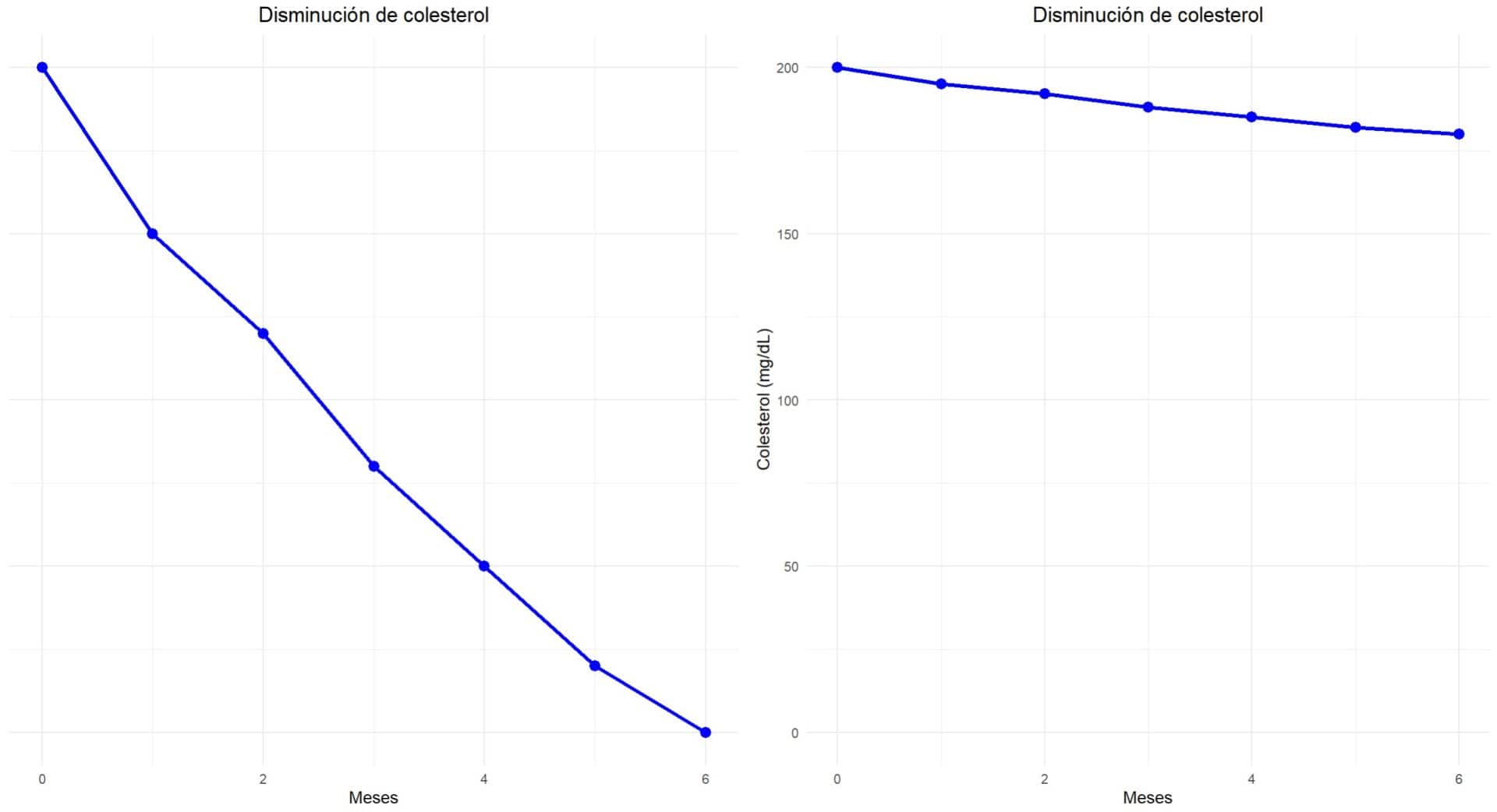
La respuesta está en el gráfico de la derecha, elaborado con los mismos datos de colesterolemia. Además de comenzar en los 180 mg/dl en lugar de en cero, vemos que la caída de valores va desde los 200 mg/dl hasta 180 mg/dl. Ya no nos parece tan drástica y comprendemos en seguida lo que se persigue al omitir los rótulos del eje.
Este ejemplo nos enseña que la manipulación o falta de claridad en los ejes puede inducir a errores en la interpretación del gráfico. Sin ejes bien rotulados, es fácil caer en la trampa visual que exagera los resultados.
Cuando los excesos visuales confunden
Para ir terminando, nos referiremos a aquellas situaciones en las que hay un verdadero abuso de los recursos visuales, tales como efectos en 3D, gran diversidad de colores y formas, sombras, etc., todo ello favorecido y posibilitado por la potencia de los programas gráficos disponibles en la actualidad.
Al igual que los filtros de Instagram pueden hacer que una foto normal parezca una obra maestra (o, en otras ocasiones, un esperpéntico desastre), el uso excesivo de colores y efectos en los gráficos puede distraer y confundir más que ayudar. Los gráficos con demasiados colores o con un uso innecesario de sombras, degradados y texturas pueden dificultar la interpretación y dar una sensación de caos.
Una recomendación sabia puede ser la de usar colores sobrios y consistentes en los gráficos. Si se necesita comparar varias categorías, elegiremos una paleta de colores limitada que facilite la comparación.
Nos vamos…
Y con esto vamos a ir finalizando esta entrada tan tramposa.
Hemos visto algunos de los malos usos de los gráficos que, por desconocimiento de su uso o por intenciones inconfesables, pueden transmitirnos una información que no se corresponde con la real que aportan los datos con los que se elabora el gráfico.
Será bueno seguir una serie de pasos como verificar los ejes y escalas de los gráficos, desconfiar de los gráficos que omiten contextos importantes o parecen demasiado adornados y preferir gráficos de barras o líneas sobre gráficos circulares o de tarta para comparaciones precisas.
Al igual que cuando hablamos de fotografía, la belleza de los números está en su claridad, no en su brillo superficial. Y recordad la frase de Susan Sontag: que las fotografías sean a menudo elogiadas por su veracidad, su honradez, indica que la mayor parte de las fotografía, desde luego, no son veraces. Fijaos siempre en los datos, no solo en el gráfico.
Y ahora sí que nos vamos. No hemos hablado nada de otro error que se puede cometer al elaborar un gráfico, como recurrir al gráfico inadecuado para el tipo de variable que queremos representar y confundir las tartas con las barras o las barras con los histogramas, por poner algunos ejemplos. Pero esa es otra historia…
