Cálculo de valores esperados.

El cálculo de valores esperados se realiza multiplicando los marginales de la celda y dividiendo por el total de la tabla. Se razona esta regla.

¿Recordáis la pasada entrada en la que hablábamos de chicas estudiantes con hábitos nocivos para la salud?. Para aquellos de memoria floja, hagamos un breve recordatorio.

Resulta que entrevistábamos a 585 chicas y averiguábamos su nivel de estudios y si bebían, fumaban, ambas cosas o ninguna. Con los resultados construíamos la tabla de contingencia que os vuelvo a mostrar aquí.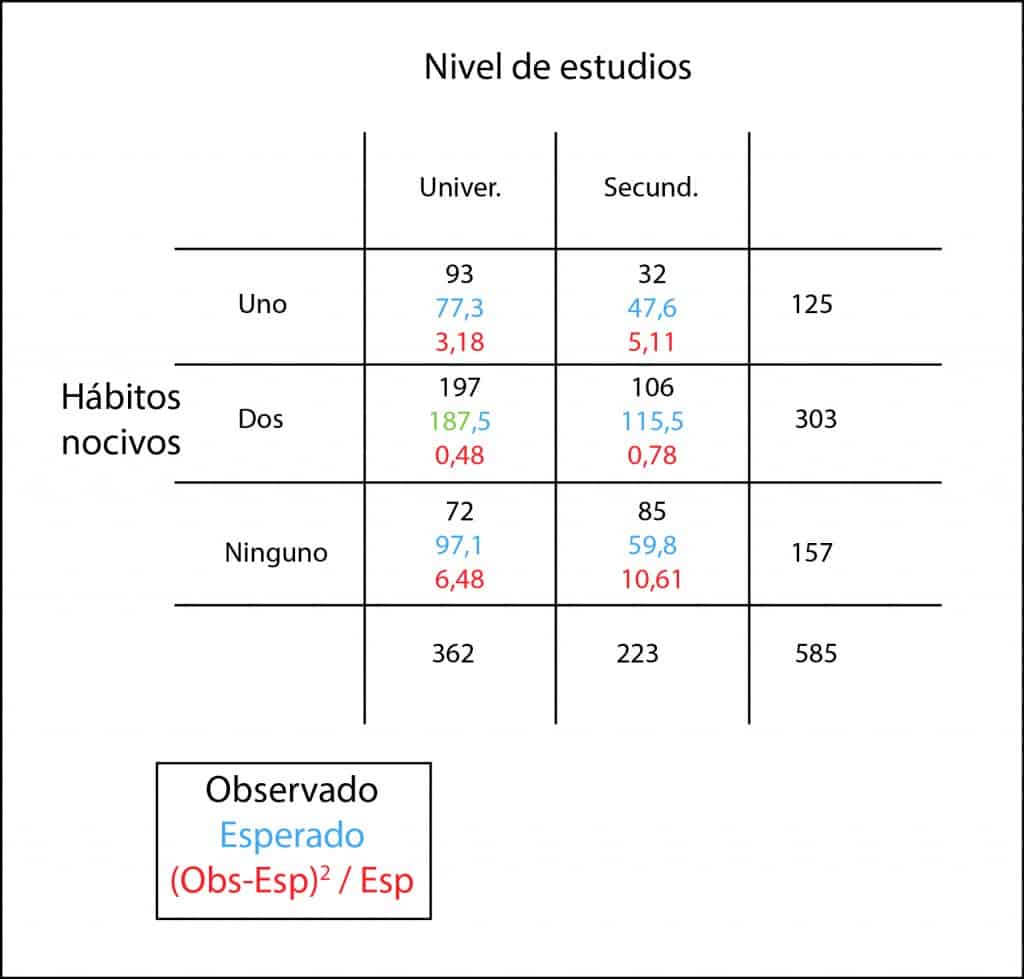

Nosotros queríamos saber si había alguna relación entre el nivel de estudios y el tener hábitos nocivos, para lo cual empezábamos por establecer nuestra hipótesis nula de que ambas variables cualitativas eran independientes.

Así que procedíamos a realizar una prueba de la ji cuadrado para llegar a una conclusión. Lo primero que teníamos que hacer era calcular los valores esperados de cada celda, cosa que es muy sencilla, ya que solo hay que multiplicar el total de la fila por el total de la columna y dividirlo por el total de la tabla… Alto! ¿Y por qué?. ¿De dónde sale esta regla?. ¿Sabéis por qué ese producto dividido por el total equivale al número esperado de esa celda?. Está bien tener reglas que nos faciliten las tareas, pero a mí me gusta saber de dónde salen las cosas y seguro que pocos os habéis parado a pensarlo. Vamos a verlo.

Cálculo de valores esperados

Partimos de la base de que vamos a razonar bajo el supuesto de la hipótesis nula de que las variables hábito nocivo y nivel de estudios son independientes. Vamos a calcular el valor esperado de la celda que corresponde a las estudiantes de secundaria con dos hábitos nocivos.

Como ambas situaciones (haber estudiado hasta secundaria y fumar y beber) son independientes, la probabilidad de que las dos ocurran será igual a la probabilidad de una por la probabilidad de la otra:

P(secundaria y dos hábitos) = P(secundaria) x P(dos hábitos)

Sabemos que P(secundaria) será igual al número total de chicas con nivel de secundaria dividido por el total de entrevistadas. Igualmente, P(dos hábitos) será igual a todas las que beben y fuman dividido por el total de entrevistadas (el total de la tabla). Si sustituimos la expresión anterior por sus valores, obtenemos:

P(secundaria y dos hábitos) = (223/585) x (303/585)

Ya sabemos cuál es la probabilidad de cada una de pertenecer a esa celda. ¿Cuál es el número esperado?. Pues muy sencillo, la probabilidad de cada una multiplicado por el número total de chicas entrevistadas:

P(secundaria y dos hábitos) = 585 x (223/585) x (303/585)

Y si anulamos los 585 de numerador y denominador y simplificamos la expresión, nos quedará:

P(secundaria y dos hábitos) = (223 x 303) / 585

Que no es otra cosa que el marginal de la fila por el marginal de la columna y dividido por el total de la tabla y cuyo resultado, en nuestro ejemplo, es de 115,5.

Nos vamos…

Veis, pues, de donde sale la regla para calcular el número de ocurrencias esperadas en una tabla de contingencia. Claro que ya sabéis que para averiguar si son o no variables independientes todavía quedaría estandarizar los cuadrados de las diferencias, calcular la suma y obtener su probabilidad según la distribución de la ji cuadrado. Pero esa es otra historia…