Análisis de la varianza (ANOVA).

El análisis de la varianza (ANOVA) es la técnica que sirve para comparar las diferencias entre más de dos medias de una variable cuantitativa.

Al menos cuando hablamos de contraste de medias.

Supongamos que queremos saber si una población de esquimales come una cantidad de carne de foca superior a un valor determinado. Podemos calcular la media en la muestra, estimar su intervalo de confianza en la población y ver si incluye o no dicho valor.

Supongamos ahora que tenemos dos poblaciones de esquimales y queremos saber si hay diferencia en su consumo de carne de foca. No tenemos más que calcular las medias y hacer una sencilla prueba de la t de Student para comparar sus medias. También podríamos calcular sus intervalos de confianza y ver si hay solapamiento.

Análisis de la varianza (ANOVA)

Pero, ¿qué pasa si tenemos tres o más poblaciones?. Pues que no nos vale ni la t de Student ni la comparación de intervalos. En estos casos tenemos que utilizar una técnica que tiene el engañoso nombre de análisis de la varianza (ANOVA, de sus siglas en inglés). Y digo engañoso nombre porque lo que se comparan son medias, no varianzas. Eso sí, para compararlas utilizamos la forma en la que varían los datos, siguiendo un razonamiento bastante ingenioso. Vamos a tratar de explicarlo ayudándonos de un ejemplo de la vida real.

Como en un chiste de mi infancia, tenemos cinco franceses, cinco españoles y cinco italianos (en los chistes suele haber un francés, un italiano y un español, pero poca varianza podríamos analizar con tan poca gente). A estas 15 personas les preguntamos cuántos litros de vino se beben al mes, obteniendo la distribución que veis en la tabla.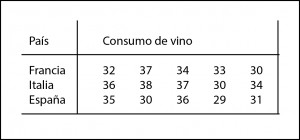

Si calculamos los valores medios de cada grupo veremos que los franceses beben 33,2 litros al mes, los italianos 35 y los españoles 32,2. ¿Quiere esto decir que en Italia son más borrachos que en Francia y en Francia más que en España?.

Pues solo con las medias no podemos saberlo. Aunque las muestras que hemos escogido fuesen representativas de sus poblaciones, siempre cabe la posibilidad de que las diferencias se deban al más puro azar. Así que, como siempre, tenemos que hacer un contraste de hipótesis para poder averiguarlo.

Como primer paso establecemos la hipótesis nula de que no existen diferencias reales entre los tres grupos y que las diferencias observadas se deben al azar. La hipótesis alternativa, por su parte, dice que sí hay diferencias entre los tres grupos. Así que, bajo la asunción de la hipótesis nula, vamos a hacer el análisis de la varianza de un factor, que sería el país de procedencia.

Descomponiendo la varianza

El consumo de vino medio de nuestros 15 borrachos es de 33,5 litros al mes. Suponiendo cierta la hipótesis nula, si tomamos uno al azar, de cualquier país, el consumo esperado sería de 33,5. Sin embargo, es fácil de entender que la mayor parte de los sujetos extraídos al azar tendrán un valor diferente a la media esperada. El valor de ese individuo lo podemos descomponer en tres partes: la media, la variación debida al país de procedencia y la variación debida al azar. Si me permitís una formulita, sería la siguiente:

x = media + efecto del país + efecto del error aleatorio

Si la hipótesis nula es cierta y no hay diferencias entre grupos, la variación debida al país será muy pequeña (similar a la del azar), mientras que si es falsa, esta variación será mayor. Pensad ahora en el valor del cociente país/error aleatorio. Si no hay diferencias debidas al grupo (la hipótesis nula es cierta), el cociente valdrá 1 o menos de 1. Si los grupos tienen medias diferentes, el cociente valdrá más de 1, tanto más cuánto mayores sean las diferencias entre grupos, ya que el error aleatorio será siempre más o menos el mismo.

Pues bien, ya casi lo tenemos. Sabemos que la varianza es la suma media de los cuadrados de la distancia de cada valor respecto de la media. Recordad que se elevaban al cuadrado estas distancias para que las negativas no se anulasen con las positivas.

Esta varianza puede descomponerse en los dos componentes que hemos explicado: el debido a la varianza entre grupos, llamado suma de cuadrados, y el debido al azar, llamado residual de cuadrados:

Suma total de cuadrados = suma de cuadrados por grupo + residual de cuadrados.

La suma de cuadrados

No os voy a poner las fórmulas para calcular estas sumas de cuadrados, aunque no son muy complejas y un ejemplo como el que estamos viendo puede resolverse perfectamente con una sencilla calculadora. No merece la pena complicarse la vida. Cualquier programa de estadística calcula estas sumas de cuadrados sin esfuerzo.

Y una vez que tenemos las sumas de cuadrados es donde aparece la magia de los números, porque da la casualidad de que el cociente de los cuadrados partido por los residuales (país/aleatorio) sigue una distribución de probabilidad conocida, que no es otra que una F de Snedecor con grupos-1, n-grupos grados de libertad.

Si lo calculamos (yo lo he hecho empleando el comando aov del programa R), obtenemos una F de 1,14. La probabilidad de obtener este valor de F con estos grados de libertad es de 0,35. Como es mayor de 0,05, no podemos rechazar la hipótesis nula, así que no nos queda más remedio que asumir que franceses, italianos y españoles somos igual de borrachos.

Nos vamos…

Solo un par de comentarios más antes de terminar. Primero, para poder hacer este tipo de análisis deben cumplirse tres circunstancias: las muestras deben ser independientes, deben seguir una distribución normal y deben tener varianzas iguales (lo que se conoce con el simpático nombre de homocedasticidad). Nosotros hemos asumido las tres condiciones.

Segundo, si hubiésemos obtenido una F con p<0,05 y hubiésemos rechazado la hipótesis nula habríamos podido decir que había diferencias en los consumos de vino pero, ¿entre qué grupos?. Lo primero que se nos pasa por la cabeza es tomar los grupos de dos en dos y hacer el contraste con dos medias, pero esto no se puede hacer así sin más. Cuántas más parejas comparemos, más probable es que cometamos un error de tipo I y encontremos una diferencia significativa por puro azar, ya que la significación global varía al comparar las medias dos a dos.

Para hacerlo tendríamos que utilizar otras técnicas que tienen en cuenta este efecto, como la de Bonferroni o la de Tukey. Pero esa es otra historia…