Estandarización.

Se describe la estandarización, que consiste en restar la media a un valor y dividirlo por su desviación estándar.

Pero no me vale una barra cualquiera. Tiene que ser una barra muy especial. O mejor, una serie de barras. Y no estoy pensando en un diagrama de barras, tan conocidos y utilizados que cuando abres el PowerPoint casi te hace uno sin que se lo pidas. No, estos diagramas son muy insulsos, solo representan cuántas veces se repite cada uno de los valores de una variable cualitativa, pero no nos dicen nada más.

Histograma y densidad de probabilidad

Yo estoy pensando en un diagrama mucho más profundo. Me refiero al histograma. ¡Vaya!, me diréis, pues no es otro diagrama de barras. Sí, pero de otra clase de barras, mucho más informativas. Para empezar, el histograma se utiliza (o debería) para representar frecuencias de variables cuantitativas continuas. El histograma no es un diagrama de barras, sino una distribución de frecuencias. ¿Y eso qué significa?. Pues que las barras, en el fondo, son algo artificial.

Supongamos una variable cuantitativa continua como puede ser el peso. Imaginemos que el rango de nuestra distribución va de 38 a 118 kg de peso. En teoría, podemos tener infinitos valores de peso (como con cualquier variable continua), pero para representar la distribución dividimos el rango en un número de intervalos arbitrario y dibujamos una barra para cada intervalo cuya altura (y, por tanto, superficie) sea proporcional al número de casos del intervalo. Eso es un histograma: la distribución de frecuencias.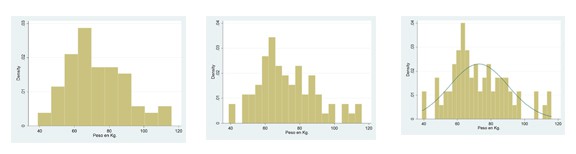

Ahora supongamos que hacemos los intervalos cada vez más estrechos. El perfil que forman las barras se irá pareciendo cada vez más a una curva según se estrechen los intervalos.

Al final, lo que tendremos será una curva que se llama curva de densidad de probabilidad. La probabilidad de un determinado valor será cero (uno pensaría que debería ser la altura de la curva en ese punto, pero resulta que no, que es cero), pero la probabilidad de los valores de un determinado intervalo será igual a la superficie del área bajo la curva en ese intervalo. Y, ¿cuál será el área bajo toda la curva?. Pues fácil: la probabilidad de encontrar cualquier valor, o sea, uno (100% para los amigos del porciento).

Veis, pues, que el histograma es mucho más de lo que parece. Nos dice que la probabilidad de encontrar un valor inferior a la media es 0,5, pero no solo eso, sino que podemos calcular la densidad de probabilidad de cualquier valor utilizando una formulita que prefiero no poner porque cerraríais  el navegador y dejaríais de leer esta entrada. Además, hay una forma de solucionarlo algo más simple.

Con las variables que siguen una distribución normal (la famosa campana) la solución es sencilla. Sabemos que una distribución normal se define perfectamente por su media y su desviación estándar.

El problema es que cada distribución tiene las suyas, con lo que la densidad de probabilidad también es específica de cada distribución. ¿Qué hacemos?. Pues nos inventamos una distribución normal estándar de media cero y desviación típica 1 y nos estudiamos su densidad de probabilidad de tal forma que no necesitemos fórmulas ni tablas para conocer la probabilidad de un segmento determinado.

Estandarización

Una vez hecho esto, tomamos cualquier valor de nuestra distribución y los transformamos en su alma gemela de la distribución estándar. A este proceso se le denomina estandarización y es tan sencillo como restar al valor la media y dividirlo por la desviación típica. Así obtenemos otro de los estadísticos que los médicos en general, y los pediatras en particular, veneramos más profundamente: el z score.

Las probabilidades de la distribución estándar son bien conocidas. Un z de cero está en la media. El intervalo de z = 0 ± 1,64 engloba el 90% de la distribución, el z = 0 ± 1,96 el 95%, y el z = 0 ± 2,58 el 99%. Lo que se hace, en la práctica, es determinar el z deseable para la variable que medimos, una vez estandarizada. Este valor suele ser ±1 ó ± 2, según lo que midamos. Además, podemos comparar cómo se modifica el z en determinaciones sucesivas.

El problema surge porque en medicina hay muchas variables cuya distribución se encuentra sesgada y no se ajusta a una distribución normal, como es el caso de la talla, el colesterol sanguíneo y muchas otras. Pero no desesperéis, para eso los matemáticos se han inventado una cosa que llaman el teorema central del límite, que viene a decir que si el tamaño de la muestra es lo suficientemente grande podemos estandarizar cualquier distribución y enlazarla con la distribución normal estándar. Este teorema es una cosa estupenda, ya que permite estandarizar incluso para variables no continuas que siguen otro tipo de distribuciones como la binomial, la de Poisson u otras.

Nos vamos…

Pero la cosa no queda aquí. La estandarización es la base para calcular otras características de la distribución, como su índice de asimetría o su curtosis, y está además en la base de muchas pruebas de contraste de hipótesis que buscan estadísticos de distribución conocida para calcular la significación, pero esa es otra historia…