Lectura crítica del metanálisis de pruebas diagnósticas.

Se describe la metodología del metanálisis de pruebas diagnósticas, sus sesgos característicos, sus parámetros y las bases para su lectura crítica.
El genio al que me estoy refiriendo en el título de esta entrada no es otro que Alan Mathison Turing, considerado uno de los padres de la ciencia de la computación y un precursor de la informática moderna.
Para los matemáticos, Turing es más conocido por su implicación en la solución del problema de decisión propuesto previamente por Gottfried Wilhelm Leibniz y David Hilbert, que buscaba poder definir un método que pudiese aplicarse a cualquier sentencia matemática para saber si esa sentencia era cierta o no (para el que le interese, se pudo demostrar que tal método no existe).
Pero la fama actual de Turing entre el gran público le viene gracias al cine y a sus trabajos en estadística durante la II Guerra Mundial. Y es que a Turing le dio por explotar la magia bayesiana para profundizar en el concepto de cómo la evidencia que vamos recogiendo durante una investigación puede apoyar la hipótesis de trabajo de partida o no hacerlo, favoreciendo entonces el desarrollo de una nueva hipótesis alternativa.
Esto le permitió descifrar el código de la máquina Enigma, que era la que utilizaban los marinos de guerra alemanes para cifrar sus mensajes, y que es la historia que se ha llevado al cine. Esta línea de trabajo condujo al desarrollo de conceptos como el de peso de la evidencia y de los conceptos de verosimilitud, con los que se podían confrontar hipótesis nulas y alternativas, que se aplicaron en biomedicina e hicieron posible el desarrollo de nuevas formas de valorar pruebas diagnósticas, tal como las que vamos a tratar hoy.
Y es que toda esta historia sobre Alan Turing no es más que un reconocimiento a una de las personas cuya contribución hizo posible que después se desarrollara el diseño metodológico del que vamos a hablar hoy, que no es otro que el metanálisis de pruebas diagnósticas.
Ya sabemos que un metanálisis es un método de síntesis cuantitativa que se utiliza en las revisiones sistemáticas para integrar los resultados de los estudios primarios en una medida resumen de resultado. Lo más habitual es encontrarse con revisiones sistemáticas sobre tratamiento, para las cuales está bastante bien definida la metodología de realización y la elección de la medida resumen de resultado. Menos habituales, aunque cada día más, son las revisiones sobre pruebas diagnósticas, que han sido posibles tras el desarrollo y caracterización de los parámetros que miden la potencia diagnóstica de una prueba.
El proceso de realización de una revisión sistemática de diagnóstico sigue esencialmente las mismas pautas que el de una revisión de tratamiento, aunque hay algunas diferencias específicas que trataremos de aclarar. Nos centraremos en primer lugar en la elección de la medida de resultado y trataremos de tener en cuenta el resto de las peculiaridades cuando demos algunas recomendaciones para realizar la lectura crítica de estos trabajos.
Características del metanálisis de pruebas diagnósticas
Al elegir la medida de resultado nos encontramos con la primera gran diferencia con los metanálisis de tratamiento. En el metanálisis de pruebas diagnósticas (MAD) la forma más frecuente de valorar la prueba es combinar la sensibilidad y la especificidad como valores resumen.
Sin embargo, estos indicadores presentan un problema y es que los puntos de corte para considerar los resultados de la prueba como positivos o negativos suelen variar entre los distintos estudios primarios de la revisión. Además, en algunos casos la positividad puede depender de la objetividad del evaluador (pensemos en los resultados de pruebas de imagen). Todo esto, además de ser una fuente de heterogeneidad entre los estudios primarios, constituye el origen de un sesgo típico del MAD denominado efecto umbral, en el que nos detendremos un poco más adelante.
Por este motivo a muchos autores no les gusta emplear sensibilidad y especificidad como medidas resumen y recurren a los cocientes de verosimilitud o cocientes de probabilidad, positivo y negativo. Estos cocientes tienen dos ventajas. La primera, son más robustos frente a la presencia de efecto umbral. La segunda, como ya sabemos, permiten calcular la probabilidad postprueba, ya sea usando la regla de Bayes (odd preprueba x cociente de probabilidad = odds postprueba) o un nomograma de Fagan (podéis repasar estos conceptos en la entrada correspondiente).
Por último, una tercera posibilidad es recurrir a otro de los inventos que se derivan del trabajo de Turing: la odds ratio diagnóstica (ORD).
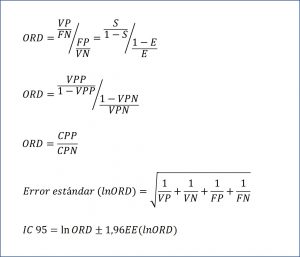
Por otra parte, la odds de que el sano dé positivo frente a que dé negativo es el cociente entre falsos positivos (FP) y verdaderos negativos (VN): FP/VN. Y visto esto, solo nos queda definir la razón entre las dos odds, tal como veis en la figura adjunta. La ORD puede también expresarse en función de los valores predictivos y de los cocientes de probabilidad, según las expresiones que podéis ver en la misma figura. Por último, decir que también es posible calcular su intervalo de confianza, según la fórmula que da fin a la figura.
Como toda odds ratio, los valores posibles de la ORD van de cero a infinito. El valor nulo es el uno, que significa que la prueba no tiene capacidad discriminatoria entre sanos y enfermos. Un valor mayor de uno indica capacidad discriminatoria, que será mayor cuanto mayor sea el valor. Por último, valores entre cero y uno nos indicarán que la prueba no solo no discrimina bien entre enfermos y sanos, sino que los clasifica de forma errónea y nos da más valores negativos entre los enfermos que entre los sanos.
La ORD es un medidor global fácil de interpretar y que no depende de la prevalencia de la enfermedad, aunque hay que decir que sí puede variar entre grupos de enfermos con distinta gravedad. Además, es también una medida muy robusta frente al efecto umbral y resulta muy útil para calcular las curvas ROC resumen que en seguida comentaremos.
El segundo aspecto peculiar del MAD que vamos a tratar es el efecto umbral. Siempre debemos valorar su presencia cuando nos encontremos ante un MAD. Lo primero será observar la heterogeneidad clínica entre los estudios primarios, que puede ser evidente sin necesidad de hacer muchas consideraciones. Existe también una forma matemática sencilla, que es calcular el coeficiente de correlación de Spearman entre sensibilidad y especificidad. Si existe efecto umbral existirá una correlación inversa entre ambas, tanto más fuerte cuanto mayor sea el efecto umbral.
Por último, un método gráfico es valorar la dispersión de la representación de sensibilidad y especificidad de los estudios primarios sobre la curva ROC resumen del metanálisis. Una dispersión nos permite sospechar el efecto umbral, pero también puede producirse por heterogeneidad de los estudios y por otros sesgos como el de selección o el de verificación.
El tercer elemento específico del MAD que vamos a comentar es el de la curva ROC resumen (ROCr), que es una estimación de la curva ROC común ajustada según los resultados de los estudios primarios de la revisión. Existen varias formas de calcularla, algunas bastante complicadas desde el punto de vista matemático, pero lo más utilizado son los modelos de regresión que emplean la ORD como estimador, ya que, como hemos dicho, es muy robusta frente a la heterogeneidad y al efecto umbral. Pero no os asustéis, la mayoría de los paquetes estadísticos calculan y representan las ROCr sin apenas esfuerzo.
La lectura de la ROCr es similar a la de cualquier curva ROC. Los dos parámetros que más se emplean son el área bajo la curva ROC (ABC) y el índice Q. El ABC de una curva perfecta será igual a 1. Valores por encima de 0,5 indicarán la capacidad discriminatoria de la curva diagnóstica, que será mayor cuanto más se aproxime a 1. Un valor de 0,5 nos dice que nos da igual hacer la prueba que elegir el resultado lanzando una moneda al aire. Finalmente, valores por debajo de 0,5 nos indican que la prueba no contribuye para nada al diagnóstico que pretende realizar.
Por su parte, el índice Q corresponde al punto en el que se igualan sensibilidad y especificidad. De manera similar al ABC, un valor superior a 0,5 indicará la eficacia global de la prueba diagnóstica, que será mayor cuánto más se aproxime a 1 el valor del índice Q. Además, pueden calcularse también los intervalos de confianza tanto del ABC como del índice Q, con lo que se podrá valorar la precisión de la estimación de la medida resumen del MAD.
Lectura crítica del metanálisis de pruebas diagnósticas
Una vez vistos (muy por encima) los aspectos específicos del MAD, vamos a dar unas recomendaciones para realizar la lectura crítica de este tipo de trabajos. La red CASPe no proporciona una herramienta específica para el MAD, pero podemos seguir las líneas de la revisión sistemática de estudios de tratamiento teniendo en cuenta los aspectos diferenciales del MAD. Como siempre, seguiremos nuestros tres pilares básicos: validez, importancia y aplicabilidad.
Empecemos con las preguntas que valoran la VALIDEZ del estudio.
La primera pregunta de eliminación hace referencia a si se ha planteado claramente el tema de la revisión. Al igual que cualquier revisión sistemática, la de pruebas diagnósticas debe tratar de responder a una pregunta concreta que sea relevante desde el punto de vista clínico, y que habitualmente se plantea siguiendo el esquema PICO de una pregunta clínica estructurada.
La segunda pregunta nos hace reflexionar si el tipo de estudios que se han incluido en la revisión son los adecuados. El diseño ideal es el de una cohorte a la que se aplica de manera ciega e independiente tanto la prueba diagnóstica que queremos valorar como el patrón de referencia. Otros estudios basados en diseños tipo caso-control son menos válidos para la evaluación de pruebas diagnósticas, por lo que disminuirán la validez de los resultados.
Si la respuesta a las dos preguntas anteriores es afirmativa, pasaremos a considerar los criterios secundarios. ¿Se han incluido los estudios importantes que tienen que ver con el tema? Debemos comprobar que se ha realizado una búsqueda global y no sesgada de la literatura. La metodología de la búsqueda es similar a la de las revisiones sistemáticas sobre tratamiento, aunque debemos tener algunas precauciones.
Por ejemplo, los estudios sobre diagnóstico suelen estar indexados de forma diversa en las bases de datos, por lo que el uso de los filtros habituales de otros tipos de revisiones puede hacer que perdamos trabajos relevantes. Tendremos que comprobar cuidadosamente la estrategia de búsqueda, que debe ser proporcionada por los autores de la revisión.
Además, debemos comprobar que los autores han descartado la posibilidad de un sesgo de publicación. Esto plantea un problema especial en los MAD, ya que el estudio del sesgo de publicación en estos estudios no está bien desarrollado y los métodos habituales como el funnel plot o el test de Egger no son muy fiables. Lo más prudente será suponer siempre que puede existir un sesgo de publicación.
Es muy importante que se haya hecho lo suficiente para valorar la calidad de los estudios, buscando la existencia de posibles sesgos. Para esto los autores pueden servirse de herramientas específicas, tales como la proporcionada por la declaración QUADAS-2.
Para finalizar el apartado de validez interna o metodológica, debemos preguntarnos si era razonable combinar los resultados de los estudios primarios. Es fundamental, para poder sacar conclusiones de datos combinados, que los trabajos sean homogéneos y que las diferencias entre ellos sean debidas únicamente al azar. Tendremos que valorar las posibles fuentes de heterogeneidad y si puede existir un efecto umbral, que los autores han debido tener en cuenta.
Resumiendo, los aspectos fundamentales que tendremos que analizar para valorar la validez de un MAD serán: 1) que los objetivos estén bien definidos; 2) que la búsqueda bibliográfica haya sido exhaustiva; y 3) que se haya comprobado también la validez interna o metodológica de los estudios incluidos. Además, revisaremos los aspectos metodológicos referentes a la técnica del metanálisis: conveniencia de combinar los estudios para realizar una síntesis cuantitativa, evaluación adecuada de la heterogeneidad de los estudios primarios y del posible efecto umbral y utilización de un modelo matemático adecuado para combinar los resultados de los estudios primarios (ROCr, ORD, etc.).
En cuanto a la IMPORTANCIA de los resultados debemos considerar cuál es el resultado global de la revisión y si la interpretación se ha hecho de forma juiciosa. Valoraremos más aquellos MAD que proporcionen medidas más robustas frente a los posibles sesgos, como los cocientes de probabilidades y la ORD. Además, hay que valorar la precisión de los resultados, para lo que recurriremos a nuestros queridos intervalos de confianza, que nos darán una idea de la precisión de la estimación de la verdadera magnitud del efecto en la población.
Concluiremos la lectura crítica del MAD valorando la APLICABILIDAD de los resultados a nuestro medio. Habrá que preguntarse si podemos aplicar los resultados a nuestros pacientes y cómo van a influir en la atención que les prestemos. Tendremos que fijarnos si los estudios primarios de la revisión describen a los participantes y si se parecen a nuestros pacientes. Además, habrá que ver si se han considerado todos los resultados relevantes para la toma de decisiones en el problema en estudio y, como siempre, habrá que valorar la relación beneficios-costes-riesgos. El que la conclusión de la revisión nos parezca válida no quiere decir que tengamos que aplicarla de forma obligada.
Nos vamos…
Pues con todo lo dicho vamos a ir terminando por hoy. El título de esta entrada hace referencia al maltrato sufrido por un genio. Ya sabemos a qué genio nos referíamos: Alan Turing. Aclararemos lo del maltrato. A pesar de ser una de las mentes más brillantes del siglo XX, como lo atestiguan sus trabajos sobre estadística, computación, criptografía, cibernética, etc., y de haber salvado a su país del bloqueo de la Armada alemana durante la guerra, en 1952 fue juzgado por su homosexualidad y condenado por indecencia grave y perversión sexual.
Como es fácil comprender, su carrera terminó tras el juicio y Alan Turing falleció en 1954, aparentemente tras comerse un trozo de una manzana envenenada con cianuro, lo que se etiquetó como un suicidio, aunque hay teorías que hablan más bien de asesinato. Dicen que de aquí viene la manzana mordida de una conocida marca de ordenadores, aunque hay otros que dicen que la manzana representa sin más un juego de palabras entre bite (mordida, en inglés) y byte (término informático).
No sé cuál de las dos teorías será cierta, pero yo prefiero acordarme de Turing cada vez que veo la manzanita. Un humilde tributo a un gran hombre.
Y ahora ya sí que acabamos. Hemos visto muy por encima las peculiaridades de los metanálisis de pruebas diagnósticas y cómo valorarlos. Podría decirse mucho más de toda la matemática asociada a sus aspectos específicos como la presentación de variables, el estudio del sesgo de publicación, del efecto umbral, etc. Pero esa es otra historia…
