El significado del valor de p.

Se explica el significado del valor de p: la probabilidad de obtener un valor igual o más distante de la igualdad de efecto si la hipótesis nula es cierta.

La estadística se nos atraganta un poco a la mayoría de los que nos denominamos “clínicos”. Los conocimientos sobre el tema adquiridos durante nuestros años de formación hace tiempo que habitan en el mundo neblinoso del olvido. Recordamos vagamente términos como distribución de probabilidad, contraste de hipótesis, análisis de la varianza, regresión… Es por este motivo que siempre nos da un poco de aprensión cuando llegamos al apartado de métodos de los artículos científicos, en los que se detallan todas estas técnicas que, aunque nos resultan conocidas, no conocemos con la profundidad suficiente para interpretar correctamente sus resultados.

Menos mal que la Providencia nos ha puesto un salvavidas: nuestra querida e idolatrada p. ¿Quién no se habrá perdido con una descripción farragosa de métodos matemáticos para respirar, por fin, aliviado al encontrar el valor de p? Sobre todo, si la p es pequeña y tiene muchos ceros.

El problema con la p es que, aunque es unánimemente idolatrada, también es mayoritariamente incomprendida. Su valor es, con mucha frecuencia, malinterpretado. Y esto es así porque muchos albergamos ideas erróneas sobre lo que significa realmente el valor de p.

Vamos a intentar aclararlo.

El significado del valor de p

Siempre que queremos saber algo sobre una variable, el efecto de una exposición, la comparación de dos tratamientos, etc., nos encontraremos con la ubicuidad del azar: está en todas partes y nunca podemos librarnos de él, aunque podemos intentar limitarlo y, desde luego, tratar de medir su efecto.

Pongamos un ejemplo para entenderlo mejor. Supongamos que hacemos un ensayo clínico para comparar el efecto de dos dietas, A y B, sobre la ganancia de peso en dos grupos de participantes. Simplificando, el resultado del ensayo tendrá una de las tres características: los de la dieta A ganan más peso, los de la dieta B ganan más peso, ambos grupos ganan igual peso (podría haber, incluso, una cuarta: los dos grupos pierden peso). En cualquier caso, siempre vamos a obtener un resultado diferente, aunque sea por azar (incluso en el supuesto de que las dos dietas sean iguales).

Imaginaos que los de la dieta A engordan 2 kg y los de la dieta B, 3 kg. ¿Se engorda más con la dieta B o la diferencia se debe al azar (muestras elegidas, variabilidad biológica, imprecisión de mediciones, etc.)? Aquí es donde entra nuestro contraste de hipótesis.

Cuando nosotros vamos a hacer el ensayo partimos de la hipótesis de igualdad, de no diferencia de efecto (se engorda igual con las dos dietas). Esto es lo que llamamos hipótesis nula (H0) que, repito para que quede claro, asumimos que es la cierta. Si la variable que estamos midiendo sigue una distribución de probabilidad conocida (normal, ji-cuadrado, t de Student, etc.), podemos calcular la probabilidad de presentarse cada uno de los valores de la distribución. En otras palabras, podemos calcular la probabilidad de obtener un resultado tan distinto de la igualdad como el que hemos obtenido, siempre bajo el supuesto de la H0.

Ese es el valor de p: la probabilidad de que la diferencia de resultado observada se deba al azar. Por convenio, si esa probabilidad es menor del 5% (0,05) nos parecerá poco probable que la diferencia se deba al azar y rechazaremos H0, la hipótesis de igualdad, aceptando la hipótesis alternativa (Ha) que, en este ejemplo, dirá que una dieta engorda más que la otra. Por otra parte, si la probabilidad es mayor del 5%, no nos sentiremos lo suficientemente seguros para afirmar que la diferencia no se debe a la casualidad, así que NO rechazamos H0 y nos quedamos con la hipótesis de igualdad: las dos dietas son similares.

Tened en cuenta que siempre nos movemos en el terreno de la probabilidad. Si la p es menor de 0,05 (estadísticamente significativa), rechazaremos H0, pero siempre con una probabilidad de cometer un error de tipo 1: dar por bueno un efecto que, en realidad, no existe (un falso positivo). Por otra parte, si p es mayor de 0,05, nos quedamos con H0 y decimos que no hay diferencia de efecto, pero siempre con una probabilidad de cometer un error de tipo 2: no detectar un efecto que, en realidad, existe (falso negativo).

¿Qué no es p?

Podemos ver, por tanto, que el valor de p es algo sencillo desde el punto de vista conceptual. Sin embargo, hay una serie de errores habituales sobre lo que representa o no representa el valor de p. Vamos a tratar de aclararlos.

Es falso que una p menor de 0,05 signifique que la hipótesis nula es falsa y una p mayor de 0,05 que la hipótesis nula es cierta. Como ya hemos mencionado, el abordaje es siempre probabilístico. La p < 0,05 solo quiere decir que, por convenio, es poco probable que H0 sea cierta, así que la rechazamos, aunque siempre con una pequeña probabilidad de equivocarnos. Por otra parte, si p > 0,05 tampoco se asegura que H0 sea cierta, ya que puede existir un efecto real y que el estudio no tenga potencia suficiente para detectarlo.

En este punto hay que recalcar un hecho: la hipótesis nula solo es falsable. Esto quiere decir que solo podemos rechazarla (con lo que nos quedamos con Ha, con una probabilidad de error), pero nunca podemos afirmar que es cierta. Si p > 0,05 no podremos rechazarla, así que nos mantendremos en el supuesto inicial de igualdad de efecto, que no podemos demostrar de una forma positiva.

Es falso que el valor de p tenga relación con la fiabilidad del estudio. Podemos pensar que las conclusiones del estudio serán más fiables cuanto menor sea el valor de p, pero tampoco es cierto. En realidad, el valor de p es la probabilidad de obtener un valor semejante por azar si repetimos el experimento en las mismas condiciones y no solo depende de que el efecto que queremos demostrar exista o no. Hay otros factores que pueden influir en la magnitud de la p: el tamaño de la muestra, el tamaño del efecto, la varianza de la variable medida, la distribución de probabilidad empleada, etc.

Es falso que el valor de p indique la importancia del resultado. Como ya hemos repetido varias veces, el valor de p solo es la probabilidad de que la diferencia observada se deba al azar. Una diferencia estadísticamente significativa no tiene obligatoriamente que ser clínicamente importante. La importancia clínica la establece el investigador y es posible encontrar resultados con una p muy pequeña que no sean importantes desde el punto de vista clínico y viceversa, valores no significativos que sean importantes.

Es falso que el valor de p represente la probabilidad de que la hipótesis nula sea cierta. Esta creencia hace que, a veces, busquemos el valor exacto de p y no nos conformemos con saber solo si es mayor o menor de 0,05. La culpa de este error de concepto la tiene una mala interpretación de la probabilidad condicional. A nosotros nos interesa saber cuál es la probabilidad de que H0 sea cierta una vez que hemos obtenido unos resultados con nuestro ensayo. Expresado matemáticamente, queremos saber P(H0|resultados). Sin embargo, el valor de p lo que nos proporciona es la probabilidad de obtener nuestros resultados bajo el supuesto de que la hipótesis nula es cierta, o sea, P(resultados|H0).

Por tanto, si interpretamos que la probabilidad de que H0 sea cierta a la vista de nuestros resultados (P(H0|resultados)) es igual al valor de p (P(resultados|H0)) estaremos cayendo en una falacia inversa o falacia de la transposición de los condicionales.

En realidad, la probabilidad de que H0 sea cierta no depende solo de los resultados del estudio, sino que también se ve influida por la probabilidad previa que se estimase antes del estudio, que es una medida de la creencia subjetiva que refleja su plausibilidad, generalmente basada en estudios y conocimientos previos. Pensemos que queremos contrastar un efecto que creemos muy poco probable que sea cierto. Valoraremos con precaución un valor de p < 0,05, aunque sea significativo. Por el contrario, si estamos convencidos de que el efecto existe, con poca p nos daremos por satisfechos.

En resumen, para calcular la probabilidad de que el efecto sea real deberemos calibrar el valor de p con el valor de la probabilidad basal de H0, que será asignada por el investigador o por datos previos disponibles. Existen métodos matemáticos para calcular esta probabilidad en función de su probabilidad basal y el valor de p, pero lo más sencillo es recurrir a una herramienta gráfica que es el nomograma de Held, que podéis ver en la figura.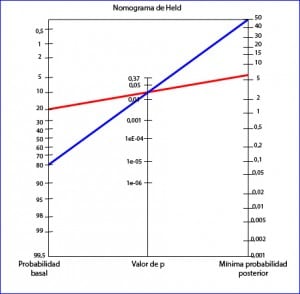

Para utilizar el nomograma de Held solo tenemos que trazar una línea desde la probabilidad previa que consideremos que tiene H0 hasta el valor de p y prolongarla para ver qué valor de probabilidad posterior alcanzamos. Como ejemplo, hemos representado un estudio con un valor de p = 0,03 en el que creemos que la probabilidad de la H0 es del 20% (creemos que hay un 80% de que el efecto sea real).

Si prolongamos la línea nos dice que la probabilidad mínima de H0 del 6%: hay un 94% de probabilidad de que el efecto sea real. Por otro lado, pensad en otro estudio con el mismo valor de p pero en el que pensamos que la probabilidad del efecto es más baja, por ejemplo, del 20% (la probabilidad de H0 es del 80%), Para un mismo valor de p, la probabilidad mínima posterior de H0 es del 50%, luego hay un 50% de que el efecto sea real. Vemos, así, como la probabilidad posterior cambia según la probabilidad previa.

Nos vamos…

Y hasta aquí hemos llegado por hoy. Hemos visto cómo la p solo nos da una idea del papel que el azar ha podido tener en nuestros resultados y que, además, puede depender de otros factores, quizás el más importante el tamaño muestral. La conclusión es que, en muchas ocasiones, el valor de p es un parámetro que permite valorar de forma muy limitada la importancia de los resultados de un estudio. Para hacerlo mejor, es preferible recurrir al uso de los intervalos de confianza, que nos permitirán valorar la importancia clínica y la significación estadística. Pero esa es otra historia…