El método de los mínimos cuadrados.

El otro día estaba intentando medir la distancia entre Madrid y Nueva York en Google Earth y me encontré con algo inesperado: cuando intentaba trazar una línea recta entre las dos ciudades, esta se torcía y formaba un arco, y no había forma de evitarlo.

Me quedé pensando si no sería verdad aquello que dijo Euclides de que la línea recta es el camino más corto entre dos puntos. Claro que, en seguida, me di cuenta de dónde estaba el error: Euclides pensaba en la distancia entre dos puntos situados en un plano y yo estaba dibujando la distancia mínima entre dos puntos situados en una esfera. Evidentemente, en este caso la distancia más corta no la marca una recta, sino un arco, tal como Google me mostraba.

Y como una cosa lleva a la otra, esto me llevó a pensar en qué pasaría si en vez de dos puntos hubiese muchos más. Esto tiene que ver, como algunos ya imagináis, con la recta de regresión que se calcula para ajustarse a una nube de puntos.

Aquí, como es fácil comprender, la recta no puede pasar por todos los puntos sin perder su rectitud, así que los estadísticos idearon una forma para calcular la recta que más se aproxime en promedio a todos los puntos. El método que más utilizan es el que llaman método de los mínimos cuadrados, cuyo nombre hace presagiar algo extraño y esotérico. Sin embargo, el razonamiento para calcularlo es mucho más sencillo y, por ello, no menos ingenioso. Veámoslo.

El método de los mínimos cuadrados

El modelo de regresión lineal posibilita, una vez establecida una relación lineal, efectuar predicciones sobre el valor de una variable Y sabiendo los valores de un conjunto de variables X₁, X₂,… X_n. A la variable Y la llamamos dependiente, aunque también se la conoce como variable objetivo, endógena, criterio o explicada. Por su parte, las variables X son las variables independientes, conocidas también como predictoras, explicativas, exógenas o regresoras.

Cuando hay varias variables independientes nos encontramos ante un modelo de regresión lineal múltiple, mientras que cuando hay solo una hablaremos de la regresión lineal simple. Por hacerlo más sencillo, nos centraremos, cómo no, en la regresión simple, aunque el razonamiento vale también para la múltiple.

Como ya hemos dicho, la regresión lineal requiere eso, que la relación entre las dos variables sea lineal, así que puede representarse mediante la siguiente ecuación de una línea recta:

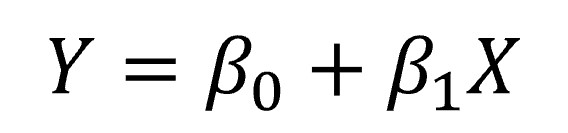
Aquí nos encontramos con dos amigos nuevos acompañando a nuestras variables dependiente e independiente: son los coeficientes del modelo de regresión. β₀ representa la constante del modelo (también llamada intercepto) y es el punto donde la recta corta el eje de ordenadas (el de las Y, para entendernos bien). Representaría el valor teórico de la variable Y cuando la variable X vale cero.

Por su parte, β₁ representa la pendiente (inclinación) de la recta de regresión. Este coeficiente nos dice el incremento de unidades de la variable Y que se produce por cada incremento de una unidad de la variable X.

Nos volvemos a encontrar con el azar

Esta sería la recta teórica general del modelo. El problema es que la distribución de valores no se va a ajustar nunca de manera perfecta a ninguna recta así que, cuando vayamos a calcular un valor de Y determinado (y_i) a partir de un valor de X (x_i) habrá una diferencia entre el valor real de y_i y el que obtengamos con la fórmula de la recta. Ya nos hemos vuelto a encontrar con el azar, nuestro compañero inseparable, así que no tendremos más remedio que incluirlo en la ecuación:

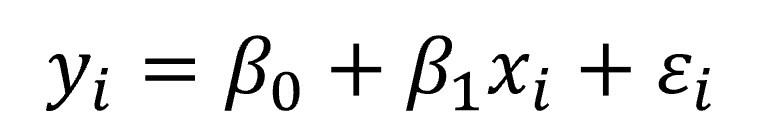
Aunque parezca una fórmula similar a la anterior, ha sufrido una profunda transformación. Ahora tiene dos componentes bien diferenciados, un componente determinista y otro estocástico (error). El componente determinista lo marcan los dos primeros elementos de la ecuación, mientras que el estocástico lo marca el error en la estimación. Los dos componentes se caracterizan por su variable aleatoria, y_i y ε_i, respectivamente, mientras que x_i sería un valor determinado y conocido de la variable X.

Vamos a centrarnos un poco en el valor de ε_i. Ya hemos dicho que representa la diferencia entre el valor real de y_i en nuestra nube de puntos y el que nos proporcionaría la ecuación de la recta (el valor estimado, representado como ŷ_i). Podemos representarlo matemáticamente de la siguiente forma:

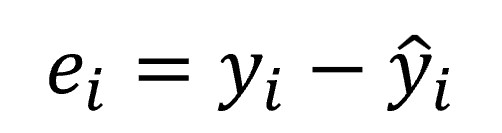
Este valor se conoce con el nombre de residuo y su valor depende del azar, aunque si el modelo no está bien especificado pueden también influir otros factores de manera sistemática, pero eso no nos influye para lo que estamos tratando.

Recapitulemos

Vamos a recapitular lo que tenemos hasta aquí:

1. Una nube de puntos sobre la que queremos dibujar la recta que mejor se ajuste a la nube.
2. Un número infinito de rectas posibles, de entre las que queremos seleccionar una concreta.
3. Un modelo general con dos componentes: uno determinista y otro estocástico. Este segundo va a depender, si el modelo es correcto, del azar.

Los valores de las variables X e Y ya los tenemos en nuestra nube de puntos para la que queremos calcular la recta. Lo que variará en la ecuación de la recta que seleccionemos serán los coeficientes del modelo, β_{0 y} β₁. ¿Y qué coeficientes nos interesan? Lógicamente, aquellos con los que el componente aleatorio de la ecuación (el error) sea lo menor posible. Dicho de otra forma, queremos la ecuación con un valor de la suma de residuos lo más bajo posible.

Partiendo de la ecuación anterior de cada residuo, podemos representar la suma de residuos de la forma siguiente, donde n es el número de pares de valores de X e Y de que disponemos:

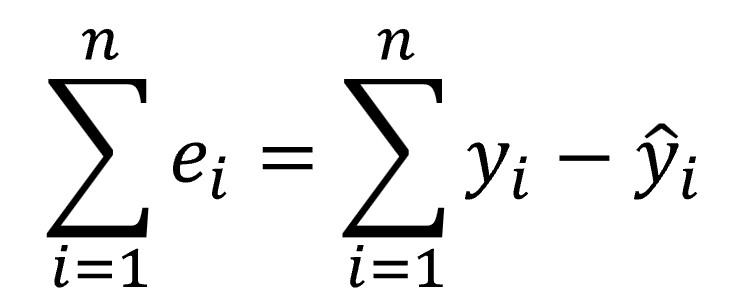
Pero esta fórmula no nos sirve. Si la diferencia entre el valor estimado y el real es aleatoria, unas veces será positiva y otras, negativa. Es más, su media será o estará muy próxima a cero. Por este motivo, como en otras ocasiones en las que lo que interesa es medir la magnitud de la desviación, tenemos que recurrir a un método que impida que los negativos se anulen con los positivos, así que calculamos estas diferencias elevadas al cuadrado, según la fórmula siguiente:

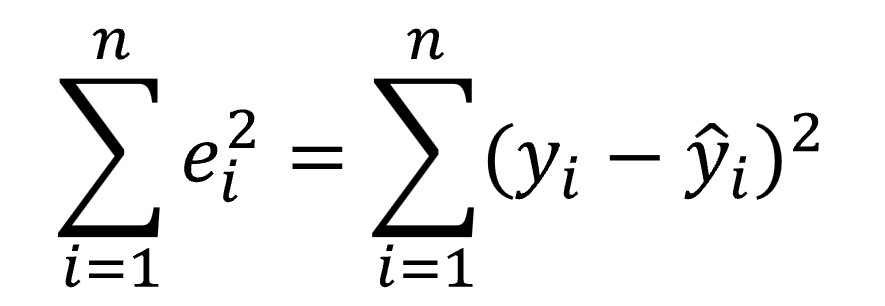
¡Ya lo tenemos!

¡Por fin! Ya sabemos de dónde viene el método de los mínimos cuadrados: buscamos la recta de regresión que nos proporcione un valor lo menor posible de la suma de los cuadrados de los residuos. Para calcular los coeficientes de la recta de regresión solo tendremos que ampliar un poco la ecuación anterior, sustituyendo el valor estimado de Y por los términos de la ecuación de la recta de regresión:

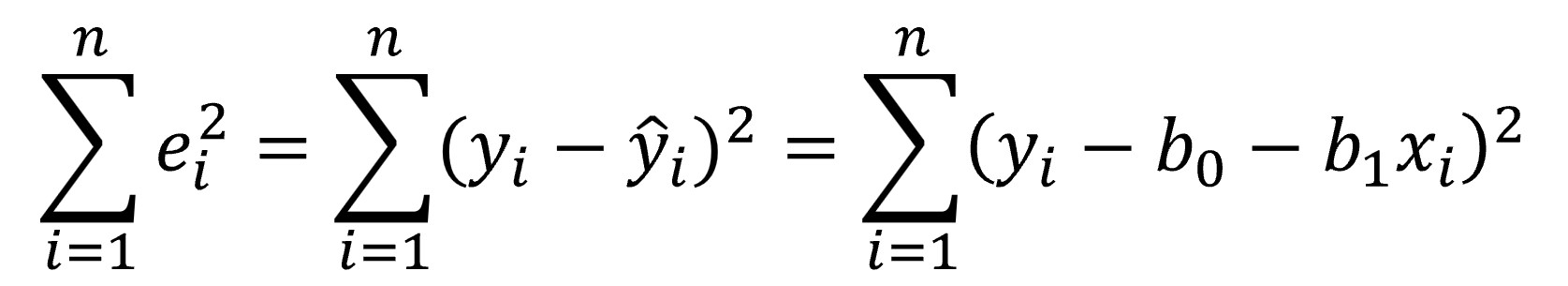
y encontrar los valores de b₀ y b₁ que minimicen la función. A partir de aquí la cosa es coser y cantar, solo tenemos que igualar a cero las derivadas parciales de la ecuación anterior (tranquilos, vamos a ahorrarnos la jerga matemática dura) para obtener el valor de b₁:

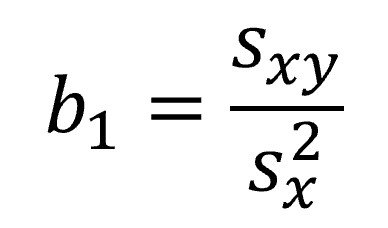
Donde tenemos en el numerador la covarianza de las dos variables y, en el denominador, la varianza de la variable independiente. A partir de aquí, el cálculo de b₀ es pan comido:

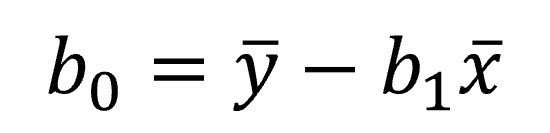
Ya podemos construir nuestra recta que, si os fijáis un poco, pasa por los valores medios de X e Y.

Un ejemplo práctico

Y con esto terminamos la parte ardua de esta entrada. Todo lo que hemos dicho es para poder comprender qué significa lo de los mínimos cuadrados y de dónde viene el asunto, pero no es necesario hacer todo esto para calcular la recta de regresión lineal. Los paquetes estadísticos lo hacen en un abrir y cerra de ojos.

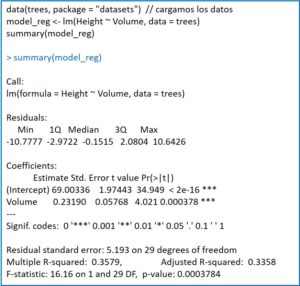
Por ejemplo, en R se calcula mediante la función lm(), iniciales de linear model. Veamos un ejemplo utilizando la base de datos “trees” (circunferencia, volumen y altura de 31 observaciones sobre árboles), calculando la recta de regresión para estimar el volumen de los árboles conociendo su altura:

modelo_reg <- lm(Height~Volume, data = trees)

summary(modelo_reg)

La función lm() devuelve el modelo a la variable que le hemos indicado (modelo_reg, en este caso), que podremos explotar después, por ejemplo, con la función summary(). Esto nos proporcionará una serie de datos, tal como podéis ver en la figura adjunta.

En primer lugar, los cuartiles y la mediana de los residuos. Para que el modelo sea correcto interesa que la mediana esté próxima a cero y que los valores absolutos de los residuos se distribuyan de manera uniforme entre los cuartiles (similar entre máximo y mínimo y entre primer y tercer cuartil).

A continuación, se muestra la estimación puntual de los coeficientes junto con su error estándar, lo que nos permitirá calcular sus intervalos de confianza. Esto se acompaña de los valores del estadístico t con su significación estadística. No lo hemos dicho, pero los coeficientes siguen una distribución de la t de Student con n-2 grados de libertad, lo que nos permite saber si son estadísticamente significativos.

Por último, se proporciona la desviación estándar de los residuos, el cuadrado del coeficiente de correlación múltiple o coeficiente de determinación (la precisión con que la recta representa la relación funcional entre las dos variables; su raíz cuadrada en regresión simple es el coeficiente de correlación de Pearson), su valor ajustado (que será más fiable cuando calculemos modelos de regresión con muestras pequeñas) y el contraste F para validar el modelo (los cocientes de las varianzas siguen una distribución de la F de Snedecor).

Así, nuestra recta de regresión quedaría de la siguiente manera:

Altura = 69 + 0,23xVolumen

Ya podríamos calcular qué altura tendría un árbol con un volumen determinado que no estuviese en nuestra muestra (aunque debería estar dentro del rango de datos utilizados para calcular la recta de regresión, ya que es arriesgado hacer predicciones fuera de este intervalo).

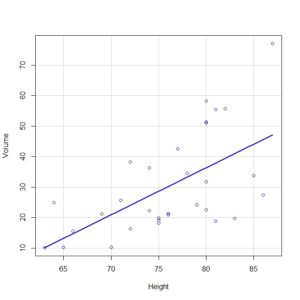
Además, con el comando scatterplot(Volume ~ Height, regLine = TRUE, smooth = FALSE, boxplots = FALSE, data = trees), podríamos dibujar la nube de puntos y la recta de regresión, como podéis ver en la segunda figura.

Y podríamos calcular muchos más parámetros relacionados con el modelo de regresión calculado por R, pero lo vamos a dejar aquí por hoy.

Nos vamos…

Antes de terminar, deciros que el método de los mínimos cuadrados no es el único que nos permite calcular la recta de regresión que mejor se ajuste a nuestra nube de puntos. Existe también otro método que es el de la máxima verosimilitud, que da más importancia a la elección de los coeficientes más compatibles con los valores observados. Pero esa es otra historia…