Cribado.
Se describen las características del cribado diagnóstico y las formas de calcular la prevalencia de la enfermedad a partir de sus resultados.
Nadie es perfecto. Es un hecho. Y un consuelo también. Porque el problema no es ser imperfecto, que es algo inevitable. El verdadero problema estriba en creerse perfecto, en ser ignorante de las propias limitaciones. Y lo mismo ocurre con otras muchas cosas, como las pruebas diagnósticas que utilizamos en medicina.
Aunque lo de las pruebas diagnósticas tiene mucho más delito porque, más allá de su imperfección, se permiten tratar de forma diferente a sanos y enfermos. ¿No me creéis?. Vamos a hacer unas reflexiones.
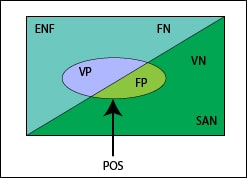
Para empezar, echad un vistazo al diagrama de Venn que os he dibujado. ¡Qué recuerdos de infancia me traen estos diagramas!. El cuadrado simboliza nuestra población en cuestión. De la diagonal para arriba están los enfermos (ENF) y de la diagonal para abajo los sanos (SAN), con lo que cada área representa la probabilidad de estar SAN o ENF.
El área del cuadrado, obviamente, vale 1: es seguro que uno está o enfermo o sano, situaciones mutuamente excluyentes. La elipse engloba a los sujetos a los que realizamos la prueba diagnóstica y obtenemos un resultado positivo (POS). En un mundo perfecto, toda la elipse estaría por encima de la diagonal, pero en el mundo imperfecto real la elipse está cruzada por la diagonal, con lo que los resultados POS pueden ser verdaderos (VP) o falsos (FP), estos últimos cuando se obtienen en sanos. La superficie fuera de la elipse serían los resultados negativos (NEG) que, como podéis ver, también se dividen en verdaderos y falsos (VN, FN).
Rendimiento del cribado
Ahora traslademos esto a la típica tabla de contingencia que definiría las probabilidades de las diferentes opciones y pensemos en una situación en la que todavía no hemos realizado la prueba. En este caso, las columnas condicionan las probabilidades de los sucesos de las filas. Por ejemplo, la casilla superior izquierda representa la probabilidad de obtener POS en los ENF (una vez que uno está enfermo, ¿qué probabilidad hay de obtener un resultado positivo?), lo que denominamos sensibilidad (SEN).
Por su parte, la inferior derecha representa la probabilidad de obtener un NEG en un SAN, lo que llamamos especificidad(ESP). El total de la primera columna representa la probabilidad de estar enfermo, que no es más que la prevalencia(PRV) y, así, podemos discernir qué significado tiene la probabilidad de cada celda. Esta tabla nos proporciona dos características de la prueba, SEN y ESP, que, como sabemos, son intrínsecas a la prueba siempre que se realice en unas condiciones similares, aunque las poblaciones sean diferentes.
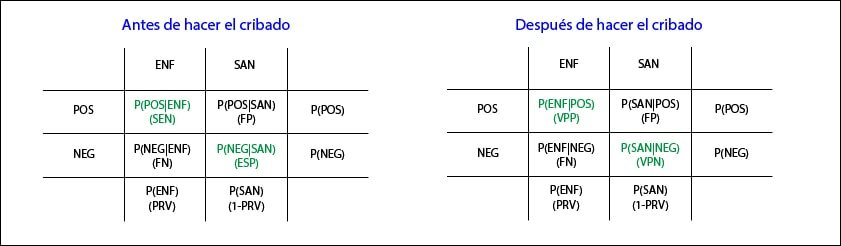
¿Y qué pasa con la tabla de contingencia una vez que hemos realizado la prueba?. Se produce un cambio sutil, pero muy importante: ahora son las filas las que condicionan las probabilidades de los sucesos de las columnas.
Los totales de la tabla no cambian pero fijaos que, ahora, la primera celda representa la probabilidad de estar ENF una vez que se ha dado POS (cuando da positivo, ¿qué probabilidad hay de que realmente esté enfermo?) y esto ya no es la SEN, sino el valor predictivo positivo (VPP). Lo mismo ocurre con la celda inferior derecha, que ahora representa la probabilidad de estar SAN una vez que se obtiene un NEG: valor predictivo negativo (VPN).
Vemos, pues, que antes de realizar la prueba conoceremos habitualmente su SEN y ESP, mientras que una vez realizada, lo que obtendremos será sus valores predictivos positivo y negativo, quedando estas cuatro características de la prueba ligadas para siempre entre sí gracias a la magia del teorema de Bayes. Claro que, en el caso del VPP y VPN hay un quinto en discordia: la prevalencia. Ya sabemos que los valores predictivos varían en función de la PRV de la enfermedad en la población, aunque se mantengan sin cambios la SEN y ESP de la prueba.
Un ejemplo de cribado
Y todo esto tiene su traducción práctica. Vamos a inventarnos un ejemplo para liarlo todo un poco más. 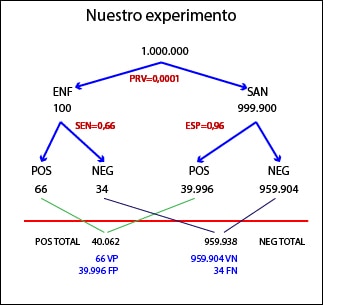
Sabiendo la PREV es fácil calcular que en nuestra población hay 100 ENF. De éstos, 66 darán POS (SEN=0,66) y 34 darán NEG. Por otra parte, habrá 990.900 sanos, de los que el 96% (959.904) darán NEG (ESP=0,96) y el resto (39.996) darán POS. En resumen, que obtendremos 40.062 POS, de los cuales 39.996 serán FP.
Que nadie se asuste del alto número de falsos positivos. Esto es debido a que hemos elegido una enfermedad muy rara, por lo que hay muchos FP a pesar de que la ESP sea bastante alta. Pensad que, en la vida real, habría que hacer pruebas de confirmación a todos estos sujetos para acabar confirmando el diagnóstico solo en 66 personas. Por eso es tan importante pensar bien si merece la pena hacer un cribado antes de ponerse a buscar enfermedades en la población. Por eso, y por otras razones.
Ya podemos calcular los valores predictivos. El VPP será el cociente entre POS verdaderos y el total de POS: 66/40.062 = 0,0016. O sea, que habrá un enfermo por cada 1.500 positivos, más o menos. De manera similar, el VPN será el cociente entre NEG verdaderos y NEG totales: 959.904/959.938 = 0,99. Como era de esperar, dada la alta ESP de la prueba, un resultado negativo hace altamente improbable que uno esté enfermo.
¿Qué os parece?. ¿Es útil la prueba como herramienta de cribado poblacional con ese número de falsos positivos y un VPP de 0,0016?. Pues, aunque pueda parecer raro, si lo pensamos un momento, no es tan mala.
La probabilidad preprueba de estar ENF es 0,0001 (la PRV). La probabilidad postprueba es 0,0016 (el VPP). Luego su cociente tiene un valor de 0,0016/0,0001 = 16, lo que quiere decir que hemos multiplicado por 16 nuestra capacidad de detectar al enfermo. La prueba, pues, no parece tan mala, aunque habrá que tener en cuenta otros muchos factores antes de ponernos a cribar.
Cálculos con el cribado
Todo esto que hemos visto hasta ahora tiene una aplicación práctica adicional. Supongamos que solo conocemos SEN y ESP, pero desconocemos la PRV de la enfermedad en la población que hemos cribado. ¿Podemos estimarla a partir de los resultados de la prueba de cribado?. La respuesta es, claro está, que sí.
Imaginemos de nuevo nuestra población de un millón de sujetos. Les hacemos la prueba y obtenemos 40.062 positivos. El problema aquí radica en que parte de estos (la mayoría) son FP. Además, no sabemos cuántos enfermos han dado negativo (FN). ¿Cómo podemos conocer entonces el número de enfermos de la población?. Pensando un poco.
Ya hemos dicho que el número de enfermos será igual al número de positivos menos los FP más los FN:
Nº enfermos = POS totales – número de FP + número de FN
Los POS los tenemos: 40.062. Los FP serán aquéllos sanos (1-PRV) que den positivo siendo sanos (los sanos que no dan negativo: 1-ESP). Luego el número total de FP será:
FP = (1-PRV)(1-EPS) x n (1 millón, el tamaño de la población).
Por último, los FN serán los enfermos (PRV) que no den positivo (1-SEN). Luego el número total de FN será:
FN = PRV(1-SEN) x n (1 millón, el tamaño de nuestra población).
Si sustituimos los totales de FP y FN en la primera ecuación por los valores que acabamos de deducir, podremos despejar la PRV, obteniendo la fórmula siguiente:
Ya podemos calcular la prevalencia en nuestra población:
Nos vamos…
Bueno, creo que se me acaba de fundir un lóbulo, así que vamos a tener que dejarlo aquí. Una vez más hemos contemplado la magia y el poder de los números y hemos visto cómo podemos hacer trabajar a nuestro favor las imperfecciones de nuestras herramientas. Podríamos, incluso, ir un poco más allá y calcular la precisión de la estimación que hemos realizado. Pero esa es otra historia…
