Distribución de la t de Student.

A mí con la cerveza me pasa algo parecido a lo que me ocurre con el chocolate: me gustan todos los tipos, absolutamente todos, excepto los que llevan fruta, especialmente si son cerezas. Reconozco que la fruta es un alimento sano y recomendable, pero prefiero cada cosa en su sitio y no hacer mezclas raras.

Ya hablamos un día de chocolate, así que hoy hablaremos de cerveza. O, mejor dicho, de un personaje ilustre del mundo de la cerveza, que vivió a caballo entre los siglos XIX y XX, nada menos que de William Sealy Gosset.

¿Qué no sabéis quién era? Esperad un poco y veréis como sí.

Un poco de historia

Lo que seguro que todos conocéis es la cerveza Guinness, esa cerveza tostada, yo diría más bien negra, de sabor tan característico y con una espuma tan blanca y densa que ayudó a crear la leyenda, falsa por lo demás, de que llevaba café como parte de su composición.

William Sealy Gosset trabajaba en la Guinness a comienzos del pasado siglo XX y aplicaba sus conocimientos sobre estadística para controlar la calidad y mejorar tanto la malta que se cultivaba en la granja como la cerveza que se fabricaba en la destilería.

El problema que tenía Gosset es que trabajaba con muestras pequeñas, por lo que estaba sujeto a errores en sus estimaciones, sobre todo cuando tenía valores extremos en sus muestras.

Así que, ayudado por un amigo suyo, un tal Pearson, cuyo nombre espero que sí os dirá algo, elaboró una nueva distribución de probabilidad, la conocida distribución de la t de Student, de la que vamos a hablar hoy.

La distribución de la t de Student

Hoy en día, la distribución de la t de Student es una de las más utilizadas en la inferencia estadística asociada a muestras pequeñas, de forma que es la que se suele utilizar para el contraste de una media muestral con la poblacional y para la comparación de dos medias.

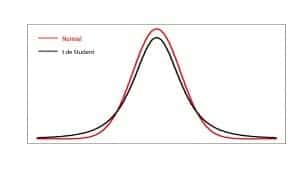
Se parece bastante a una distribución normal estándar, aunque, mientras la normal se define por su media y su varianza, la distribución de la t de Student incorpora, además, sus grados de libertad, por lo que se suele denominar como t_n, siendo n el número de grados de libertad, que habitualmente se calculan como n-1 (n es el tamaño de la muestra).

Su forma, como hemos dicho, es similar a la de la distribución normal, centrada en cero, acampanada y simétrica, aunque la t de Student presenta unas colas más pesadas que la curva de Gauss. Esto implica una mayor dispersión de los datos, lo que motiva que las estimaciones sean menos precisas y los intervalos de confianza sean más amplios que los que se obtendrían aplicando la distribución normal.

De todas formas, estas diferencias van desapareciendo según aumenta el tamaño de la muestra. Cuando n es grande, puede hacerse una aproximación con una normal con un grado de error mínimo. Esto es así porque las características de las colas dependen de los grados de libertad de la distribución, siendo más ligeras al aumentar el número de grados de libertad y, por tanto, el tamaño muestral.

En resumen, y para decirlo de una forma más técnica, a medida que disminuye el tamaño muestral (y los grados de libertad) aumenta la probabilidad acumulada en las colas, y viceversa. Una distribución de la t de Student con 30 o más grados de libertad es prácticamente indistinguible de una distribución normal con la misma media y varianza.

La utilidad de la distribución de la t de Student

Como ya hemos dicho, Pearson ayudó a Gosset a tabular la distribución y, para redondear la faena, se lo publicó en su revista, que se llamaba Biometrika. Pero Pearson, con todo lo listo que era, no se dio cuenta de la importancia del hallazgo de Gosset.

Menos mal que Gosset tenía muchos amigos (¿tendría algo que ver con trabajar en una destilería?) y otro de ellos sí que supo ver lo revolucionario del método. Se trata, nada más y nada menos, que del gran Ronald Fisher, del que ya hemos hablado también en alguna entrada anterior.

Efectivamente, fue Fisher el que introdujo el concepto de grados de libertad, que tanta importancia tienen para esta distribución, ya que permiten ajustar el efecto de la desviación de las estimaciones producido por el tamaño muestral pequeño, aunque, claro está, pagando el precio de obtener una menor precisión, sobre todo con las muestras más pequeñas.

Esto es lo que permite poder utilizar la distribución de la t de Student para estimar el valor de la media poblacional de una variable aleatoria que sigue una distribución normal cuando el parámetro se extrae de una muestra pequeña y se desconoce la varianza poblacional.

Además, como ya hemos mencionado, se utiliza en el contraste de hipótesis entre dos medias cuando la variable aleatoria sigue una distribución normal y existe igualdad de varianzas (homocedasticidad) entre los dos grupos que se contrastan.

Un poco más de historia antes de terminar

Llegados a este punto, los que no conozcáis la historia de las aventuras de Gosset estaréis preguntándoos por qué la llamamos t de Student y no t de Gosset.

Sobre este asunto, al igual que ocurría con la manzana mordida de Apple, hay dos versiones.

La versión más extendida afirma que la Guinness había prohibido a sus empleados publicar artículos de cualquier tipo. Esto se debía a que un empleado anterior había publicado secretos de la destilería, que quería, con esta prohibición, evitar la fuga de más información confidencial. Por eso Gosset publicó su trabajo en Biometrika firmando con el pseudónimo de Student.

Pero a mi me gusta más otra versión menos conocida, pero mucho más bonita. Una empresa moderna y progresista como Guinness entendía la necesidad de aplicar los conocimientos de estadística para mejorar su producción, pero no quería que la competencia hiciese algo similar y perder así esta ventaja. Por eso Gosset habría publicado su trabajo bajo un pseudónimo, para no vincularlo con la destilería.

Nos vamos…

Y con esto vamos a ir terminando por hoy.

Hemos visto cómo un espíritu inquieto e inteligente (con ayuda de algunos amigos) supo adaptar la estadística a sus necesidades con el objetivo de mejorar sus estimaciones sin verse limitado por el tamaño muestral reducido que tenía que emplear en sus estudios.

Pero el objetivo no era solo este, sino que también perseguía que la producción no se viese sujeta a variaciones de condiciones ambientales de suelo, clima y cosas así. Dicho de otra forma, tuvo interés en desarrollar métodos robustos frente a la presencia de valores extremos. Aunque el mérito en este punto se lo apuntaría después su amigo Fisher. Pero esa es otra historia…