Modificación de efecto.

La modificación de efecto se produce cuando la magnitud de una variable interfiere sobre el efecto de la exposición sobre el resultado.
En esta entrada vamos a dar otra vuelta de tuerca al asunto de las variables que pueden enturbiar la armoniosa relación de la pareja formada por exposición y efecto, así que todas aquellas mentes sucias que esperaban otra cosa al leer el título pueden pasar al siguiente resultado de Google, que seguro que aciertan con lo que andaban buscando.
Variables de confusión
Ya vimos como existen variables de confusión que se relacionan con el efecto y la exposición y cómo pueden alterar nuestras estimaciones de las medidas de asociación si estas variables no se reparten de forma homogénea entre los grupos de estudio. Hablamos de nuestra puerta trasera, de cómo evitarla y de cómo cerrarla, tanto en los estudios de cohortes como en los de casos y controles.
Modificación de efecto
Pero, en ocasiones, el efecto de la exposición sobre el resultado estudiado no es siempre el mismo, pudiendo variar en intensidad según se modifica el valor o nivel de una tercera variable. Al igual que ocurría con la confusión, lo observamos mejor al estratificar los resultados para hacer el análisis, pero en estos casos no se debe a la distribución desigual de la variable, sino a que el efecto de la exposición se ve realmente modificado por la magnitud de esta variable, que recibe el nombre de variable de interacción o variable modificadora de efecto.
Como es lógico, es fundamental diferenciar entre variable de confusión y variable de interacción. El efecto de la variable de confusión depende de su distribución entre los grupos de estudio. En el caso de estudios experimentales, esta distribución puede ser diferente según se haya producido el reparto al hacer la aleatorización, por lo que una variable puede actuar como confusora en un ensayo y no en otro. Sin embargo, en los estudios observacionales siempre ejercen su efecto, ya que se encuentran asociadas tanto al factor como a la exposición. Cuando encontramos una variable confusora nuestro objetivo será controlar su efecto y estimar una medida de asociación ajustada.
Por otra parte, las variables modificadoras de efecto reflejan una característica de la relación entre exposición y efecto, cuya intensidad depende del ménage à trois que forman con esta tercera variable de interacción. Si pensamos un poco, en el caso de que exista una modificación de efecto no nos interesará calcular una medida ajustada de la asociación, como la que obtendríamos con la prueba de Mantel-Haenszel, ya que no sería representativa del efecto global de la exposición sobre el efecto. Tampoco es buena idea hacer una simple media aritmética de las medidas de asociación que observamos en cada estrato. En todo caso lo que tenemos que hacer es describirla y no tratar de controlarla, como hacemos con las variables confusoras.
Estratificación
Antes de poder decir que existe una variable modificadora de efecto debemos descartar que las diferencias observadas se deban al azar, a confusión o a sesgos de nuestro estudio. Observar los intervalos de confianza de las medidas de estimación nos puede ayudar a descartar el azar, que será más improbable si los intervalos no se solapan. Podemos calcular también si las diferencias entre los estratos son estadísticamente significativas, utilizando para ello es test apropiado a cada diseño de estudio.
¿Y podemos estimar una medida global de la influencia de la exposición sobre el efecto que tenga en cuenta la existencia de una variable de interacción?. Pues claro que podemos, ¿alguien lo dudaba?.
Quizás la forma más sencilla es calcular una medida estandarizada. Para ello comparamos dos medidas diferentes, una que asume que cada elemento de cada estrato de la población tiene el riesgo de los expuestos y otra que asume lo mismo pero de los no expuestos. Se estima así una medida de la asociación en la población global estándar que hemos definido. ¿Confuso?. Veamos un ejemplo.Vamos a seguir aburriendo hasta la extenuación con los pobres fumadores y su enfermedad coronaria. En la primera tabla están los resultados de un estudio que me acabo de inventar sobre tabaco e infarto de miocardio.
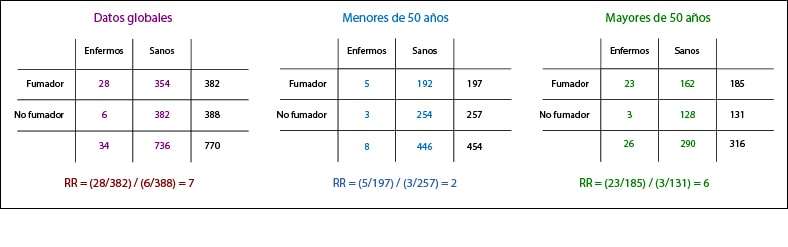
Vemos que, de forma global, los fumadores tienen un riesgo siete veces superior de sufrir infarto que los no fumadores (riesgo relativo, RR = 7). Vamos a suponer que fumadores y no fumadores tienen una distribución de edad semejante, pero que al desglosar los datos en dos grupos de edad los riesgos son diferentes. El RR en menores de 50 años es de 2, frente al de los mayores, cuyo riesgo de infarto es tres veces mayor para los fumadores que para los no fumadores.
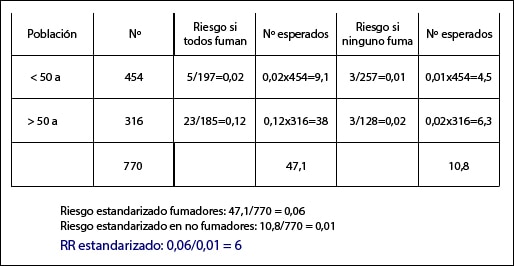
Hacemos los mismos cálculos con los mayores de 50 años y sumamos el total de personas (770), el total de infartos en fumadores (47,1) y en no fumadores (10,8). El riesgo estandarizado en los fumadores de esta población es de 47,1/770 = 0,06. El riesgo estandarizado en no fumadores, 10,8/770 = 0,01. Por último, calculamos el RR estandarizado: 0,06/0,01 = 6. Esto significa que, de forma global, fumar multiplica por seis el riesgo de infarto, pero no olvidemos que este resultado es válido solo para esta población estándar y que no lo sería probablemente para otra población diferente.
Nos vamos…
Solo una cosa más antes de acabar. Como ocurre con el análisis de las variables de confusión, el análisis de la modificación de efecto puede hacerse también mediante regresión, introduciendo en la ecuación obtenida unos coeficientes de interacción que corrigen el efecto. Además, estos coeficientes nos resultan muy útiles porque su significación estadística nos sirve para distinguir entre confusión e interacción. Pero esa es otra historia…
