Tamaño muestral para la estimación de una proporción.

Es curioso cómo los matemáticos tienen formas de decir las cosas para que solo las entiendan ellos (habló el cojo del manco, me diréis, oyendo esta queja de un médico).

Por ejemplo, estaba dándole vueltas a los conceptos de razón y proporción, que son parecidos a veces pero que son cosas diferentes. Y entonces se me ocurrió la genialidad de buscar las definiciones matemáticas, con la ingenua esperanza de aclararme de forma rápida y sencilla.

Pues resulta que, para los matemáticos, una proporción es la igualdad de dos razones. Claro que, para que lo terminemos de entender, nos dicen que una proporción tiene cuatro componentes o términos, llamados extremos (el primero y el último) y medios (el segundo y el tercero). ¿Verdad que con esto ya queda aclarado?

Vamos a ver si sabiendo que es una razón, nos iluminamos un poco. Según la sabia Wikipedia, una razón es una relación binaria entre magnitudes que, en el caso de ser numérica, puede expresarse de forma fraccionaria y, eventualmente, como un decimal. ¡Toma ya!

Parece que tanto razón como proporción están formadas por un cociente de dos cifras. Lo que tiene de particular la proporción es que implica una relación de correspondencia entre el todo y las partes de ese todo. Dicho de forma sencilla, el numerador de una proporción está incluido en el denominador.

Por ejemplo, supongamos que en una población de 80 personas hay 4 de ellas que padecen esa horrible enfermedad que es la fildulastrosis. Diremos que la proporción de enfermos será de 4 dividido entre 80 (este 80 incluye los 4 enfermos) o, lo que es lo mismo, 0,05. También podemos multiplicarlo por 100 y decir que es del 5%.

Esta proporción implica un concepto probabilístico: nos dirá la probabilidad de que, si elegimos un individuo al azar, tenga la enfermedad. Y esa proporción, cuando nos referimos al número de personas en un grupo que padece una enfermedad o factor de riesgo en un momento específico, es lo que denominamos prevalencia.

Estimación de una prevalencia

Supongamos que queremos saber la proporción de personas de nuestra ciudad que padece fildulastrosis. Dicho de otro modo, queremos saber la prevalencia de fildulastrosis en nuestra ciudad.

Lo más exacto sería preguntar uno por uno sobre el estado de salud o enfermedad, pero esto puede plantear algún problema. Supongamos que vivimos en Ciudad de México, con sus más de 8 millones de habitantes. Preguntarles a todos se nos iba a hacer un poco pesado.

Lo que se suele hacer es seleccionar una muestra de individuos que sea representativa de la población diana (los habitantes de la ciudad) y medir la prevalencia en la muestra, más accesible.

Una vez que tengamos el valor muestral, haremos nuestra estimación del valor que tendrá la prevalencia en la población inaccesible, siempre con cierto grado de variabilidad o error, que podemos también determinar.

¿Y cuál es el tamaño muestral necesario para la estimación de una proporción? La respuesta a esta pregunta depende de una serie de factores que trataremos a continuación.

Factores que influyen en el tamaño muestral para la estimación de una proporción

Para calcular el tamaño muestral para la estimación de una proporción debemos establecer, en primer lugar, el nivel de confianza y la precisión que deseamos que tenga nuestra estimación de la prevalencia. Además, el tamaño muestral necesario variará según el valor de esta prevalencia.

El nivel de confianza

Dicho de una forma sencilla, aunque no del todo exacta, el nivel de confianza hace referencia a la probabilidad de que el intervalo de confianza de nuestra estimación incluya el verdadero valor poblacional que no podemos medir directamente.

Lo habitual es elegir una confianza del 95%, con lo que estimaremos un valor puntual con su intervalo de confianza del 95%. Esto se hace utilizando la puntuación estandarizada que deja fuera del intervalo el 5% de la población normal estándar. Este valor es lo que se conoce como Zα, siendo α el nivel de significación (el complementario del nivel de confianza).

Así, si elegimos una confianza del 95%, α valdrá 0,05 y le corresponderá un Z de 1,96 para un contraste bilateral. En la tabla adjunta os muestro algunos de los valores Z más utilizados, aunque pueden calcularse utilizando una distribución normal.

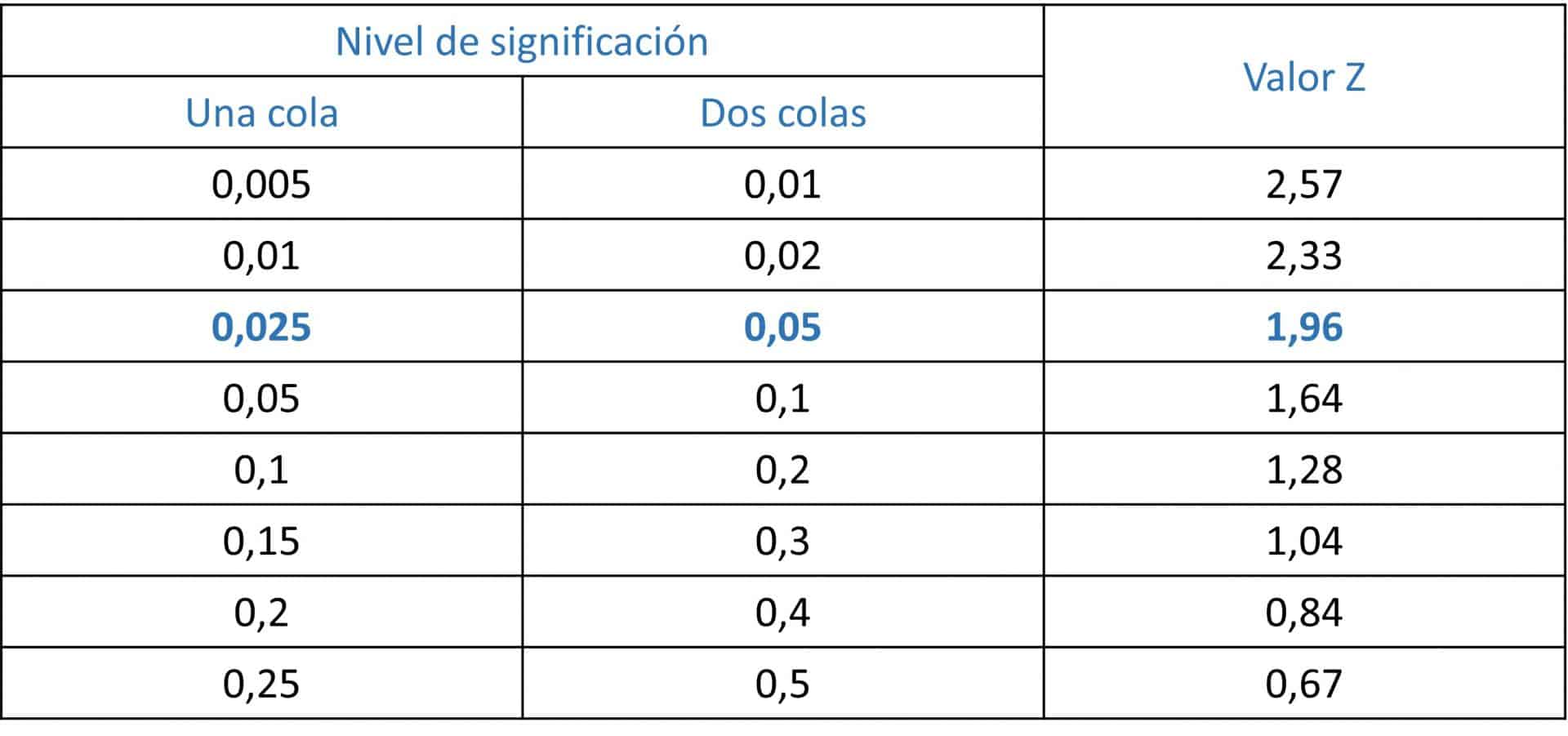
Recordad que esta elección se hace simplemente por convenio y que, según cada caso individual, podemos elegir el nivel de confianza que deseemos. Eso sí, hay que tener en cuenta que el tamaño muestral aumenta de forma directamente proporcional al cuadrado del valor Zα: a mayor nivel de confianza, menor valor de α y mayor Zα, con lo que el tamaño muestral aumentará.

La precisión de la estimación

Como siempre, la precisión se verá reflejada por la amplitud del intervalo de confianza de la estimación.

Lógicamente, querremos hacer una estimación lo más precisa posible, pero hay que tener en cuenta que el tamaño muestral aumenta de forma inversamente proporcional al cuadrado de la amplitud del intervalo. Esto quiere decir que, a menor intervalo, mayor tamaño muestral.

Además, al variar con el cuadrado de la precisión, pequeños aumentos de la precisión de la estimación pueden llevar aparejados un gran aumento de la muestra necesaria para ello.

El valor de la proporción que queremos estimar

Muchos estaréis pensando que esta condición es un poco absurda: si supiésemos el valor de la proporción no tendríamos necesidad de realizar ninguna estimación.

Pero las matemáticas son así de caprichosas. Creo que ya podemos ver la fórmula para calcular el tamaño muestral para la estimación de una proporción, así que os la muestro en la figura adjunta.

Siendo p la proporción de enfermos (prevalencia) y 1-p la proporción de sanos en la población, el tamaño muestral necesario aumenta de forma directamente proporcional con el producto de p(1-p). Necesitamos el valor de la prevalencia, aunque sea aproximado.

Este valor podemos obtenerlo de trabajos previos de nuestra población o poblaciones parecidas. En el caso de que no podamos imaginar cuál puede ser el valor de esta proporción, que valdrá entre 0 y 1, nos iremos al medio, a 0,5. Y esto no es un capricho, como veremos a continuación.

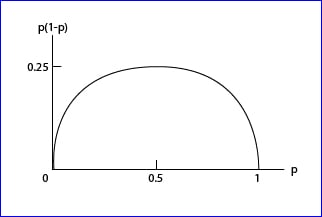
En la figura que os adjunto podéis ver representada la relación de p frente a p(1-p). Como podéis ver, el valor máximo de este producto se alcanza cuando p es igual a 0,5. Esto quiere decir que, para un mismo nivel de confianza y precisión, el tamaño muestral necesario será máximo cuando la proporción poblacional valga 0,5.

Entre 0 y 0,5, el tamaño muestral aumentará, para disminuir después según se evoluciona desde 0,5 a 1. Por eso, si dudas, mejor al medio. Nunca te quedarás corto de tamaño muestral, aunque probablemente emplearás más del necesario.

Una pequeña corrección

Hasta ahora nos hemos movido en el supuesto de una población diana lo suficientemente grande como para considerarla infinita.

En la práctica, podemos asumir que la población es finita cuando es menor de 5000. En estos casos, una vez calculado el tamaño muestral según la fórmula que ya os indiqué, habrá que hacer la corrección que se indica en la misma figura.

Si no hacemos esto, puede ocurrir que el tamaño muestral necesario que obtengamos sea mayor que la población diana, así que mejor realizar la corrección para población finita y disminuir el tamaño de muestra necesario.

Veamos algún ejemplo

Vamos a volver con nuestra temida fildulastrosis. Hemos leído algunos trabajos que dicen que la prevalencia en países similares al nuestro es del 10%. Ahora queremos estimar la prevalencia en nuestra población, con un nivel de confianza del 95% y un intervalo de confianza de ±5%.

Bien, sabemos que p = 0,1, Zα = 1,96 y d = 0,05.

Si sustituimos los valores en la fórmula, tal como se muestra en la figura, veremos que la muestra necesaria es de 138 personas.

Vamos a suponer que desconocemos totalmente la prevalencia probable de enfermedad. En este caso, asumiremos que es del 50%. Los valores de d y Zα no cambian, pero p vale ahora 0,5. Si sustituimos en la fórmula, veremos que necesitamos 384 personas, más que en la ocasión anterior.

Por último, vamos a suponer que queremos saber la prevalencia en un grupo de 120 personas y no nos apetece preguntarles a todas si están enfermas o sanas. Procederíamos como en el primer supuesto, obteniendo un tamaño de muestra de 138, más de las que tenemos.

Realizamos la corrección para muestra finita según la fórmula que ya conocemos y obtenemos un tamaño muestral corregido de 64 personas.

Nos vamos…

Hemos visto en esta entrada cómo calcular el tamaño muestral para la estimación de una proporción.

También hemos visto que el tamaño muestral para una misma estimación puede variar según se trate de una población diana infinita o finita, más pequeña. Esto es así porque podemos hacer estimaciones bastante precisas con un tamaño muestral asequible, pero para que esto funcione tiene que cumplirse una condición: la muestra debe ser representativa de la población de la que procede. Pero esa es otra historia…