Media geométrica
La media geométrica se utiliza cuando los valores de la distribución de datos cambian de forma multiplicativa, y no aditiva. Esto la hace ideal para promediar datos de progresión geométrica, como razones, interés compuesto en economía o crecimientos de bacterias en microbiología.
Ya sabemos que la media aritmética es la más famosa de las medidas de tendencia central de una distribución, por lo que a nadie debe extrañarle que esté implicada en tantos procedimientos estadísticos y matemáticos.
Sin embargo, la media tiene un pequeño defecto: se deja arrastrar con facilidad por la presencia de valores extremos en la distribución de datos. Por decirlo de una forma un poco más técnica, es poco robusta frente a la presencia de valores extremos.
Para estos casos puede ser más conveniente utilizar otras medidas de tendencia central que sean más robustas. Hoy vamos a hablar de una de ellas, la media geométrica. Y, para hacerlo, vamos a suponer que nos hemos convertido en microbiólogos.
Un pequeño experimento
Imaginemos que estamos en nuestro laboratorio buscando la manera de enriquecer un medio de cultivo para detectar con más facilidad la presencia de Fildulastrum fildulastrii, el germen causal de esa terrible enfermedad que es la fildulastrosis.
Vamos a sembrar una serie de placas con los bichos y, para comparar las placas con los distintos medios de enriquecimiento, vamos a calcular la media de los bichos que nos crecen en cada serie.
Por ejemplo, tenemos cinco placas que hemos enriquecido con un medio determinado y contamos las colonias que obtenemos en cada una: 1.000, 100, 100.000, 100 y 1.000.
Ahora yo os pregunto: ¿cuál es el crecimiento medio con este medio de cultivo?
Los menos reflexivos de vosotros os apresuraréis a calcular la media aritmética, que es de 20.440 colonias por placa.
Y entonces yo os preguntaría: ¿de verdad creéis que 20.440 es una buena medida de tendencia central para esta distribución de valores? Si reflexionáis un poco veréis que no lo es. El problema es que tenemos un valor extremo, el 100.000, y la media aritmética se ve irresistiblemente arrastrada hacia él.
Para calcular una medida de tendencia central más acertada necesitamos algo más robusto frente a la presencia de los valores extremos. Concretamente, necesitamos recurrir a la media geométrica.
La media geométrica
La media geométrica de una cantidad n de números es la raíz enésima del producto de todos los números.
Para aquellos que sepan apreciar la belleza del lenguaje matemático, lo dicho anteriormente puede expresarse con la siguiente fórmula:
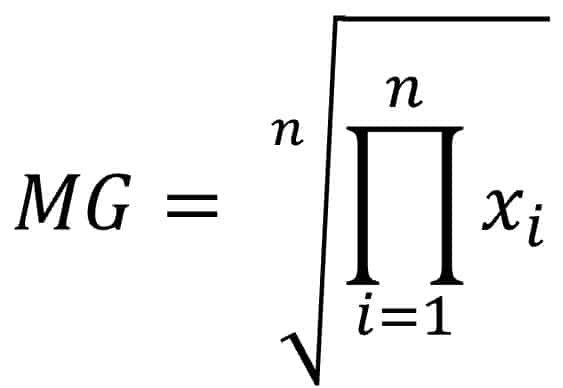
Suele utilizarse la media geométrica cuando los valores de la distribución cambian de forma multiplicativa, y no aditiva. Esto la hace ideal para promediar datos de progresión geométrica, como razones, interés compuesto en economía y, como en nuestro caso, crecimientos de bacterias en microbiología.
Por ejemplo, si una empresa ha crecido en los últimos 5 años un 15%, 22%, 14%, 18% y 12%, lo correcto sería calcular la media geométrica para dar una medida de crecimiento medio para los 5 años. Podemos utilizar el programa R para calcularlo:
(15*22*14*18*12)^0,2 = 15,84.
El crecimiento medio es del 15,84%. Os aclaro, por si acaso, que elevar a 0,2 (1/5) es lo mismo que hacer la raíz quinta.
Apliquémoslo ahora a nuestro problema:
(1000*100*100000*100*1000)^0,2 = 1.000.
Ahora sí, 1000 nos parece una medida de tendencia central más acertada para esta distribución.
Una relación inesperada
Para ir terminando esta entrada de hoy, vamos a ver una de esas relaciones inesperadas que nos ofrece de vez en cuando la magia de las matemáticas. Y es que resulta que la media geométrica está muy relacionada con los logaritmos. Veámoslo.
Aunque pueda parecer extraño, Napier inventó los logaritmos en el siglo XVII para facilitar los cálculos matemáticos. La forma más sencilla, a mi humilde entender, de decir qué es un logaritmo es decir que el logaritmo de un número indica el exponente al que hay que elevar un número (la base) para obtener el número original.
Veamos un ejemplo para entenderlo mejor. El logaritmo base 10 de 100 es igual a 2:
log10(100) = 2
Esto es así porque 2 es el número al que hay que elevar la base (10) para obtener el número original (100).
Resulta que el producto de n números es equivalente a la suma de sus logaritmos, así que el logaritmo de la media geométrica será igual a la media aritmética de la suma de logaritmos.
De esta manera, para calcular la media geométrica, podemos:
1. Sumar los logaritmos de los números de la distribución.
2. Dividirlos por el total de números (n) para calcular la media aritmética.
3. Calcular el antilogaritmo o, lo que es lo mismo, la función exponencial para obtener la media geométrica.
Veamos como resolveríamos nuestro ejemplo con este otro método, utilizando para ello el programa R:
media.geometrica <- exp(mean(log(c(1000, 100, 100000, 100, 1000))))
El resultado sería el que ya conocemos, 1.000.
Nos vamos…
Y aquí lo vamos a dejar por hoy.
Hemos visto algunos de los usos de la media geométrica, que no debemos confundir con otra medida de tendencia robusta muy similar, la media armónica. La media armónica es más utilizada en situaciones en las que hay que promediar trayectos de igual longitud con diferentes tiempos, así como para promediar múltiplos o cocientes. Además, existen otras medidas de tendencia central robustas de las que no hemos hablado nada, como la media recortada, la winsorizada, la ponderada, etc. Pero esa es otra historia…
