Tamaño muestral para comparación de dos medias.

Que nadie se piense cosas raras al leer el título de esta entrada. Hoy no vamos a hablar de ropa. Las medias de las que vamos a hablar son, como ya imaginaréis, medias aritméticas.

Vimos en una entrada anterior cómo podíamos estimar el valor medio de una variable aleatoria, como la cifra de colesterol en sangre, en una población sin necesidad de tener que medir el colesterol a todos los individuos de la población.

Para ello, seleccionábamos una muestra de individuos representativos de la población y les medíamos el colesterol, obteniendo la media en la muestra. Después, a partir de esa media, ya podíamos estimar entre qué valores podía encontrarse el valor medio de la población, que es inalcanzable para nosotros.

La pregunta clave era cuántos individuos teníamos que incluir en la muestra. Ya vimos cómo el número necesario dependía del nivel de confianza con el que deseásemos hacer la estimación, de su precisión y de la variabilidad de la variable en la población.

Comparación de dos medias

En el caso anterior estimábamos el valor de una variable continua en una población a partir de su valor en la muestra seleccionada.

Ahora pensemos que las características de esa variable puedan diferenciarse según las categorías de otra variable. Por ejemplo, supongamos que queremos saber si los valores medios de colesterol son iguales en niños y en niñas.

En este caso deberíamos seleccionar dos muestras, una de niñas y otra de niños, calcular los valores medios de colesterol en las dos muestras y compararlos para ver si la diferencia que observemos entre las determinaciones puede ser debida al azar. Para esto podremos utilizar varias pruebas, como la de la t de Student, que incluso funcionará bien aunque la muestra no sea muy grande y no conozcamos la varianza de la variable en la población.

Pero, ¿cuántos niños y cuántas niñas tendremos que selecciona? Seguid leyendo y lo veréis.

Tamaño muestral para la comparación de dos medias

Hay varios factores que nos van a influir en el tamaño muestral necesario para poder comparar dos medias. En primer lugar, tendremos que decidir si nos basta con averiguar que las dos medias son diferentes o si queremos precisar si una de ella es mayor o menor que la otra. Esto es, deberemos definir la dirección del contraste, unilateral o bilateral.

Además, tenemos que establecer el nivel de confianza y la potencia que deseemos, y el tamaño de la diferencia entre las dos medias que queremos ser capaces de detectar estadísticamente. Por último, tenemos que conocer el valor de la varianza de la variable en los dos grupos en la población.

Veamos cada uno de estos factores.

Contraste unilateral o bilateral

Aunque solo sea por azar, seguro que cuando calculemos los valores medios de las dos muestras obtendremos resultados diferentes.

Estaremos interesados, cuando vayamos a hacer el contraste de hipótesis, en saber cuál es la probabilidad de que esta diferencia se deba al azar. Si es muy alta, asumiremos que las dos medias son iguales y la diferencia observada se debe a la casualidad. Si es muy baja (habitualmente < 0,05), asumiremos que existe una diferencia que probablemente no se deba al azar (la diferencia será estadísticamente significativa).

Llegados a este momento, decidiremos si nos basta con saber que las medias son diferentes o si queremos determinar si una de ellas es específicamente mayor o menor que la otra. En el primer caso se trataría de un contraste bilateral, mientras que en el segundo haríamos uno unilateral.

Habitualmente se considera más correcto realizar un contraste bilateral. Sin embargo, si tenemos información que nos permita afirmar cuál puede ser mayor, el contraste podrá ser unilateral. Este último es menos conservador, lo que quiere decir que es más fácil alcanzar la significación estadística, aunque esta no debe ser la razón para elegirlo.

El nivel de confianza

Lo habitual es elegir una confianza del 95%, con lo que estimaremos un valor puntual para la diferencia de medias con su intervalo de confianza del 95%. Así, obtendremos el valor de la distribución normal estándar que deja fuera, por cada lado, a un 0,025 (2,5%) de la población. Este valor es lo que se conoce como Zα, siendo α el nivel de significación (el complementario del nivel de confianza).

Por ejemplo, si elegimos una confianza del 95%, α valdrá 0,05 y le corresponderá un Z de 1,96 para un contraste bilateral. Esto podemos calcularlo con un programa estadístico o recurrir a alguna de las múltiples tablas disponibles en Internet y en libros de estadística.

La potencia del estudio

La potencia del estudio es la probabilidad de que se pueda detectar la diferencia, si esta existe realmente en la población.

Lo más habitual es seleccionar una potencia del 80% (β = 0,2) o del 90% (β = 0,1). A partir de este valor, y de forma similar a como hacíamos con α, calcularemos el valor de Zβ que utilizaremos, como veremos más adelante, para calcular el tamaño muestral.

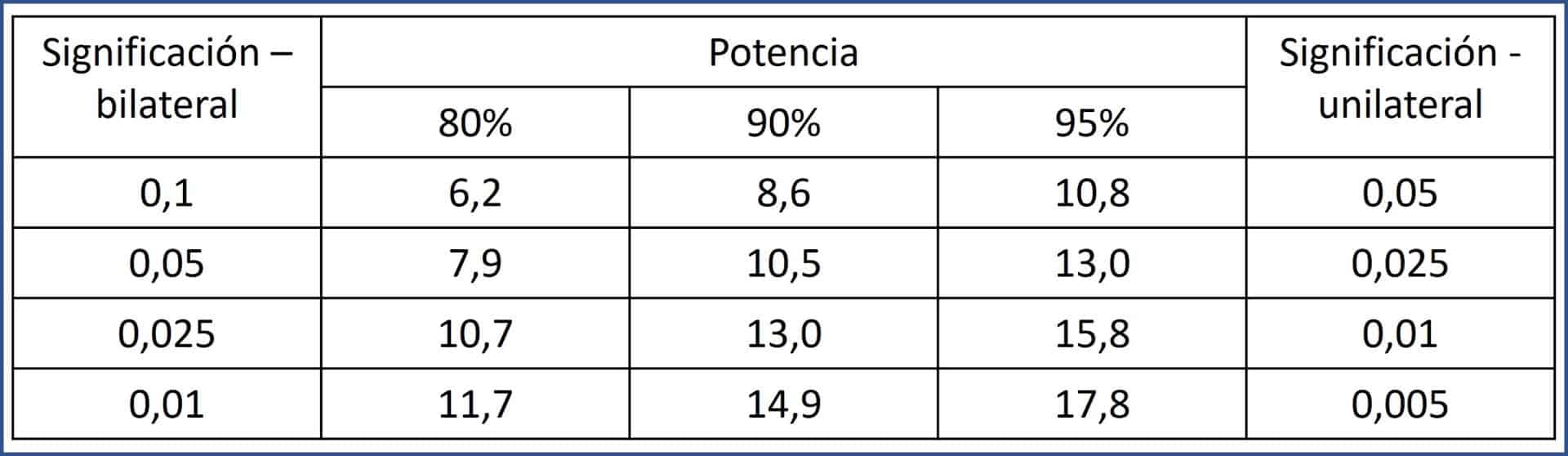
Como veremos en seguida, los valores de Zα y Zβ se suman y se elevan al cuadrado para calcular un valor K, que es el que utilizamos con la fórmula del tamaño muestral.

En la tabla adjunta podéis ver los valores de K utilizados con más frecuencia en función del nivel de significación, la potencia y el tipo de contraste.

La precisión del estudio

Ya lo hemos dicho, queremos saber qué diferencia entre las dos medias queremos ser capaces de detectar.

Como es lógico, nos gustará hacer estudios más precisos, pero esto tiene un coste en el tamaño muestral necesario, por lo que tendremos que buscar un punto medio de equilibrio.

La varianza en los dos grupos

Este es un valor que debemos conocer o estimar para poder calcular el tamaño muestral.

Como es lógico, cuánto mayor sea la dispersión de la variable en la población, más difícil será calcular el tamaño muestral para un mismo nivel de confianza y precisión, lo que se traducirá en un tamaño muestral necesario más grande.

Tamaño muestral para la comparación de dos medias

Creo que es el momento de conocer la fórmula que nos va a permitir calcular el tamaño muestral necesario para poder comparar dos medias. Podéis verla a continuación.

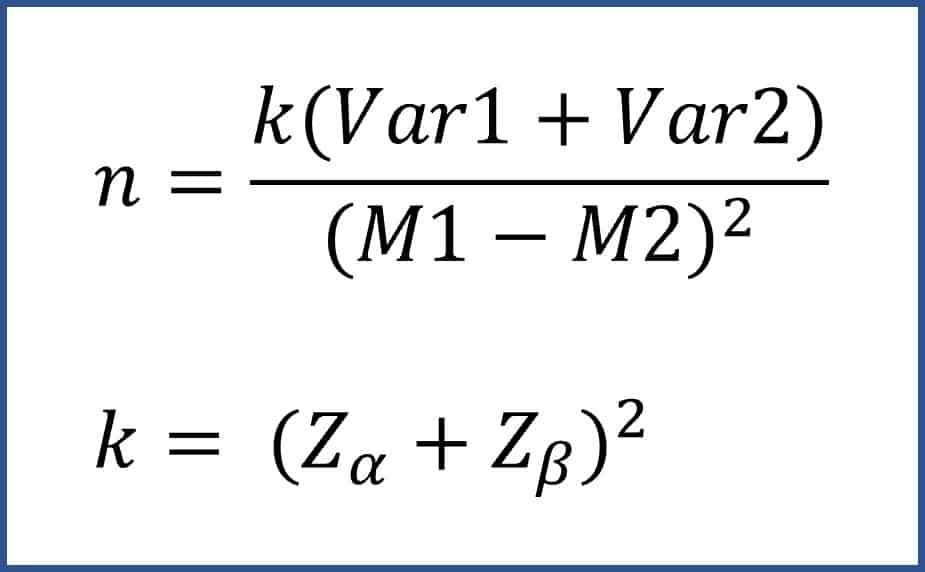
Como podéis ver, el tamaño muestral aumenta de forma proporcional al cuadrado de α y β. Esto quiere decir que K (y, por tanto, el tamaño de la muestra) será mayor cuánto más bajo sea el nivel de confianza o más alta sea la potencia del estudio. Lo mismo puede decirse con la varianza del estudio, también en el numerador. En este caso podemos sumar las dos varianzas o, si se prefiere, calcular previamente la varianza común.

Además, la muestra necesaria aumenta de forma inversamente proporcional al cuadrado de la precisión. Esto quiere decir que, cuanto menor sea la diferencia que queramos detectar (mayor precisión), mayor será la muestra necesaria. Además, al variar con el cuadrado de la diferencia detectable, pequeñas disminuciones de esta llevarán aparejados grandes aumentos del tamaño de la muestra.

Veamos un ejemplo

Sigamos con nuestro ejemplo del colesterol sérico.

Supongamos que disponemos de un estudio totalmente ficticio que nos dice que la desviación estándar del colesterol es igual en niños y niñas, de 35 mg/dl.

Ahora queremos saber cuántos participantes necesitamos para comparar las medias en los dos géneros con un nivel de confianza del 95%, una potencia del 80% y un contraste bilateral. Por último, queremos ser capaces de detectar una diferencia de 10 mg/dl en los valores medios de colesterol.

Si sustituimos en la fórmula, K = 7,9, Var1 = Var2 = 35² y la diferencia de medias a detectar es de 10 mg/dl. Si resolvemos la ecuación veremos que necesitamos 193 participantes en cada grupo para hacer la estimación que deseamos.

Podéis verlo en la aplicación adjunta. Os animo a variar las diferentes opciones para que veáis cómo influyen sobre el tamaño muestral necesario.

Nos vamos…

Y con esto acabamos por hoy.

Aunque calcular el tamaño muestral para la comparación de dos medias es bastante sencillo, os aconsejo no hacerlo a mano y emplear una de las calculadoras disponibles en Internet.

Hemos visto cómo comparar las dos medias cuando la variable es cuantitativa. Como es lógico, también podemos calcular la muestra necesaria para comparar dos proporciones cuando estemos trabajando con una variable categórica. Pero esa es otra historia…