Importancia clínica.

Se describe cómo debe valorarse la importancia clínica de los resultados de un estudio, sin limitarse solo a su significación estadística.
Los resultados y la validez de cualquier trabajo epidemiológico están siempre sometidos a dos temibles peligros: el error aleatorio y los errores sistemáticos.
Los errores sistemáticos, sesgos para los amigos, están relacionados con defectos del diseño del estudio en cualquiera de sus fases, por lo que debemos ser cuidadosos a la hora de evitarlos para no comprometer la validez de los resultados.
El error aleatorio es harina de otro costal. Es inevitable y se debe a variaciones que no podemos controlar y que se producen durante los procesos de medición y recogida de datos, alterando la precisión de nuestros resultados. Pero que nadie desespere: no podremos evitar el azar, pero sí podemos controlarlo (dentro de unos límites) y medirlo.
Supongamos que medimos la diferencia de saturación de oxígeno en extremidad superior e inferior en veinte recién nacidos sanos y calculamos la media: 2,2%. Si repetimos el experimento, incluso con los mismos neonatos, ¿qué valor obtendremos?. Con toda probabilidad, cualquiera menos 2,2% (aunque se parecerá bastante si hemos hecho las dos tomas en las mismas condiciones). Ese es el efecto del azar: la repetición tiende a producir resultados diferentes, aunque cercanos al valor verdadero que queremos medir.
El error aleatorio puede reducirse aumentando el tamaño de la muestra (con cien niños en lugar de veinte las medias serán más parecidas si repetimos el experimento), pero nunca nos libraremos completamente de él. Para empeorar las cosas, ni siquiera queremos saber la media de la diferencia de saturación en estos veinte, sino en la población de la cual proceden. ¿Cómo salimos de este laberinto?. Lo habéis adivinado, utilizando intervalos de confianza.
Significación estadística
Cuando establezcamos la hipótesis nula de que no hay diferencias entre tomar la saturación en la pierna o en el brazo y realicemos la comparación de las medias con el test estadístico apropiado, el valor de la p nos indicará la probabilidad de que la diferencia encontrada se deba al azar. Si p < 0,05, asumiremos que la probabilidad de que la diferencia se deba al azar es tan pequeña como para rechazar con tranquilidad la hipótesis nula y abrazar la hipótesis alternativa: no es lo mismo tomar la saturación en la pierna que en el brazo.
Por otro lado, si la p no es significativa, no podremos rechazar la hipótesis nula, pero siempre nos quedará la duda de cuál habría sido el valor de p con 100 niños, o con 1000. Es posible que entonces la p sí hubiese alcanzado significación estadística y hubiésemos podido rechazar H0.
Si calculamos el intervalo de confianza de nuestra variable tendremos el rango en el cual se encuentra su valor real con una probabilidad determinada (habitualmente 95%). Esto nos informará de la precisión del estudio. No será lo mismo obtener como resultado que la diferencia de saturación es de 2 a 2,5% que de 2 a 25% (en este caso, el estudio habría que valorarlo con desconfianza aunque la p tuviese cinco ceros).
Importancia clínica
¿Y qué pasa si la p no es significativa?. ¿Podemos sacar conclusiones del estudio?. Pues eso dependerá en gran medida de la importancia de lo que estemos midiendo, de su impacto clínico. Si consideramos una diferencia de saturación significativa desde el punto de vista clínico del 10% y el intervalo está por debajo, aunque la p sea significativa el impacto clínico del hallazgo será mínimo. Pero lo bueno es que este razonamiento puede también hacerse al revés: intervalos no significativos pueden tener gran impacto si alguno de sus límites entra en la zona de importancia clínica.
Veámoslo con unos ejemplos en el gráfico siguiente, en el que se ha supuesto una diferencia importante desde el punto de vista clínico del 5% en la saturación de oxígeno (perdonadme los neonatólogos, pero de la saturación solo sé que la mide una máquina que muchas veces no capta bien y pita).
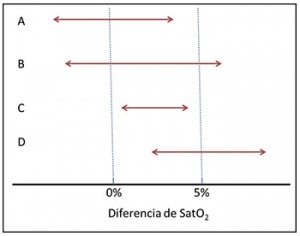
El estudio B tampoco es estadísticamente significativo, pero clínicamente podría ser importante, ya que el límite superior del intervalo cae en la zona de relevancia clínica.
Si aumentásemos la precisión del estudio (aumentando la muestra), ¿quién nos asegura que el intervalo no se podría estrechar y quedar por encima del nivel nulo, alcanzando significación estadística? En este caso la duda no parece muy trascendente porque la variable que estamos midiendo como ejemplo es un poco chorra, pero pensad cómo cambiaría esto si estuviésemos considerando una variable más dura, como mortalidad.
Los estudios C y D alcanzan significación estadística, pero solo los resultados del D son clínicamente importantes. El estudio C mostraría una diferencia, pero su impacto clínico y, por tanto, su interés son mínimos.
Nos vamos…
Así que, como veis, hay ocasiones en las que un resultado con una p no significativa puede proporcionar información de interés desde el punto de vista clínico, y viceversa. Además, todo esto que hemos comentado es importante para entender el planteamiento de los ensayos de superioridad, equivalencia y no inferioridad, pero esa es otra historia…
