Árboles de decisión combinados.

Los árboles de decisión simples tienen el problema de ser menos precisos que otros algoritmos de regresión o clasificación, además de ser poco robustos ante pequeñas modificaciones de los datos con los que se elaboran. Se describen algunas técnicas para elaborar árboles de decisión combinados, como las de agregación por remuestreo y los bosques aleatorios, que tienen como objetivo mejorar la exactitud de las predicciones y evitar el sobreajuste de los modelos.
En el corazón de la helada y lejana Invernalia se alzaban los majestuosos arcianos, árboles blancos de hojas rojas y rostros tallados en su corteza. Estos árboles sagrados estaban impregnados de una magia sobrenatural y eran venerados como portadores de la memoria ancestral. Se dice que, a través de ellos, los hijos del bosque y los caminantes blancos podían espiar a los vivos.
Así que estos árboles místicos no solo guardaban secretos antiguos, sino que, al igual que nuestros árboles de decisión, tenían la habilidad de «predecir» y «decidir» el curso de eventos cruciales en la trama del tiempo. Los Stark buscaban consejo en estos árboles antes de tomar grandes decisiones, de forma parecida a cómo nosotros, hoy en día, consultamos nuestros propios árboles de decisión en el mundo de la ciencia de datos.
¿Quién no querría un árbol en su patio trasero que le susurrase secretos y le guiase en tiempos de incertidumbre? Por suerte, aunque los arcianos ya no existen en nuestro mundo, sí que tenemos nuestros místicos árboles de decisión. Aunque no son de madera ni tienen hojas rojas, los árboles que veremos en esta entrada, desde el solitario árbol de decisión hasta los complejos y densos bosques aleatorios y otras técnicas de árboles de decisión combinados, pueden ayudarnos a navegar por el intrincado bosque de los datos para hacer predicciones y orientar nuestras decisiones.
Cada tipo de árbol en el mundo del análisis de datos tiene su propio encanto y propósito, al igual que cada arciano tenía su lugar sagrado en los bosques de Invernalia. Así que, si alguna vez os habéis preguntado cómo pueden ayudarnos a «predecir» el futuro, seguid leyendo y descubriremos los secretos que guardan.
El planteamiento del problema: árboles de decisión combinados
Vimos en una entrada anterior cómo los árboles de decisión dividían recursivamente el espacio de las variables predictoras para poder estimar o predecir el valor de la variable de respuesta objetivo, que puede ser tanto numérica (árboles de regresión) como nominal (árboles de clasificación).
Además, permitían, de forma relativamente sencilla, hacer una visualización e interpretación de los datos. El problema de los árboles de decisión sencillos es que no suelen alcanzar valores de precisión tan altos como otros algoritmos de regresión o clasificación, además de ser poco robustos en el sentido de que pequeñas variaciones en los datos o en la selección de las variables pueden dar lugar a cambios grandes en los árboles que se construyen y en su desempeño.
Poniendo un poco de imaginación en el asunto, podemos ver estos árboles simples, con poca capacidad de predicción, como una serie de bloques que podemos combinar de diversas maneras para obtener un modelo mucho más potente y preciso. Estos son los modelos de árboles de decisión combinados, que demuestran otro caso de aplicación de aquel viejo aforismo de que la unión hace la fuerza.
En esta entrada vamos a hablar de tres tipos de árboles de decisión combinados: los que se construyen mediante técnicas de agregación por remuestreo, los llamados bosques aleatorios y los que aprenden de sus predecesores para potenciar su rendimiento.
No os preocupéis, la cosa no es tan exótica como parece por el párrafo anterior. Como veremos, se trata de combinar otras técnicas de estadística y ciencia de datos para producir muchos árboles que funcionen mejor que el original.
Agregación por remuestreo (bagging)
Hasta ahora he hecho un esfuerzo por ser fiel a la lengua de Cervantes y me he mantenido con el término en castellano, pero casi en todos los sitios donde se hable de estos árboles se empleará el término en inglés “bagging”. En realidad, bagging no es una palabra como tal, sino la abreviatura de bootstrap aggregation.
Ya hablamos de las técnicas de bootstrapping o remuestreo en una entrada anterior, así que podéis leerla si os apetece refrescar el tema. El método de bagging (me vais a permitir que utilice el término en inglés) construye árboles de decisión combinados agregando árboles y utilizando técnicas de bootstrap, como su nombre indica. Veamos cómo.
El equilibrio entre sesgo y varianza
Cuando estamos desarrollando cualquier algoritmo de regresión o clasificación, siempre nos preguntamos cómo son estas dos características del algoritmo: el sesgo y la varianza.
Dicho de forma sencilla, el sesgo es la tendencia del modelo a cometer errores sistemáticos debido a suposiciones simplificadas sobre la naturaleza del problema. Un modelo con alto sesgo no tiene la capacidad de captar la complejidad de los datos. Por ejemplo, un modelo lineal simple no podrá captar adecuadamente la relación de un conjunto de datos que sigan una tendencia cuadrática. Este modelo tendrá un sesgo elevado, habrá un ajuste del modelo por debajo del óptimo y sus predicciones tendrán un error elevado.
Por su parte, la varianza se refiere a la sensibilidad del modelo a pequeñas fluctuaciones en el conjunto de datos con el que se elabora, los datos de entrenamiento. Un modelo con alta varianza hace que, no solo capte los patrones relevantes de los datos, sino que también se adapte demasiado bien a los datos particulares utilizados y aprenda el ruido o las peculiaridades específicas de esos datos. Esto producirá un sobreajuste (overfitting): el modelo funcionará muy bien con los datos de elaboración, pero no sabrá realizar predicciones correctas cuando lo enfrentemos con nuevos datos.
El sesgo y la varianza están inversamente relacionados en lo que se conoce como el compromiso sesgo-varianza (bias-variance trade-off). Un modelo con bajo sesgo tiende a ser muy flexible y capaz de capturar complejidades en los datos, pero esto también lo hace susceptible a tener alta varianza. Por lo tanto, es esencial encontrar un equilibrio adecuado entre el sesgo y la varianza para lograr un modelo que generalice bien y tenga un buen rendimiento tanto en los datos de entrenamiento como en datos nuevos.
Este problema se presenta con los árboles de decisión simples que, como ya hemos mencionado, son muy poco robustos frente a pequeñas variaciones de los datos. O sea, tienen una alta varianza y tendencia al sobreajuste.
El bagging es una de las técnicas que nos permite controlar este equilibrio y reducir la varianza durante el entrenamiento del algoritmo. Detrás de esta metodología subyace una idea bastante sencilla.
Imaginad que, de una población determinada, hemos extraído 10 muestras y hemos medido una determinada variable cuantitativa. Cada una de estas muestras tendrá su media, con valores más o menos similares, y, vamos a asumir, la misma varianza, la poblacional.
Ahora podemos usar esta distribución muestral y tomar los resultados de las 10 muestras y hacer un promedio con ellas. La media global será el promedio de las 10 medias individuales, pero la varianza global será igual a la varianza poblacional dividida por el tamaño muestral (10 muestras, en este caso).
O sea, que si tenemos un conjunto de observaciones de la misma población, podemos promediarlas para obtener su media y su varianza, de forma que esta última será menor que la de cada conjunto por separado.
Este es el principio que está detrás del bagging, promediar muchos árboles para obtener una predicción precisa y disminuir la varianza. El problema aquí es evidente: habitualmente no disponemos de múltiples conjuntos de datos de la población. Muy bien, este pequeño inconveniente podemos solventarlo fabricando múltiples muestras a partir de la muestra disponible mediante técnicas de bootstrap o remuestreo.
Cada muestra de bootstrap se obtiene seleccionando aleatoriamente, con reemplazo, ejemplos del conjunto de datos original, de modo que cada muestra puede contener duplicados y puede omitir algunos ejemplos originales. Una vez obtenidas las muestras, se entrena un árbol de decisión simple independiente con cada una de ellas.
De esta manera, habremos elaborado un número N de árboles de decisión, cada uno con poco sesgo y mucha varianza. Haciendo un promedio de las predicciones de estos N árboles podemos conseguir una predicción con una varianza mucho menor, o sea, con menos sobreajuste, mejorando la capacidad del modelo para generalizar sus predicciones a datos nuevos.
Y esto no solo sirve para árboles de regresión, sino también para árboles de clasificación. En estos casos, tomamos las predicciones de los cientos o miles de árboles que elaboremos y hacemos una especie de concurso, premiando la categoría predicha con más frecuencia entre el conjunto total de predicciones.
Un ejemplo práctico
Ya vimos cómo hacer un árbol de decisión simple en una entrada anterior, usando para el ello el programa R y el conjunto de datos “mtcars”, muy utilizado para este tipo de ejemplos, que contiene información sobre diferentes modelos de automóviles y sus características. Incluye 32 filas (una por cada modelo) y 11 columnas que representan diversas características de los automóviles, como la eficiencia del combustible (mpg), el número de cilindros (cyl), la cilindrada (disp), la potencia del motor (hp), la relación de ejes traseros (drat), el peso (wt), etc.
En este caso, vamos a predecir la eficiencia del combustible (millas por galón, mpg) en función del resto de las variables. Los que gusten de ir hasta el fondo del asunto, pueden descargarse el script completo de R en este enlace.
Utilizando la librería randomForest de R, el comando para generar el modelo admite una serie de parámetros, como la variable dependiente y las independientes, el conjunto de datos utilizados y dos parámetros para decidir cuántos árboles generamos y cuántas variables se consideran en cada nodo de decisión del árbol. En el caso del bagging, se consideran todas las variables, pero esto cambia con otros tipos de árboles de decisión combinados, como veremos más adelante.
En nuestro caso le pedimos que nos haga 100 árboles y, como es lógico, que use todas las variables predictoras.
R construye el modelo y nos informa de que incluye 100 árboles, que ha tenido en consideración 10 variables en cada nodo, que la media de los cuadrados de los residuos es de 6,55 y que el modelo explica un 81,4% de la varianza de la variable dependiente. ¡No está nada mal! Pensad que esto sería el equivalente a un modelo de regresión con un R2 de 0,81.
Ahora seguro que a todos os gustaría dibujar el árbol, pero, pensadlo un poco… ¿cómo podemos dibujarlo, si es la combinación de 100 árboles distintos? La respuesta es que no podemos. Acabamos de perder una de las ventajas de los árboles, su fácil interpretación gráfica, a cambio de mejorar sus predicciones cuando lo enfrentemos a nuevos datos. Ya veis que, en estadística y ciencia de datos es frecuente que, para poder mejorar una característica, tengamos que renunciar siempre a algo.
Pero no desesperéis, tenemos un recurso que puede ser similar o, incluso, mejor que la representación gráfica: la importancia de cada variable.
Unas importan más que otras
Como los animales en la granja de Orwell, todas las variables son iguales, pero unas más que otras. No todas tienen la misma influencia o utilidad para ayudar al modelo a hacer predicciones exactas.
Cuando os hablé más arriba de los parámetros de la función randomForest(), me dejé uno sin explicar, el parámetro importance. Si le damos a este parámetro el valor True, el modelo calcula y guarda medidas que indican cuán importantes son las diferentes variables en la predicción de la variable objetivo.
Para ello, el algoritmo va alternando entre las distintas variables probando cuál de ellas reduce más la función de error cuando es utilizada en un determinado nodo de división del árbol. Suelen emplearse para ello el error cuadrático medio para los árboles de regresión y la reducción media en la impureza de Gini para los árboles de clasificación, como vimos en la entrada de los árboles de decisión simples.
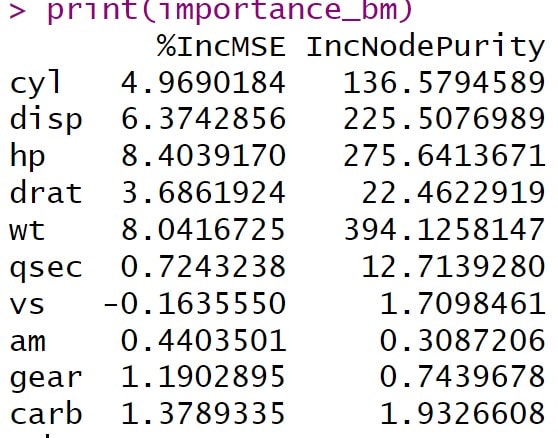
El programa R nos da una tabla con las variables predictoras y dos columnas, el incremento del error cuadrático medio y el incremento de la pureza del nodo (ahora veremos porqué nos da esta segunda columna, aunque sea un árbol de regresión). Podéis ver el resultado en la tabla adjunta.
Vamos primero con el porcentaje de incremento del error cuadrático medio. La variable hp, la potencia del vehículo, es la que tiene el valor más alto, 8,4%, lo que sugiere que es la más importante para predecir la variable dependiente mpg. Al hacer la permutación aleatoria de las variables, la permutación de hp aumenta el error del modelo un 8,4%, lo que sugiere que es una variable importante.
Seguidamente, vemos que wt (8,04%) y disp (6,37%) tienen también un alto impacto en la predicción de mpg, siendo las variables más importantes después de hp. Por otro, la variable vs tiene un valor negativo, lo que indica que su exclusión mejora ligeramente el rendimiento del modelo, y las variables qsec y am tienen valores próximos a 0. Aunque estos pequeños efectos pueden ser debidos al azar, sugerirían que estas variables no son importantes o incluso podrían ser ruido para este modelo específico.
Vemos que R nos ofrece también la columna con los incrementos de pureza del nodo al permutar las variables. En un árbol de regresión, como es nuestro caso, se refiere a la reducción de la varianza dentro de los nodos, por lo que se interpreta de manera similar a la primera columna.
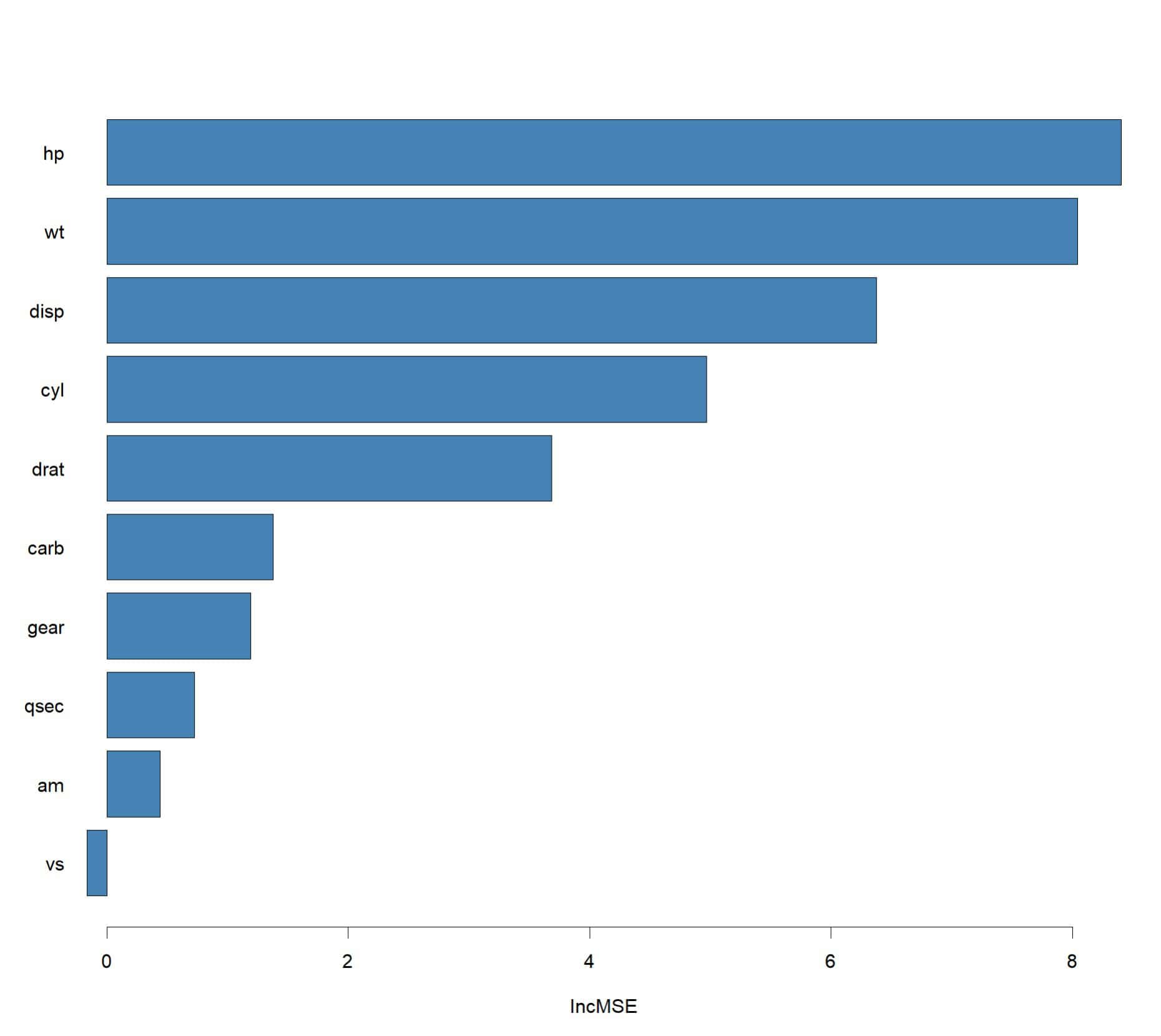
Por último, como podéis ver en la figura anterior, podemos representar gráficamente la importancia de las variables. No podemos dibujar el árbol, pero esta interpretación de la importancia de cada variable me parece un buen complemento para valorar el modelo.
Bosques aleatorios
Ya hemos visto cómo el bagging es una técnica que nos permite disminuir la varianza del modelo y mejorar su capacidad de generalizar al disminuir el sobreajuste. Pero hay un pequeño defecto en el que no hemos pensado hasta ahora.
Supongamos que hay una variable dentro del conjunto de datos que es altamente predictiva de la variable objetivo del modelo. Cuando construyamos múltiples árboles mediante bagging, la mayoría usarán esta variable en el nodo más alto del árbol. Como consecuencia, todos los árboles se parecerán bastante y sus predicciones también. Para decirlo como si supiésemos de qué estamos hablando, los árboles estarían altamente correlacionados, al igual que sus predicciones.
¿Cuál es el problema? Hacer un promedio de predicciones correlacionadas no permite conseguir una reducción de la varianza tan grande como a la que se puede llegar si no existe correlación. Para solucionar este problema se inventaron los bosques aleatorios, aunque todo el mundo los conoce mejor por su término en inglés, random forest.
Los random forest van un paso más allá que los árboles de bagging. Hacen el remuestreo igual para elaborar múltiples árboles pero, en cada árbol concreto, cuando llegan a un nodo, en lugar de considerar todas las variables predictoras, utilizan un subconjunto aleatorio de las mismas. Una regla sencilla es utilizar solo la raíz cuadrada del número total de variables predictoras en cada nodo.
Por ejemplo, si tenemos un conjunto de datos con 16 variables predictoras, en cada nodo de cada árbol se consideran solo 4, elegidas al azar, para ver cuál es la mejor candidata para decidir ese nodo. Esto hace que ya no se usen de forma obligada las que tienen más capacidad predictiva y se da oportunidad a las que tienen menos. Como resultado, los árboles se parecen menos y paliamos el problema de la autocorrelación.
Podemos hacer un random forest con R y compararlo con el que hicimos antes con bagging. En este caso la varianza explicada es prácticamente la misma, un 84,6%, aunque lo más habitual es que mejore un poco respecto a la obtenida con bagging. Podéis ver el análisis con R en este enlace.
También puede cambiar algo la importancia de las variables, ya que algunas que podrían no ser seleccionadas en el contexto de bagging debido a su menor importancia relativa podrían terminar siendo más influyentes en algunos árboles. Además, al reducir la correlación entre los árboles, las variables que estaban correlacionadas con otras en el modelo de bagging pueden mostrar una importancia diferente en un random forest.
En cualquier caso, la reducción de la correlación entre los árboles consigue que el modelo capture mejor la varianza total de los datos, mejorando así su capacidad de hacer predicciones con datos nuevos.
Potenciando el rendimiento de los árboles
Volvemos a encontrarnos con una palabra en inglés consagrada por su éxito de utilización: el boosting.
Al igual que el bagging, el boosting son un conjunto de técnicas que se emplean en regresión y en clasificación para potenciar el rendimiento de los modelos. En el caso de los árboles, mientras que en el bagging y en los random forest los árboles se entrenan de forma independiente y se promedian, en el boosting los modelos se entrenan secuencialmente y cada nuevo árbol se construye para corregir los errores de los árboles anteriores.
La idea, explicada de forma muy sencilla, es la siguiente. Se comienza con un árbol muy simple, con poca profundidad de nodos. A partir de ahí, se van entrenando los nuevos árboles de forma secuencial para corregir los errores residuales de los anteriores, intentando mejorar sus predicciones, ajustando la importancia de las variables y el peso relativo de cada observación. Finalmente, se combinan todos los árboles generados para hacer la predicción final, sumando las predicciones ponderadas de todos los árboles (en regresión) o por votación ponderada (en clasificación).
De los tres que hemos visto, este tipo de abordaje es el que tiene más capacidad para reducir tanto el sesgo como la varianza respecto a los árboles de decisión simples.
Con estos algoritmos entramos de lleno en el mundo del aprendizaje automático, donde existen distintos tipos de algoritmos de boosting, desde el boosting adaptativo (AdaBoost) o el boosting con gradiente (gradient boosting), hasta los algoritmos más avanzados como XGBoost, LightGBM y CatBoost.
Digamos únicamente que XGBoost es particularmente popular por su eficiencia y precisión, y permite el uso de técnicas de regularización para evitar el sobreajuste. LightGBM y CatBoost son alternativas que están diseñadas para mejorar el tiempo de ejecución y manejar mejor conjuntos de datos con características específicas (como categóricas). En cualquier caso, nos adentramos en unas aguas cuya profundidad no vamos a explorar en esta entrada.
Nos vamos…
Y aquí vamos a dejar los árboles por hoy.
Hemos visto cómo las técnicas de bagging (agregación por remuestreo) permiten mejorar las limitaciones de los árboles de decisión simples y cómo podemos ir algunos pasos más allá para ir afinando el modelo en esa lucha interminable entre sesgo y varianza.
El objetivo es siempre el mismo: conseguir predicciones precisas, pero evitando el sobreajuste para que el modelo funcione también con datos nuevos, no solo con los de entrenamiento que utilizamos para construirlo.
De todas formas, no penséis que hemos hablado de todos los árboles que podemos elaborar o utilizar. Para los amantes de las emociones fuertes, tenemos también los árboles de regresión aditiva bayesiana.
Estos utilizan un enfoque de modelado estadístico no paramétrico que combina técnicas de árboles de decisión con principios bayesianos. Estos modelos tienen una gran capacidad para manejar relaciones complejas y no lineales entre las variables, así como para proporcionar inferencias probabilísticas sobre las predicciones. Pero esa es otra historia…
