Elección de la prueba estadística.

Se describe la prueba estadística más idónea según el tipo de variable, si se trata o no de datos pareados y de si siguen una distribución normal. Los casos más habituales serán los de comparación de medias, comparación de proporciones y cálculos de coeficientes de correlación entre dos variables.
Todos conoceréis el caso de alguien que, tras realizar un estudio y recoger varios millones de variables, se ha dirigido al estadístico de su centro de trabajo y, demostrando de forma fehaciente su claridad de ideas respecto a su trabajo, le ha dicho: por favor (hay que ser educados), crúzalo todo con todo, a ver qué sale.
Llegados a este punto te pueden ocurrir varias cosas. Si el estadístico es un desalmado sin escrúpulos te dirigirá una media sonrisa y te dirá que vuelvas al cabo de unos días. Entonces te dará varios centenares de hojas con gráficos, tablas y números que no sabrás por dónde coger. Otra cosa que te puede ocurrir es que te mande a paseo, cansado como estará de que le hagan peticiones semejantes.
Pero puedes tener suerte y encontrar un estadístico competente y paciente que, de forma abnegada, te explicará que la cosa no debe funcionar así. Lo lógico es que tú, antes de recoger ningún dato, hayas elaborado una memoria del proyecto en la que esté previsto, entre otras cosas, qué hay que analizar y qué variables hay que cruzar entre sí. Incluso, te puede sugerir que, si el análisis no es muy complicado, intentes hacerlo tú mismo.
Esto último te puede parecer el desvarío de una mente trastornada por las matemáticas pero, si lo piensas un momento, no es tan mala idea. Si nosotros hacemos el análisis, al menos el preliminar, de nuestros resultados, nos puede ayudar a entender mejor el estudio. Además, ¿quién mejor que nosotros mismos puede saber lo que queremos?
Con los paquetes estadísticos actuales, la estadística bivariante más sencilla puede estar a nuestro alcance. Únicamente tenemos que tener buen cuidado en saber elegir el test de contraste de hipótesis adecuado, para lo cual habremos de tener en cuenta tres aspectos: el tipo de variables que queremos comparar, si los datos son apareados o independientes y si tenemos que utilizar test paramétricos o no paramétricos. Veamos estos tres aspectos.
Elección del método estadístico
En cuanto al tipo de variables, existen múltiples denominaciones según la clasificación o el paquete estadístico que utilicemos pero, simplificando, diremos que hay tres tipos de variables. En primer lugar, están las continuas o de escala. Como su nombre indica, recogen el valor de una variable continua como puede ser el peso, la talla, la glucemia, etc. En segundo lugar, están las variables nominales, que constan de dos o más categorías que son mutuamente excluyentes. Por ejemplo, la variable color de pelo puede tener las categorías “moreno”, “rubio” y “pelirrojo”.
Cuando estas variables tienen dos categorías, las llamamos dicotómicas (sí/no, vivo/muerto, etc.). Por último, cuando las categorías están ordenadas por rango, hablamos de variables ordinales: “no fuma”, “fuma poco”, “fuma moderadamente”, “fuma mucho”. Aunque a veces puedan usar números, estos indican la posición de las categorías dentro de la serie, sin implicar, por ejemplo, que la distancia de la categoría 1 a la 2 sea la misma que la de la 2 a la 3. Por ejemplo, podemos clasificar el reflujo vesicoureteral en grados I, II, III y IV (tener un grado IV es más que un II, pero no significa que se tenga el doble de reflujo).
El tipo de variable
Saber qué tipo de variable tenemos entre manos es sencillo. Si tenemos duda, podemos seguir el siguiente razonamiento basado en la respuesta a dos preguntas:
- ¿Tiene la variable valores teóricos infinitos? Aquí hay que abstraerse un poco y fijarse en los de “valores teóricos”. Por ejemplo, si recogemos el peso de nuestros participantes, los valores teóricos serán infinitos aunque, en la práctica, esto estará limitado por la precisión de nuestra báscula. Si la respuesta es sí estaremos antes una variable continua o de escala. Si es no, pasamos a la siguiente pregunta.
- ¿Los valores están ordenados en algún tipo de rango? Si la respuesta es sí, nos encontraremos ante una variable ordinal. Si la respuesta es no, tendremos una variable nominal.
Medidas apareadas o independientes
El segundo aspecto es el de las medidas apareadas o independientes. Dos medidas están apareadas cuando se mide una variable en dos ocasiones tras haber aplicado algún cambio, habitualmente en el mismo sujeto. Por ejemplo: presión arterial antes y después de un test de esfuerzo, peso antes y después de una intervención nutricional, etc. Por su parte, las medidas independientes son aquellas que no tienen relación entre sí (son variables diferentes): peso, talla, género, edad, etc.
Paramétrico vs no paramétrico
Por último, hemos mencionado lo de poder utilizar test paramétricos o no paramétricos. No vamos a entrar ahora en detalle, pero para poder utilizar un test paramétrico la variable debe cumplir una serie de características, como seguir una distribución normal, tener un determinado tamaño muestral, etc. Además, hay técnicas que son más exigentes que otras a la hora de tener que cumplir estas condiciones. Ante la duda, es preferible utilizar técnicas no paramétricas sin necesidad (el único problema es que es más difícil conseguir significación estadística, pero el contraste es igual de válido) que usar una prueba paramétrica cuando no se cumplan los requisitos necesarios.
Una vez que ya hemos dado respuesta a estos tres aspectos, solo nos queda hacer las parejas de variables que vamos a comparar y elegir el test estadístico apropiado. Lo podéis ver resumido en la tabla adjunta.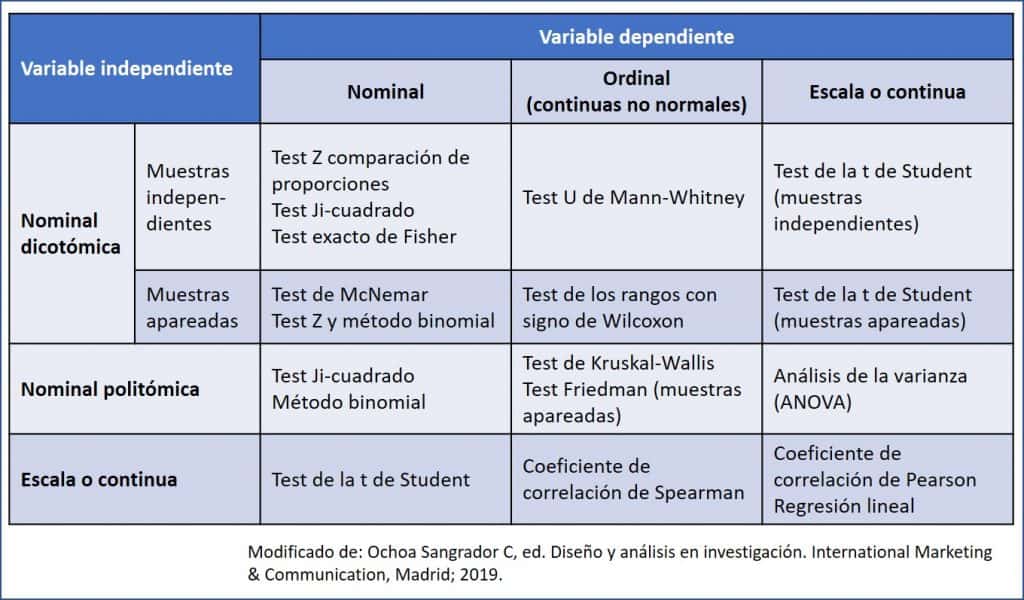
De todas formas, no os lieis: el programa estadístico hará el contraste de hipótesis sin tener en cuenta cuál es la dependiente y cuál la independiente, solo tendrá en cuenta los tipos de variables.
La tabla se explica sola, así que no le vamos a dar muchas vueltas. Por ejemplo, si hemos medido la presión arterial (variable de escala) y queremos saber si hay diferencias entre hombres y mujeres (género, variable nominal dicotómica), el test adecuado será el de la t de Student para muestras independientes. Si quisiéramos ver si hay diferencia en la presión antes y después de un tratamiento, utilizaríamos el mismo test de la t de Student pero para muestras apareadas.
Otro ejemplo: si queremos saber si hay diferencias significativas en el color de pelo (nominal politómica: “rubio”, “moreno” y “pelirrojo) y si el participante es del norte o sur de Europa (nominal dicotómica), podríamos emplear un test de la Ji-cuadrado.
Nos vamos…
Y aquí lo vamos a dejar por hoy. No hemos hablado nada de las peculiaridades de cada test que debemos tener en cuenta, sino que solo hemos mencionado el test en sí. Por ejemplo, la ji-cuadrado tiene que cumplir unos mínimos en cada casilla de la tabla de contingencia, en el caso de la t de Student debemos considerar si las varianzas son iguales (homocedasticidad) o no, etc. Pero esa es otra historia…
