Cramer’s V.

Travelling is one of my favourite hobbies. I love seeing new places and learning about people’s customs in different countries around the world. It’s hard to believe that the same human being has such different habits in different places.

To illustrate what I’m telling you, we can look at data on people’s favourite hobbies and favourite drinks in two countries: Italy and South Korea. During my travels in those places, I asked around and discovered that, although the questions were the same (favourite activity between cooking, sports, reading, or hanging out with friends, and favourite drink between coffee, wine, or mineral water), the answers seemed to follow different patterns in each country.

In Italy, I noticed something curious: coffee lovers tend to prefer reading, while those who choose wine enjoy hanging out with friends more. Here there seems to be a synchronicity in tastes, as if the combinations between drink and activity were more than just coincidences. However, in South Korea, the choices are more scattered and there doesn’t seem to be a clear link between what someone drinks and their hobby. Coffee fans can enjoy cooking as much as they enjoy exercising, without any clear pattern.

So how do we put numbers to this apparent Italian harmony versus Korean chaos? Sure, the chi-square test will tell us if there is any association between drink and activity in each country, but that only gives us a “yes” or a “no.” What if we want to know how much stronger that connection is in Italy than in South Korea? This is where we need something with more spark: Cramer’s V.

This tool not only detects whether variables are associated, but allows us to measure how intense that relationship is in each group, almost like putting a cultural thermometer. Thus, we can compare the intensity of the connections between tastes in two different worlds and discover how much of these choices respond to patterns or is just a matter of chance. It’s time to quantify the unquantifiable!

Cramer’s V

When we think about measuring the strength of the association between variables, it is common for our minds to go straight to the use of coefficients such as Pearson’s correlation coefficient or Spearman’s coefficient. These tools are perfect for quantitative variables (Pearson’s coefficient), where we can draw scatter graphs and calculate linear trends, as well as for ordinal variables (Spearman’s coefficient). But what happens if our variables are not continuous numbers, but nominal categories with no order relationship between them?

For this scenario, statistics offers us a hero who is a little less known, but equally talented: Cramer’s V. This measure is ideal for evaluating the association between two nominal variables, such as favorite activity and preferred drink, giving us a number between 0 (no association) and 1 (perfect association).

Some of you may be wondering why there is any need to complicate your life with Cramer’s V when we can resort to other, more well-known measures of association, such as risk ratio. The reason is that Cramer’s V offers us a simpler and more elegant interpretation when the variables we have to compare have more than two categories.

Let’s think about it for a moment. In the classic context of a 2×2 table, the risk ratio measures the ratio between the probabilities of the event occurring in the groups exposed to a certain factor and those not exposed. This is simple and straightforward.

However, when the variables have multiple categories, although we can extend the calculation of risks ratios, we will no longer have a single figure, but several risks ratios to interpret, since we will have to evaluate the specific comparisons for each combination of categories, which makes it difficult to summarize the relationship in a single value. It is in these situations where Cramer’s V shines with its own light, since it condenses the relationship in a single figure.

Of course, let’s remember that the variables to be compared must be categorical and not ordinal.

About Italians and Koreans

Let’s go back to my travel memories to illustrate how Cramer’s V works.

First let’s take a look at the contingency tables, which I show you in the following figure. I have colored the cells of the tables with a more intense color as the frequency of each table increases. In this way, we can see at a glance which are the most popular cells and, consequently, the categories of the two variables that tend to be most associated.

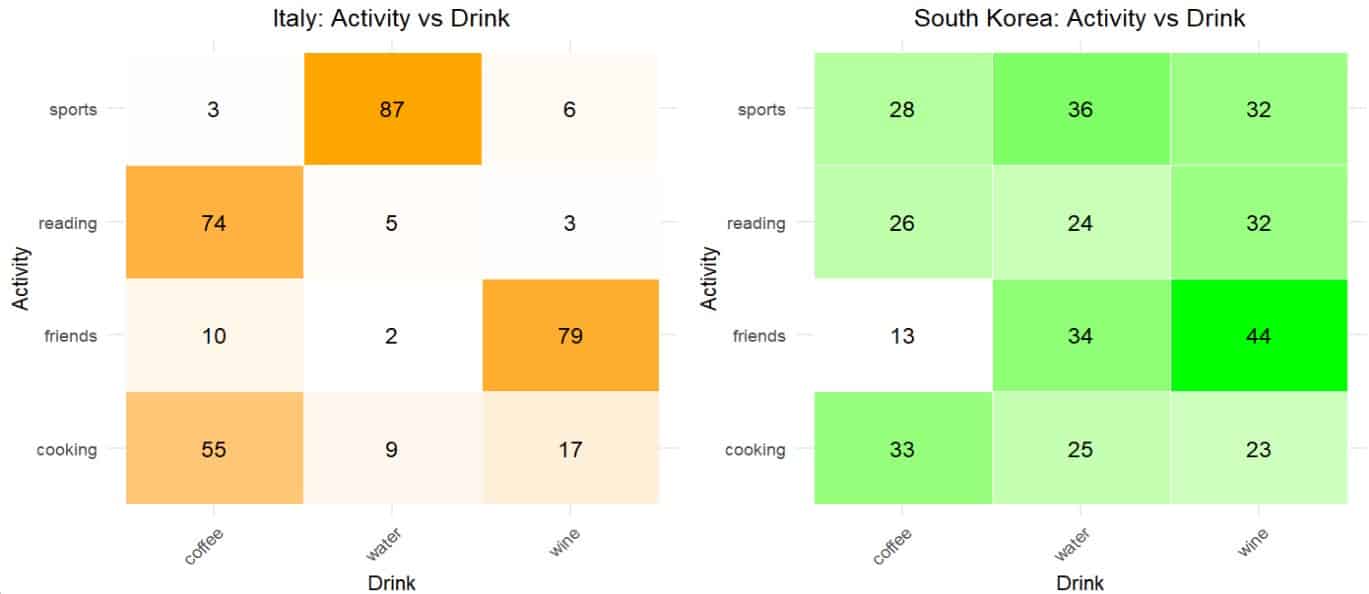
Let’s first look at the table of the Italians. We see that there are striking differences in the intensity of the colors, which already warns us that some associations are more frequent than others.

We see, for example, that those who prefer to go out with friends are more fond of wine. On the other hand, sports fans are more in favor of drinking water. This does not surprise me in the least: bad habits are often associated. To finish the Italian analysis, we see that readers and cooks tend to prefer coffee.

If we look at the Korean table, we see that these differences are not so clear. The colours of the cells are much more uniform, although there seem to be habits that are more closely associated, such as sport and water or how little people like coffee and prefer to go out partying with friends.

This analysis is all very well for home use, but you already know that I like to quantify things. Let’s see if we can measure the strength of the association of these combinations of habits that seem to exist when we look at numbers and colours.

Cramer’s V again

Cramer’s V is quite simple to calculate. We have to divide the chi-square statistic by the product of the sample size and the minimum number of degrees of freedom between rows and columns. Finally, we take the square root of the result of all this.

Let’s start with the Italians. The first thing is to calculate the value of the chi-square statistic for a test of independence. I’ll spare you the formula, which you have in a previous post. I have calculated it with the R program and I get a value of 424.2, with 6 degrees of freedom and a p value of almost 0, statistically significant.

So we already know that there is a significant association between the two nominal variables, the favorite activity and the preferred drink. To quantify the strength of this association, we calculate Cramer’s V. We already know the value of the chi-square statistic (424.4) and we can count the frequencies in the table to obtain the sample size (350). Since it is a 4×3 table, the minimum number of degrees of freedom for rows and columns will be 3 – 1 = 2. We do the math and we get a V = 0.78.

We already know that Cramer’s V can have values ​​between 0 and 1. In general, values ​​less than 0.1 indicate that there is no association, between 0.1-0.3 the strength of the association is small, between 0.3-0.5 the effect is said to be moderate and finally, when V is greater than 0.5, the variables are said to be strongly associated.

We have already quantified the association in the Italians. The result confirms the impression we had when looking at the contingency table: the two variables show a strong association. Let’s now see if the Koreans are as chaotic as we thought when examining their table.

We first calculate the value of the chi-square statistic, which turns out to be 17.56, with 6 degrees of freedom and a p value = 0.007. It turns out that there is no such chaos, since we do see that the two variables are associated in a statistically significant way.

However, we assume that Cramer’s V will have a much lower value than that of the Italians. Indeed, if we do the calculations we see that it is 0.16, so we conclude that the strength of association of these two variables in South Korea is very low.

We’re leaving…

And we have come this far.

I would not like to finish without warning the public that the data we have used in the post are totally fictitious. May the Italians and South Koreans forgive me if any of them feel offended by the assignment of a favorite activity or drink.

In any case, we have seen how to assess whether two nominal categorical variables are associated in an almost choreographed way or if, on the contrary, they present a more chaotic mosaic, showing how numbers, which also have their cultural flavor, allow us to quantify the association in an almost surgical way.

This example makes me wonder if association and chance can also be explored in other areas of life, such as the choice of a partner or the success of a film. After all, the magic of probability is everywhere. There are other techniques that we have not mentioned in this post, such as Poisson regression, which can help us predict unexpected phenomena or decode spurious correlations. But that is another story…