Entrenamiento de los algoritmos de aprendizaje automático.

¿Te gustaría ser el cuarto mosquetero (o la cuarta, para el caso)? Ya sabes, unirte a la pandilla de los tres legendarios: Atos, Portos y Aramis. ¿Cuál sería tu función? ¿Serías el que corre a avisar al resto cuando las cosas se ponen feas, el que cuenta los golpes recibidos, o tal vez el que siempre tiene un plan B en la manga? Pues bien, en el mundo del entrenamiento de los algoritmos de aprendizaje automático, también hay tres mosqueteros fundamentales: la función de pérdida, la métrica de desempeño y el control de validación. Y, sí, cada uno tiene su papel esencial en esta épica batalla de datos.

La función de pérdida es como Atos, el pensador melancólico que sabe cuánto duele cada error. Ella se encarga de medir las heridas de nuestro algoritmo y nos dice cuánto nos hemos desviado del objetivo. La métrica de desempeño, por otro lado, se parece más a Portos, el fanfarrón que siempre está sacando cuentas y mostrando cuán bien (o mal) estamos haciendo las cosas. Finalmente, el control de validación es el Aramis del grupo: reflexivo, meticuloso, siempre asegurándose de que estamos en el camino correcto, evitando que nos emocionemos demasiado cuando las victorias vienen demasiado fáciles.

Así que, cuando entrenamos un algoritmo, no estamos muy lejos de aquellas aventuras de capa y espada. Tres componentes, tres papeles esenciales, cada uno con su espada (o fórmula matemática) lista para enfrentarse al próximo desafío. Ahora, solo queda decidir si eres D’Artagnan o Richelieu en esta historia… ¿Listo para la esgrima estadística? ¡En guardia!

Las vueltas de la vida… de un algoritmo

En el aprendizaje automático, las cosas se hacen de forma diferente a como estábamos acostumbrados con la estadística de toda la vida. Su elemento central es el algoritmo, que podemos definir como una secuencia finita y ordenada de pasos o instrucciones que se siguen para resolver un problema o realizar una tarea.

Pensemos en el ejemplo más sencillo que se me ocurre ahora mismo: la regresión lineal simple.

A alguien se le debió ocurrir que lo mejor sería encontrar los parámetros de la recta de regresión (el intercepto y la pendiente) que se aproximase mejor a todos los puntos de la nube que producían las observaciones, los datos disponibles. Esto dio lugar al método de los mínimos cuadrados, que ya vimos en una entrada anterior.

En este método se plantean las reglas que debe cumplir el modelo de regresión y se resuelven algebraicamente para calcular los valores de los parámetros. Como es lógico, estos valores dependerán de los datos que utilicemos, pero el método de calcular el intercepto y la pendiente es siempre el mismo. De una manera simplista, podemos decir que al método de los mínimos cuadrados le da igual qué datos le demos: siempre calculará los parámetros con las mismas fórmulas.

Sin embargo, en el aprendizaje automático las cosas funcionan de otra manera. Aquí, un algoritmo empieza a dar vueltas y a probar valores diferentes para los parámetros, hasta que aprende de los datos cuáles son los valores óptimos que permiten un mejor ajuste del modelo. Esta es la diferencia fundamental: mientras que el método de los mínimos cuadrados utiliza unas normas fijas y predefinidas para calcular los parámetros, el algoritmo de aprendizaje automático da vueltas y más vueltas para aprenderlos de los datos que le damos, hasta que los encuentra.

A estas vueltas es a lo que llamamos el entrenamiento del algoritmo. Empieza con unos valores de los parámetros que suelen ser aleatorios y, vuelta tras vuelta, los va ajustando hasta encontrar los óptimos. ¿Cómo lo hace? Pues con la ayuda de nuestros tres mosqueteros.

Veámoslo.

Aprendiendo de los datos

En la figura adjunta podéis ver un esquema de las vueltas de la vida de un algoritmo durante su entrenamiento.

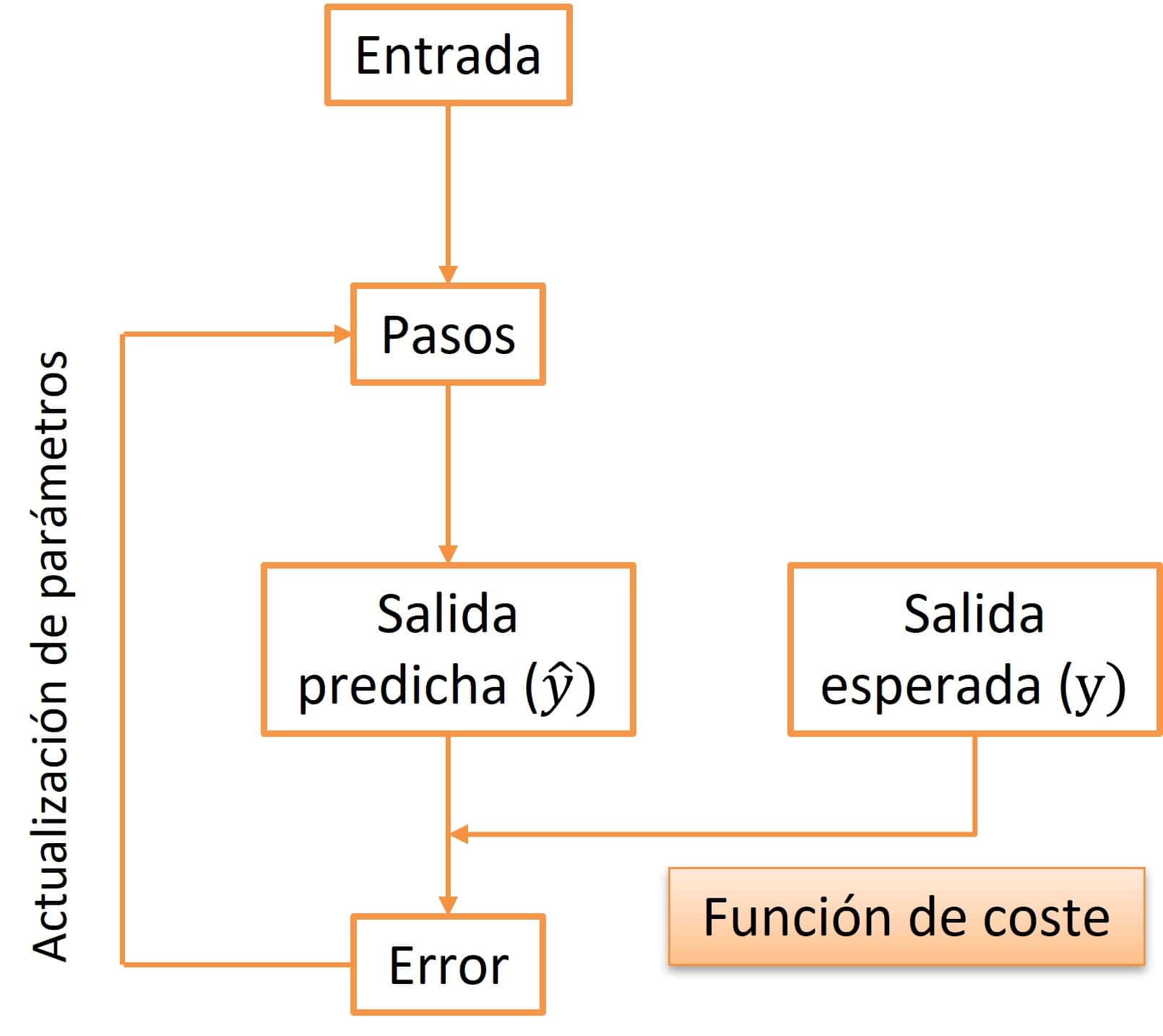
Siguiendo con nuestro ejemplo de la regresión lineal simple, disponemos de un conjunto de datos con dos variables, “x” e “y”. Lo que buscamos es un modelo que sepa predecir el valor de “y” que se asociará a un nuevo valor de “x” que nos encontremos por ahí. Tendremos que buscar los valores de los parámetros “a” y “b” de la siguiente recta:

y = a + bx

Usando nuestros datos, que llamamos de entrenamiento, empezamos por utilizar los de la variable «x» como entrada al algoritmo. En el primer ciclo, se establecen unos valores de «a» y «b», generalmente al azar y se multiplica «x» por el valor de «b» y se le suma el valor de «a». Con esto obtenemos una predicción de «y».

A continuación, comparamos el valor de esta predicción con el valor real de los datos de entrenamiento. Como hemos elegido los valores de los parámetros al azar, lo lógico es que el valor predicho y el real se parezcan poco en esta primera vuelta. De esta comparación se encarga la función de coste o de pérdida.

El objetivo fundamental de la función de coste es minimizar la diferencia entre estos dos valores, el predicho y el real o, lo que es lo mismo, minimizar los errores de predicción del futuro modelo que se obtendrá tras el entrenamiento. Para ello, sirve de guía a otro algoritmo, el algoritmo de optimización, que es el que se encarga de modificar un poco los parámetros «a» y «b» para que el error sea menor.

Una vez modificados los parámetros, el ciclo se repite, optimizando un poco más los parámetros en cada vuelta y disminuyendo el error de predicción, hasta que se alcanzan los valores de los parámetros con los que se obtiene un error tan bajo como se desee.

De forma paralela, podemos ir viendo cómo se desempeña el modelo para realizar la predicción de datos nuevos en cada vuelta. Una vez que hemos pasado todos los valores de «x» por el algoritmo con unos determinados valores de los parámetros, utilizamos nuestro segundo mosquetero para ver qué tal lo hace. En el caso de la regresión lineal podemos medir el error cuadrático medio, su raíz cuadrada, el coeficiente de determinación (R²), o cualquier otra medida de desempeño en las que no vamos a profundizar en esta entrada.

¿Y cuántas vueltas tiene que dar el algoritmo? Pues depende de los datos y del error que estemos dispuestos a tolerar. Uno podría pensar que cuantas más vueltas dé, mejor será el ajuste. Pero si lo hacemos así, aparecerá en escena el Richelieu de nuestra historia, que no es otro que el sobreajuste, también conocido por su alias en inglés: overfitting.

Para evitar esto, no tenemos más remedio que recurrir a otro de nuestros tres mosqueteros: el control de la validación durante la fase del entrenamiento.

La sabiduría de parar a tiempo

Ya hemos visto cómo el algoritmo va, poco a poco, aprendiendo de los datos de entrenamiento para optimizar cada vez más los parámetros de la recta que estamos buscando.

El problema es que el algoritmo, al comienzo, aprende de los datos, pero, llegado un determinado momento, si sigue dando vueltas ya no aprende de ellos, sino que comienza a aprendérselos de memoria, por decirlo de una forma fácil de comprender.

Cuando el algoritmo está aprendiendo, el error va disminuyendo con cada vuelta, al acercarse los parámetros cada vez más a su valor óptimo. De forma parecida, la función de desempeño nos va indicando mejores resultados después de cada ciclo.

Si damos el número de vueltas suficiente, el error se aproximará a cero y la función de desempeño a su valor máximo, indicando un ajuste perfecto del modelo. Pero esto es un espejismo traicionero, ya que el ajuste perfecto se habrá obtenido con los datos de entrenamiento, pero el modelo fracasará estrepitosamente cuando intente hacer nuevas predicciones con datos que no haya visto durante esta fase.

Esto es el sobreajuste: el modelo empieza aprendiendo la relación entre los datos, pero llega un momento en que lo que aprende es el ruido aleatorio que va implícito en el conjunto de datos de entrenamiento. Esto es a lo que nos referimos al decir que se ha aprendido los datos de memoria.

Imaginad un estudiante que se aprende un problema de física de memoria, sin preocuparse de entender cuáles son las leyes que permiten resolverlo. Si en el examen le ponen el mismo problema, aprobará con la mejor nota, pero si le ponen un problema ligeramente diferente, suspenderá clamorosamente, aunque el razonamiento para resolver el problema sea el mismo que el del problema que estudió.

Para evitar que al algoritmo que estemos entrenando le pase igual que a nuestro estudiante, en cada vuelta introducimos, como entrada, además del dato de entrenamiento, un datos de otro conjunto que llamamos de validación.

Así, tenemos dos entradas (entrenamiento y validación) y sus correspondientes salidas, que son evaluadas por la función de coste y la de desempeño, después de cada vuelta.

Cuando el algoritmo está aprendiendo de los datos, la función de coste disminuirá con los dos conjunto de datos, mientras que la de desempeño mejorará también en ambos.

En el momento en que el algoritmo comience a memorizar los datos, veremos que con los datos de validación dejan de mejorar las dos o, incluso, empeoran. El error de la función de coste deja de disminuir o, incluso, aumenta, mientras que al desempeño le ocurre lo contrario: deja de mejorar o, incluso, disminuye. El modelo comienza a degradarse.

Este es el momento de parar el entrenamiento o, incluso, mejor, un poco antes. Así conseguiremos un modelo que quizás no haga un ajuste tan bueno de los datos de entrenamiento, pero que tendrá una mejor capacidad de generalizarse y de realizar predicciones con datos nuevos.

Pensad que los modelo se hacen para hacer predicciones con datos de los que no conocemos su resultado. Los de los datos de entrenamiento ya los sabemos, no nos hace falta ningún modelo que nos los calcule.

Nos vamos…

Y creo que con esto hemos llegado al final de este emocionante recorrido en compañía de nuestros mosqueteros: la función de coste, la métrica de desempeño y el control de validación del entrenamiento de un algoritmo.

Hemos visto que, al igual que en las aventuras de D’Artagnan, el éxito en esta travesía no depende solo de la habilidad individual de cada mosquetero, sino de su coordinación y equilibrio. En el entrenamiento de algoritmos, evitar el sobreajuste es como esquivar las intrigas de Richelieu: se necesita un ojo atento y un plan estratégico. Porque, al final, el verdadero objetivo no es ganar cada duelo, sino estar listos para cualquier batalla futura, prediciendo con precisión.

Por cierto, no hemos hablado nada del D’Artagnan de esta historia, al que hemos mencionado muy de paso. Me refiero al algoritmo de optimización, que es el que se encarga de ir ajustando los parámetros bajo la guía de la función de coste, generalmente utilizando alguna variación del método del descenso por gradiente. Pero esa es otra historia…