Representación de variables cualitativas.

Se describen dos de los gráficos más utilizados para variables cualitativas: el de sectores y el de barras. Se hace mención también al gráfico de Pareto.
Cuando uno lee el título de esta entrada puede preguntarse con qué estúpida ocurrencia voy a machacar hoy a la sufrida concurrencia, pero no temáis, lo único que vamos a hacer es poner en valor ese famoso aforismo que dice que una imagen vale más que mil palabras. ¿Os he aclarado algo? Supongo que no.
Como todos sabemos, la estadística descriptiva es aquella rama de la estadística que utilizamos habitualmente para obtener una primera aproximación a los resultados de nuestro estudio, una vez que lo hemos terminado.
Lo primero que hacemos es describir los datos, para lo cual realizamos tablas de frecuencias y utilizamos medidas diversas de centralización y dispersión. El problema con estos parámetros es que, aunque representan verdaderamente la esencia de los datos, a veces es difícil proporcionar con ellos una visión sintética y comprensiva.
Es en estos casos en los que podemos recurrir a otro recurso, que no es otro que la representación gráfica de los resultados del estudio. Ya sabéis, una imagen vale más que mil palabras, o eso dicen.
Hay multitud de tipos de gráficos para ayudarnos a comprender mejor la representación de los datos, pero hoy nos vamos a limitar a aquellos que tienen que ver con las variables cualitativas o categóricas.
Recordad que las variables cualitativas representan atributos o categorías de la variable. Cuando la variable no incluye ningún sentido de orden, se dice que es cualitativa nominal, mientras que si se puede establecer cierto orden entre las categorías diríamos que es cualitativa ordinal. Por ejemplo, la variable “fumador” sería cualitativa nominal si tiene dos posibilidades: “sí” o “no”. Sin embargo, si la definimos como “ocasional”, “poco fumador”, “moderado” o “muy fumador”, ya existe cierta jerarquía y hablamos de variable cualitativa ordinal.
Representación de variables cualitativas
El primer tipo de gráfico que vamos a considerar a la hora de representar una variable cualitativa es el gráfico de sectores, mucho más conocido como gráfico de tarta. Este consiste en una circunferencia cuya área representa el total de los datos. Así, a cada categoría se le asigna un área que será directamente proporcional a su frecuencia. De esta forma, las categorías más frecuentes tendrán áreas mayores, de modo que de un vistazo podemos hacernos una idea de cómo se distribuyen las frecuencias en las categorías.
Diagrama de sectores
Hay tres formas de calcular el área de cada sector. La más sencilla es multiplicar la frecuencia relativa de cada categoría por 360°, obteniendo los grados de ese sector.
La segunda es utilizar la frecuencia absoluta de la categoría, según la siguiente regla de tres:
Frecuencia absoluta / Frecuencia total de datos = Grados del sector / 360°
Por último, la tercera forma consiste en utilizar las proporciones o porcentajes de las categorías:
% de la categoría / 100% = Grados del sector / 360°
Las fórmulas son muy sencillas, pero, de todas formas, no habrá necesidad de recurrir a ellas porque el programa con el que hagamos el gráfico lo hará por nosotros. La instrucción en R es pie(), tal como podéis ver en la primera figura, en la que os muestro una distribución de niños con enfermedades exantemáticas y cómo se representaría el gráfico de sectores.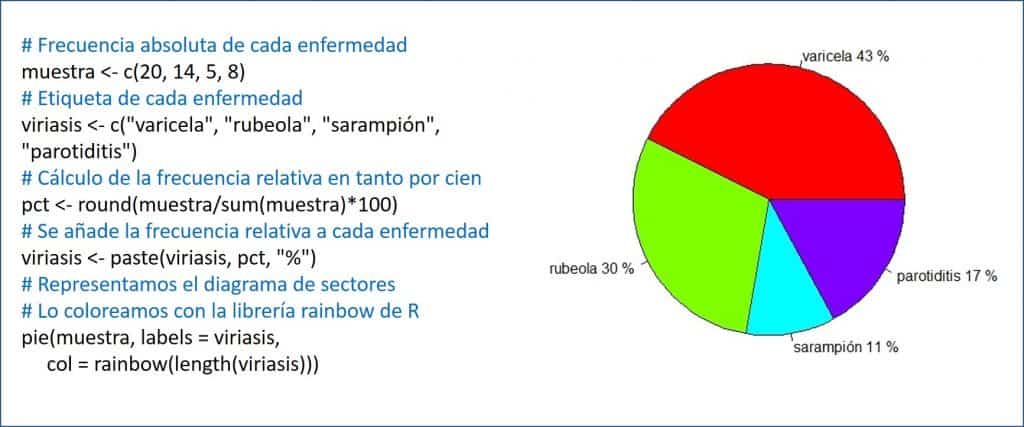
Por ejemplo, si hacemos un gráfico de sectores para una variable cualitativa ordinal estaremos perdiendo la información sobre la jerarquía de las variables, por lo que resultaría más correcto utilizar un gráfico que permita ordenar las categorías de menos a más. Y este gráfico no es otro que el diagrama de barras, del que hablaremos a continuación.
El diagrama de sectores será especialmente útil cuando haya pocas categorías de la variable. Si hay muchas, la interpretación deja de ser tan intuitiva, aunque siempre podemos completar el gráfico con una tabla de frecuencias que nos ayude a interpretar mejor los datos. Otro consejo es tener mucho cuidado con los efectos en 3D a la hora de dibujar las tartas. Si nos pasamos de elaborados, el gráfico perderá claridad y será más difícil de leer.
Diagrama de barras
El segundo gráfico que vamos a ver es, ya lo hemos mencionado, el gráfico de barras, el óptimo para representar las variables cualitativas ordinales. En el eje horizontal se representan las diferentes categorías y sobre él se levantan unas columnas o barras cuya altura es proporcional a la frecuencia de cada categoría. También podríamos utilizar este tipo de gráfico para representar variables cuantitativas discretas, pero lo que no es muy correcto hacer es usarlo para las variables cualitativas nominales.
El diagrama de barras es capaz de expresar la magnitud de las diferencias entre las categorías de la variable, pero ahí está, precisamente, su punto débil, ya que es fácilmente manipulable si modificamos las escalas de los ejes. Por eso hay que tener cuidado al analizar este tipo de gráficos para evitar que nos engañen con el mensaje que el autor del estudio pueda querer transmitir.
Este gráfico también es sencillo de hacer con la mayor parte de los programas estadísticos y hojas de cálculo. La función en R es barplot(), como veis en la segunda figura, que representa la gravedad de una muestra de niños asmáticos.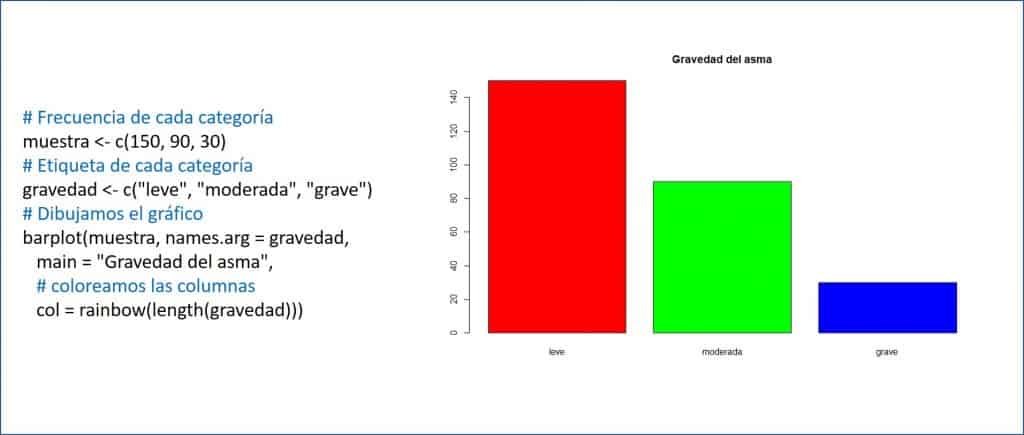
Diagrama de Pareto
Pareto fue un italiano que nació a mediados del siglo XIX en París. Esta pequeña contradicción se debe a que su padre estaba entonces exiliado en Francia por ser uno de los seguidores de Giuseppe Mazzini, que estaba entonces empeñado en la unificación italiana.
De todas formas, Pareto vivió en Italia desde los 10 años de edad, convirtiéndose en un ingeniero con amplios conocimientos matemáticos y humanistas y que contribuyó de manera decisiva al desarrollo de la microeconomía. Hablaba y escribía con fluidez en francés, inglés, italiano, latín y griego, y se hizo famoso por multitud de contribuciones como la distribución de Pareto, la eficiencia de Pareto, el índice de Pareto y el principio de Pareto. Para representar este último inventó el diagrama de Pareto, que es el que le trae hoy aquí entre nosotros.

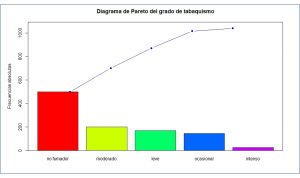
Como es fácil de comprender, esta priorización hace que el diagrama de Pareto sea especialmente útil para representar variables cualitativas ordinales, superando al diagrama de barras al dar información sobre el porcentaje acumulado al ir agregando las categorías de la distribución de la variable.
El cambio de pendiente de esta curva nos informa también del cambio en la concentración de datos, que depende de la variabilidad en que los sujetos de la muestra se reparten entre las distintas categorías.
Por desgracia, R no dispone de una función simple para representar diagramas de Pareto, pero podemos obtenerlo fácilmente con el script que os adjunto en la tercera figura, obteniendo el gráfico de la cuarta.
Nos vamos…
Y aquí lo vamos a dejar por hoy. Antes de decir adiós quiero avisaros que no debéis confundir las barras del diagrama de barras con las del histograma ya que, aunque pueden parecerse desde el punto de vista gráfico, ambos representan cosas muy diferentes. En un diagrama de barras solo se representan los valores de las variables que hemos observado al hacer el estudio.
Sin embargo, el histograma va mucho más allá ya que, en realidad, encierra la distribución de frecuencias de la variable, por lo que representa todos los valores posibles que existen dentro de los intervalos, aunque no hayamos observado ninguno de forma directa. Permite así calcular la probabilidad de que se represente cualquier valor de la distribución, lo que es de gran importancia si queremos hacer inferencia y estimar valores de la población a partir de los resultados de nuestra muestra. Pero esa es otra historia…
