La maldición de la multidimensionalidad.

Me pregunto cómo podría atravesar un bosque lleno de senderos, cada uno con carteles que prometen llevarme al lugar perfecto: la cabaña en la montaña, la playa secreta, o ese claro donde la luz del sol siempre brilla. Fascinado, podría decidir tomar todos los caminos a la vez, haciendo malabares entre direcciones opuestas.

¿El resultado? Me quedaría dando vueltas, atrapado entre posibilidades, sin llegar a ninguna parte. ¿Os suena frustrante? Pues esto mismo ocurre cuando los modelos estadísticos intentan abarcar demasiadas variables a la vez.

En estadística, este fenómeno se conoce como la maldición de la dimensionalidad. Cuando hay casi tantos, o incluso más, caminos (variables) que lugares a los que ir (observaciones), las técnicas clásicas como la regresión quedan atrapadas. El modelo se ajusta tanto a los datos disponibles que parece perfecto, pero en realidad ha perdido completamente el rumbo: no puede predecir nada útil más allá del bosque donde fue creado. Es como si esos senderos solo existieran en un mapa dibujado a mano por un cartógrafo con demasiada imaginación.

Si seguís leyendo, en esta entrada exploraremos cómo el exceso de variables convierte los modelos en laberintos sin salida, donde ni el R² ni los errores de mínimos cuadrados pueden ayudarnos a escapar. Si alguna vez os habéis sentido perdidos entre números que prometen soluciones mágicas, esta es vuestra oportunidad para aprender a sortear las trampas del sobreajuste.

Vamos a intentar discernir cómo no perder el rumbo en el bosque de los datos.

Las nuevas tecnologías tienen la culpa

Hasta hace no mucho tiempo, lo habitual en biomedicina era manejar conjuntos de datos con un número variable de observaciones, pero con un número no muy elevado de variables en cada observación. Si llamamos “n” al número de observaciones y “p” al número de variables, p solía ser mucho menor que n.

En este contexto, la mayor parte de las técnicas estadísticas han sido diseñadas para funcionar bien en este ambiente de baja dimensionalidad, como le ocurre, por ejemplo, a la regresión lineal, técnica en la que nos vamos a centrar hoy.

Pero el progreso no perdona y, a lo largo de las últimas dos décadas, las nuevas tecnologías han cambiado de forma radical la forma en que obtenemos y procesamos la información en numerosos campos, incluido el de la biomedicina. De esta forma, no es nada raro disponer de conjuntos de datos en los que el número de variables (p) es grande, mientras que el de observaciones (n) es más reducido, ya sea por costes económicos o por dificultad de obtención de los datos.

Hace tres décadas podíamos intentar predecir la esperanza de vida analizando la relación entre peso, glucemia y presión arterial, por decir algo (n = 1000, p = 3). Por el contrario, hoy en día podemos tener interés en estudiar la relación con decenas o cientos de miles de mutaciones del ADN (los llamados polimorfismos, SNP), por poner otro ejemplo típico (n = 150, p = 3000).

Estos conjuntos de datos se han vuelto más anchos que largos o, dicho de forma elegante, se caracterizan por su alta dimensionalidad.

Uno podría pensar que esto es muy bueno, ya sabéis, más es mejor. Seguro que con más variables podemos detectar más patrones y asociaciones. Pero la cosa no es tan sencilla, ya que los métodos de control de las pruebas estadísticas clásicas pueden no funcionar muy bien en contextos de dimensionalidad alta y generar modelos predictivos totalmente inútiles.

El ejemplo de la regresión lineal

Vimos en una entrada anterior cómo se utiliza el método de los mínimos cuadrados para calcular el valor óptimo de los coeficientes de un modelo de regresión lineal. Podéis repasar el tema si no lo recordáis bien.

El problema con los mínimos cuadrados es que cuando p se aproxima, o supera, el valor de n, este método deja de funcionar tan bien y, aunque no haya relación real entre los datos, estimará unos valores de los coeficientes que proporcionarán un ajuste perfecto a los datos disponibles.

Los más atentos ya os habréis dado cuenta de que lo que el modelo hace es sobreajustar los datos, lo que tiene la desastrosa consecuencia de que no se podrá generalizar a datos nuevos. Pensadlo, los modelos se crean para hacer predicciones con datos nuevos no conocidos (los que utilizamos para elaborarlos ya los conocemos).

Para entender esto de una manera intuitiva, os muestro los dos gráficos de la primera figura.

A la izquierda podéis ver representado el caso más sencillo de la situación en que n = p. Tenemos dos variables y dos observaciones. Podéis ver que la recta de regresión hace un ajuste perfecto, pasando por las dos observaciones.

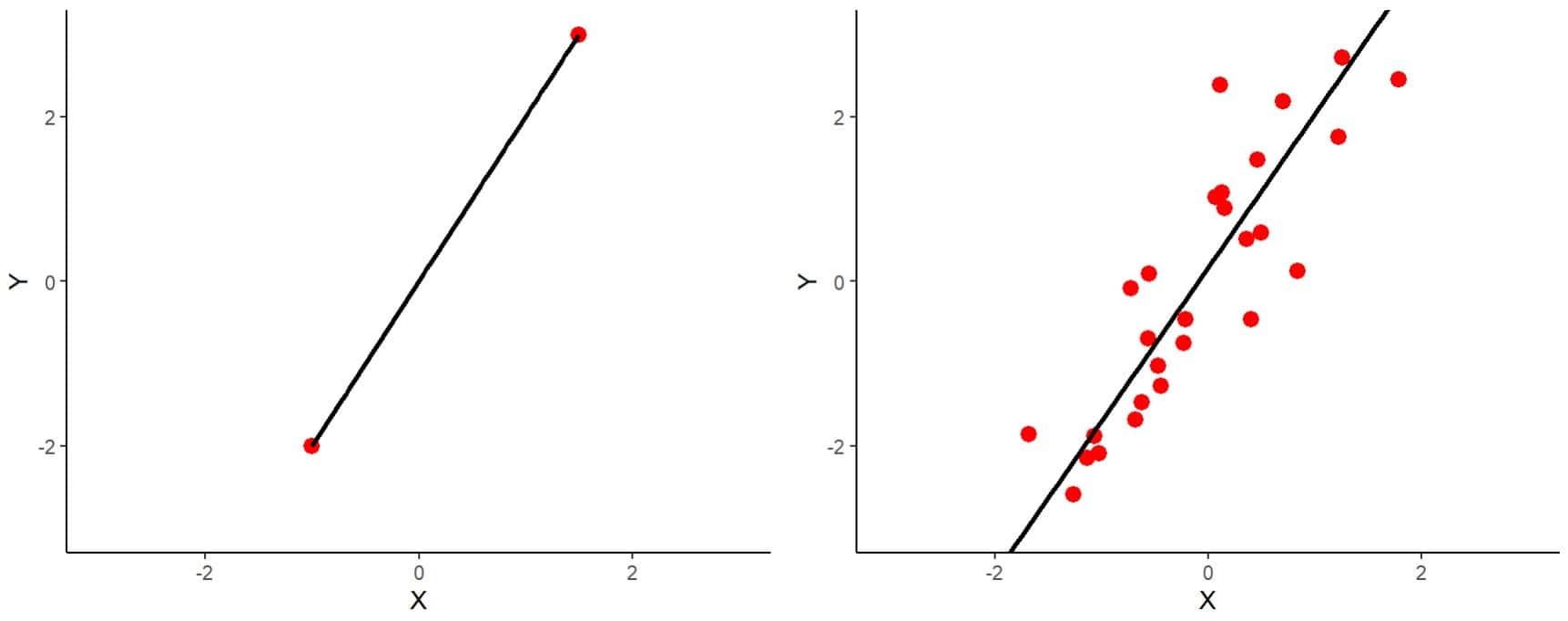
A la derecha tenéis un ejemplo similar, pero con 30 observaciones (n = 30, p = 2). Es evidente que la recta no puede pasar tan bien por todos los puntos como lo hacía en el otro ejemplo. El método de los mínimos cuadrados se encarga de calcular los coeficientes del modelo para que la recta pase lo más cerca posible de todos los puntos, minimizando los cuadrados de las distancias de los puntos a la recta.

Podría parecer que el primer modelo es mejor, pero pensemos qué ocurrirá cuando tengamos una observación nueva. En efecto, será más probable que se ajuste mejor el modelo de la derecha, con una relación n/p mayor. Pues esto mismo ocurre con un número mayor de observaciones y de variables. Nos encontramos ante la maldición de la dimensionalidad.

En conclusión, cuando el número de variables se aproxima o supera el número de observaciones, la ecuación de mínimos cuadrados es demasiado flexible y se produce un sobreajuste (overfitting para nuestros amigos angloparlantes).

Pero la cosa no acaba aquí. Tampoco funcionan bien los parámetros que utilizamos habitualmente para valorar la bondad del modelo, como el error medio de las estimaciones o el coeficiente de determinación.

La maldición de la dimensionalidad

Para mostraros esto último que hemos dicho, vamos a utilizar un ejemplo ficticio que me he inventado sobre la marcha utilizando el programa R. Los más aventureros podéis descargar el script completo en este enlace.

Para forzar un poco la situación, no mucho, he simulado un conjunto de datos con 100 observaciones y 100 variables (n = p = 100). Como suele ser habitual, he sido un poco tramposo y solo 10 variables tienen relación lineal con la variable objetivo. Las otras 90 variables son puro ruido aleatorio.

Una vez creado, divido los datos en dos subconjuntos, uno de entrenamiento (70 observaciones) para crear los modelos y uno de prueba (30 observaciones) para probarlos. Como es lógico, en estos dos subconjuntos el número de variables supera al de observaciones (n < p).

Por último, he ensamblado modelos consecutivos con un número creciente de variables predictivas, comenzando por cinco y metiendo cinco más en cada modelo consecutivo. Para todos ellos he calculado el coeficiente de determinación (R²), como indicador del rendimiento del modelo, y la suma de los cuadrados de los residuos (SSR), como indicador del error, tal como podéis ver en la segunda figura.

Fijémonos primero en las gráficas de color azul, que representan los dos parámetros obtenidos al elaborar los modelos con los datos de entrenamiento. Vemos como el R² va aumentando progresivamente al ir metiendo más variables predictivas en el modelo, de forma que alcanza un valor de 1 ya cuando incluimos unas 70 variables o más.

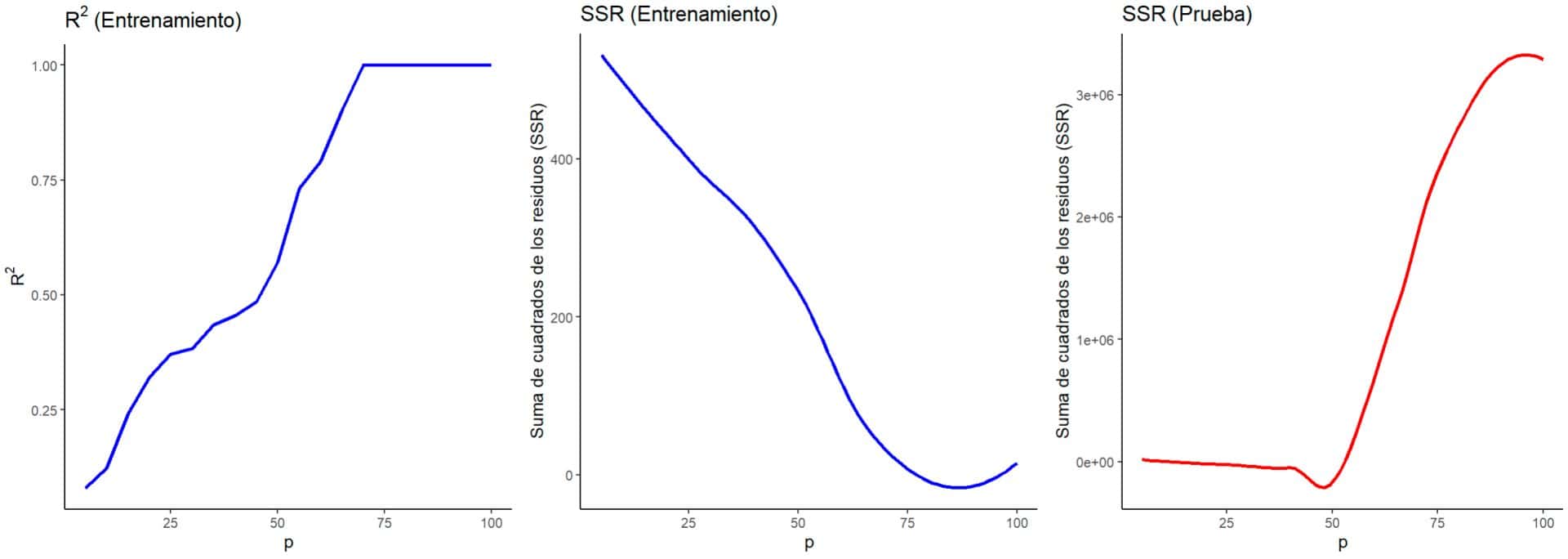
Algo similar ocurre con los errores del modelo (los SSR), que van disminuyendo hasta alcanzar casi el cero, más o menos en el mismo punto en el que R² se aproxima a 1.

Esto podría parecernos estupendo. Si R² representa el porcentaje de la varianza de los datos que es explicada por el modelo, un valor de 1 nos diría que el modelo es perfecto, ya que capta prácticamente toda la varianza de los datos, con un error que es prácticamente despreciable.

¿Cuál es el problema? Fijémonos ahora en la gráfica con la línea roja, hecha al probar los modelos con los datos de prueba, no utilizados para la propia elaboración del modelo. Podemos ver cómo el error del modelo al hacer las predicciones se dispara a partir de un determinado número de variables, en este caso unas 50 variables.

La interpretación es sencilla. Meter tantas variables en un modelo, la mayor parte de ellas no relacionadas con la variable que queremos predecir, provoca un sobreajuste del modelo a los datos de entrenamiento, pero una calamitosa ausencia de capacidad de generalizar las predicciones cuando le presentamos datos nuevos.

La lección para aprender es que tenemos que valorar de forma muy cuidadosa los resultados con conjuntos de datos con un número elevado de variables y no olvidar nunca, nunca, comprobar el rendimiento del modelo en un conjunto de datos independiente.

Como en otras muchas facetas de la vida, más no siempre es mejor y puede ser más importante la calidad que la cantidad, lo cual nos lleva a pensar en la posible solución de este problema.

La solución del problema

La solución al problema de la alta dimensionalidad es clara: reducir la dimensionalidad, para lo cual disponemos de numerosas posibilidades.

La más sencilla podría ser hacer una selección de variables con los métodos más tradicionales, como la selección progresiva hacia delante (forward stepwise selection, que dirían en Albión). También podríamos utilizar técnicas de regularización como la regresión lasso, que nos permite reducir el número de variables.

Por último, podemos aplicar técnicas de reducción de la dimensionalidad empleando análisis de componentes principales u otro tipo de algoritmos de aprendizaje automático, como árboles de decisión, para seleccionar un número reducido de variables que incluya aquéllas que verdaderamente son importantes para la construcción del modelo.

Nos vamos…

Y aquí lo vamos a dejar por hoy.

Hemos visto uno de los efectos de la llamada maldición de la dimensionalidad. Al contrario de lo que uno podría pensar, aumentar mucho el número de variables predictoras de un modelo puede ser contraproducente a la hora de crear un modelo que deba tener alguna capacidad predictiva.

Hay que seleccionar bien las variables, en particular cuando hay numerosas en relación con el número de observaciones, e incluir en el modelo solo aquellas que pueden influir de verdad en su capacidad de predicción. El resto de las variables solo aportarán ruido y contribuirán al riesgo de sobreajuste. Como siempre, habrá que buscar el equilibrio entre la capacidad de ajuste (el sesgo del modelo) y la capacidad de generalizar (la varianza del modelo).

Claro que esto resulta muchas veces más sencillo decirlo que llevarlo a la práctica. Puede ocurrir que algunas de las variables predictoras estén relacionadas entre sí, esto es, podemos enfrentarnos al problema de la multicolinealidad.

En estos casos, algunas variables podrán describirse como combinaciones lineales de otras variables, lo que nos dificultará averiguar cuáles son verdaderamente importantes para el modelo y nos impedirá estimar los mejores valores para los coeficientes de regresión. Pero esa es otra historia…