La V de Cramer.

Viajar es una de mis aficiones favoritas. Me encanta ver sitios nuevos y conocer las costumbres de la gente en los distintos países del mundo. Parece mentira que el mismo ser humano tenga hábitos tan diferentes en distintas localizaciones.

Para ilustrar lo que os cuento podemos ver datos sobre los pasatiempos favoritos y las bebidas predilectas de personas en dos países: Italia y Corea del Sur. Durante mis viajes por aquellos lugares pregunté y descubrí que, aunque las preguntas fuesen las mismas (actividad favorita entre cocinar, hacer deporte, leer, o salir con amigos, y bebida preferida entre café, vino o agua mineral), las respuestas parecían seguir patrones distintos en cada país.

En Italia, observé algo curioso: los amantes del café suelen preferir leer, mientras que quienes eligen el vino disfrutan más saliendo con amigos. Aquí parece haber una sincronía en los gustos, como si las combinaciones entre bebida y actividad fueran algo más que coincidencias. Sin embargo, en Corea del Sur, las elecciones son más dispersas y no parece haber un vínculo claro entre lo que alguien bebe y su pasatiempo. Los fans del café pueden disfrutar tanto de la cocina como de hacer deporte, sin ningún patrón claro.

Entonces, ¿cómo hacemos para poner números a esta aparente sintonía italiana frente al caos coreano? Claro, la prueba de ji-cuadrado nos dirá si existe alguna asociación entre bebida y actividad en cada país, pero eso solo nos da un “sí” o un “no”. ¿Qué pasa si queremos saber cuánto más fuerte es esa conexión en Italia que en Corea del Sur? Aquí es donde necesitamos algo con más chispa: la V de Cramer.

Esta herramienta no solo detecta si las variables están asociadas, sino que nos permite medir cuán intensa es esa relación en cada grupo, casi como poner un termómetro cultural. Así, podemos comparar la intensidad de las conexiones entre gustos en dos mundos distintos y descubrir cuánto de estas elecciones responde a patrones o es solo una cuestión de azar. ¡Es hora de cuantificar lo incuantificable!

La V de Cramer

Cuando pensamos en medir la fuerza de la asociación entre variables, es común que nuestra mente derive directamente a la utilización de coeficientes como el de correlación de Pearson o el de Spearman. Estas herramientas son perfectas para variables cuantitativas (el de Pearson), donde podemos trazar gráficos de dispersión y calcular tendencias lineales, así como para variables ordinales (el de Spearman). Pero ¿qué pasa si nuestras variables no son números continuos, sino categorías nominales sin relación de orden entre ellas?

Para este escenario, la estadística nos ofrece un héroe un poco menos conocido, pero igual de talentoso: la V de Cramer. Esta medida es ideal para evaluar la asociación entre dos variables nominales, como actividad favorita y bebida preferida, dándonos un número entre 0 (sin asociación) y 1 (asociación perfecta).

Algunos estaréis preguntándoos qué necesidad hay de complicarse la vida con la V de Cramer si podemos recurrir a otras medidas de asociación más conocidas, como el riesgo relativo. La razón es que la V de Cramer nos ofrece una interpretación más sencilla y elegante cuando las variables que tenemos que comparar tienen más de dos categorías.

Pensémoslo un momento. En el contexto clásico de una tabla 2×2, el riesgo relativo mide la razón entre las probabilidades de que ocurra el evento en los grupos expuestos a determinado factor y los no expuestos. Esto es simple y directo.

Sin embargo, cuando las variables tienen múltiples categorías, aunque podemos extender el cálculo de los riesgos relativos, ya no tendremos una sola cifra, sino varios riesgos relativos que interpretar, ya que habrá que valorar las comparaciones específicas para cada combinación de categorías, lo que dificulta resumir la relación en un solo valor. Es en estas situaciones en las que la V de Cramer brilla con luz propia, ya que condensa la relación en una sola cifra.

Eso sí, recordemos que las variables a comparar tienen que ser categóricas y no ordinales.

De italianos y coreanos

Vamos a volver a mis recuerdos de viaje para ilustrar cómo trabaja la V de Cramer.

Primero vamos a echar un vistazo a las tablas de contingencia, que os muestro en la siguiente figura. He coloreado las celdas de las tablas con un color más intenso al aumentar la frecuencia de cada celda. De esta manera, podemos ver a simple vista cuáles son las celdas más populares y, en consecuencia, la categorías de las dos variables que tienden más a asociarse.

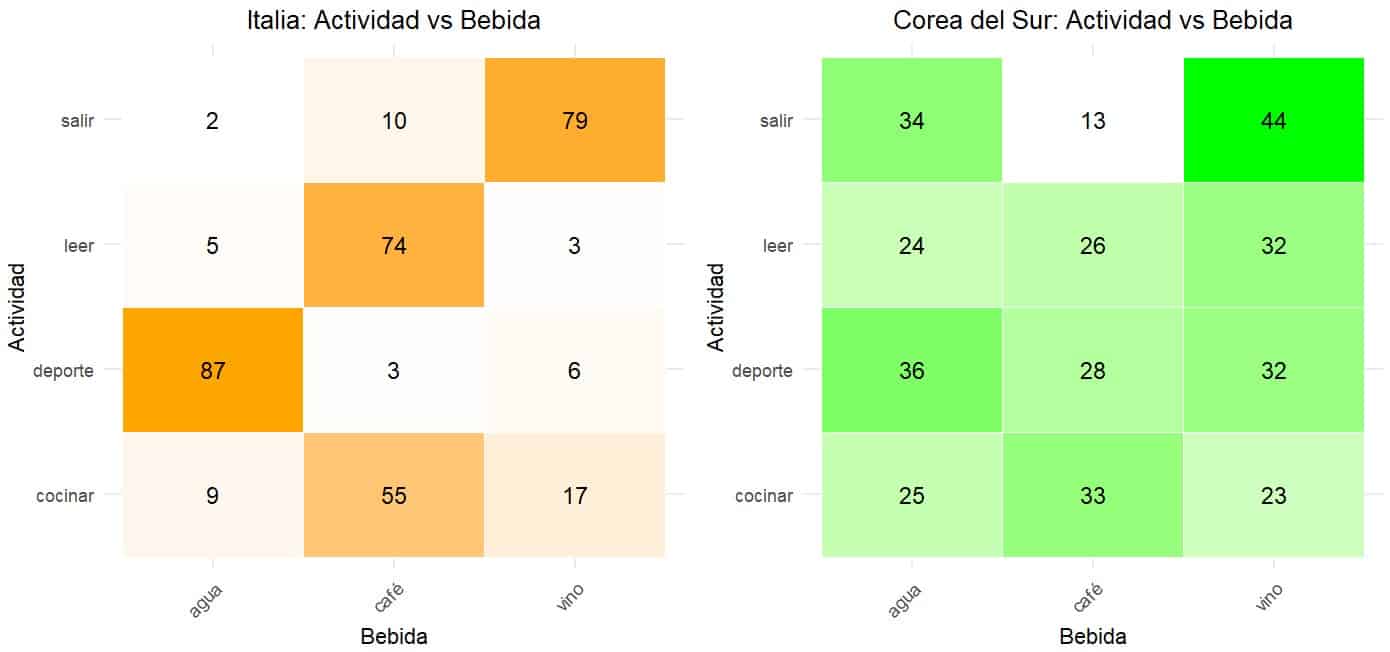
Fijémonos primero en la tabla de los italianos. Vemos que hay diferencias llamativas en la intensidad de los colores, lo que ya nos avisa de que algunas asociaciones son más frecuentes que otras.

Vemos, por ejemplo, que los que prefieren salir con amigos son más aficionados al vino. Por otra parte, los aficionados al deporte son más partidarios de beber agua. Esto no me sorprende lo más mínimo: los malos hábitos suelen asociarse con frecuencia. Para terminar el análisis italiano, vemos que los lectores y los cocineros suelen preferir el café.

Si pasamos a la tabla de los coreanos vemos que estas diferencias no son tan claras. Los colores de las celdas son mucho más uniformes, aunque parece que hay hábitos que se asocian algo más, como el deporte y el agua o lo poco que les gusta el café a los que prefieren ir de parranda con los amigos.

Este análisis está muy bien para andar por casa, pero ya sabéis que a mi me gusta cuantificar las cosas. Vamos a ver si podemos medir la fuerza de la asociación de estas combinaciones de costumbres que parecen existir cuando miramos números y colores.

Otra vez la V de Cramer

La V de Cramer es bastante sencilla de calcular. Tenemos que dividir el estadístico ji-cuadrado entre el producto del tamaño muestral y el número mínimo de grados de libertad entre filas y columnas. Por último, al resultado de todo esto le hacemos la raíz cuadrada.

Vamos primero con los italianos. Lo primero es calcular el valor del estadístico ji-cuadrado para una prueba de independencia. Os voy a ahorrar la fórmula, que tenéis en una entrada anterior. Yo lo he calculado con el programa R y obtengo un valor de 424,2, con 6 grados de libertad y un valor de p casi de 0, estadísticamente significativo.

Así que ya sabemos que hay una asociación significativa entre las dos variables nominales, la actividad favorita y la bebida preferente. Para cuantificar la fuerza de esta asociación, calculamos la V de Cramer. Ya sabemos el valor del estadístico ji-cuadrado (424,4) y podemos contar las frecuencias de la tabla para obtener el tamaño muestral (350). Como es una tabla 4×3, el número de grados de libertad mínimo de filas y columnas será 3 – 1 = 2. Hacemos la cuenta y obtenemos una V = 0,78.

Ya sabemos que la V de Cramer puede tener valores entre 0 y 1. En general, valores menores de 0,1 indican que no hay asociación, entre 0,1-0,3 la fuerza de la asociación es pequeña, entre 0,3-0,5 se dice que el efecto es moderado y, por último, cuando V es mayor de 0,5, se dice que las variables están fuertemente asociadas.

Ya hemos cuantificado la asociación en los italianos. El resultado nos corrobora la impresión que tuvimos al contemplar la tabla de contingencia: las dos variables muestran una fuerte asociación. Veamos ahora si los coreanos son tan caóticos como nos pareció al examinar su tabla.

Primero calculamos el valor del estadístico ji-cuadrado, que resulta ser de 17,56, con 6 grados de libertad y un valor de p = 0,007. Resulta que el caos no es tal, ya que sí vemos que las dos variables se asocian de manera estadísticamente significativa.

Eso sí, suponemos que la V de Cramer tendrá un valor mucho más bajo que la de los italianos. En efecto, si hacemos el cálculo vemos que vale 0,16, con lo que concluimos que la fuerza de asociación de estas dos variables en Corea del Sur es muy baja.

Nos vamos…

Y hasta aquí hemos llegado.

No me gustaría terminar sin advertir al público que los datos que hemos utilizado en la entrada son totalmente ficticios. Que me perdonen los italianos y los coreanos del sur si alguno se siente ofendido por la asignación de actividad o de bebida favorita.

En cualquier caso, hemos visto cómo valorar si dos variables categóricas nominales se asocian de una manera casi coreografiada o si, por el contrario, presentan un mosaico más caótico, mostrando como los números, que también tienen su sabor cultural, nos permiten cuantificar la asociación de manera casi quirúrgica.

Este ejemplo me da por pensar si la asociación y el azar se pueden también explorar en otras áreas de la vida, como la elección de una pareja o el éxito en taquilla de una película. Al fin y al cabo, la magia de la probabilidad está por doquier. Existen otras técnicas que no hemos mencionado en esta entrada, como la regresión de Poisson, que pueden ayudarnos a predecir fenómenos inesperados o a decodificar correlaciones espurias. Pero esa es otra historia…