Prueba de la U de Mann-Whitney

La prueba de la U de Mann-Whitney, también denominada prueba de la suma de rangos de Wilcoxon, es una prueba no paramétrica que permite comparar las medianas de una variable cuantitativa para las dos categorías de una variable cualitativa dicotómica. Se aplica cuando no se pueden asumir los supuestos necesarios para utilizar la prueba de la t de Student.
Definitivamente, dos formas diferentes de ver el mundo y no solo una elección que todo estudiante tiene que hacer llegado el momento.
Aquellos más interesados en explicar los fenómenos físicos y de la naturaleza, sin duda, elegirán ciencias. Por su parte, los que tengan más interés por intentar comprender a sus congéneres, los llamados seres humanos, serán candidatos a las letras.
Y no penséis que esta es una cuestión solo de nuestros tiempos. Ya se planteaba en las primeras universidades del siglo XIII, donde uno podía elegir entre trívium (gramática, dialéctica y retórica) y quadrivium (aritmética, geometría, astronomía y música). Ya veis, las siete artes liberales divididas en las dos categorías: ciencias y letras.
Y todo esto me viene a la cabeza por un problema que me planteó el otro día un cuñado que tengo, que es maestro. Resulta que quiere saber si sus alumnos están más preparados para escoger ciencias o letras el próximo curso.
Para tener algo en qué basarse, ha tomado las notas de los exámenes de matemáticas de una muestra de la clase y las de historia de otra muestra de otros alumnos de la clase, y quiere analizarlas para ver para qué están más cualificados los alumnos de la clase. El problema de mi cuñado es que él es de letras, así que no tiene ni idea de cómo hacerlo y no se le ha ocurrido otra cosa que recurrir a mí, que soy de ciencias.
Veamos cómo podemos resolver el problema.
Planteamiento del problema
Las notas de los alumnos de mi cuñado en los dos exámenes son las que veis a continuación:
– Matemáticas (M): 5, 7, 9, 3, 10, 6, 7, 8, 7 y 2.
– Historia (H): 6, 8, 7, 9, 5, 10, 10, 5, 4 y 8.
¿Qué os parece? ¿Se les dan mejor las ciencias o las letras?
Viendo las 20 calificaciones es difícil contestar a la pregunta. Parece que las notas son bastante uniformes en los dos exámenes.
Si calculamos la media, veremos que es de un 6,4 en mates y de un 7,2 en historia. Casi un punto más alta la nota de historia, así que nos inclinaríamos por las letras.
De todas formas, empezamos a dudar si la media es la medida de centralización más adecuada para este problema. Vemos que hay medidas extremas (dieces y algún 2) que pueden sesgar el valor de la media, sobre todo en esta muestra tan pequeña. Así que calculamos las medianas, que son de 7 en matemáticas y 7,5 en historia.
Vemos que se mantiene una pequeña diferencia a favor de las notas de historia, pero, claro, se trata de una muestra muy pequeña y la diferencia no es muy grande, así que esta diferencia podría deberse a la casualidad y, en realidad, que los alumnos tuviesen un rendimiento similar en ambas asignaturas.
Necesitamos hacer un contraste de hipótesis para saber la probabilidad de obtener una diferencia como la observada por causa del azar.
Prueba de la U de Mann-Whitney
Ya vimos en una entrada anterior que la elección de la prueba estadística de contraste depende, entre otros factores, del tipo de variables que queramos contrastar.
En nuestro ejemplo, queremos comparar las medias (variable cuantitativa) para las dos categorías de una variable cualitativa (asignatura, con dos categorías: M y H). La prueba de primera elección es la de la t de Student para comparación de dos medias independientes.
Sin embargo, para poder hacer una t de Student, la variable cuantitativa debe distribuirse de forma normal para las dos categorías de la variable cualitativa, cosa que dudamos que se cumpla en nuestro caso.
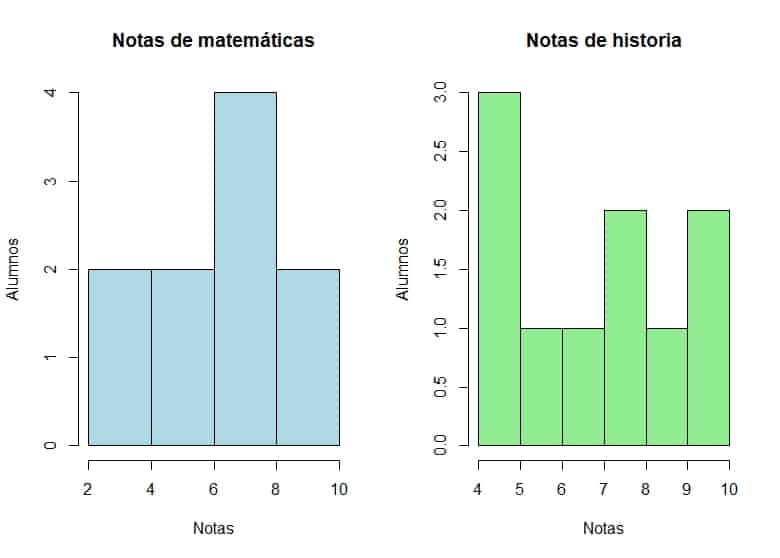
Hay varias formas de comprobar la normalidad. En este caso, la más sencilla es dibujar los histogramas de las notas de las dos asignaturas, que podéis ver en la figura adjunta.
Viendo los gráficos ya no tenemos necesidad de hacer más pruebas. Parece claro que las variables no se distribuyen de forma normal. Por si teníamos alguna duda con una muestra tan pequeña, queda claro que no podemos hacer una t de Student. ¿Qué podemos hacer? Recurrir a la alternativa no paramétrica, que es la prueba de la U de Mann-Whitney, también llamada prueba de la suma de rangos de Wilcoxon.
Fundamento de la prueba de la U de Mann-Whitney
Como prueba no paramétrica que es, la prueba de la U de Mann-Whitney requiere ordenar los rangos de los resultados de la variable dependiente, por lo que no compara medias, sino medianas.
La gran ventaja de esta prueba es que está libre de los requisitos y supuestos de las pruebas paramétricas. Su inconveniente es que es menos potente que la alternativa paramétrica, por lo que costará más alcanzar nuestra deseada p < 0,05.
La sistemática para realizar el contraste precisa de los siguientes pasos:
1. Ordenar por rangos los resultados de la variable continua para las dos categorías combinadas.
2. Sumar los rangos de las dos categorías por separado.
3. Comparar los dos resultados para decidir si la diferencia se debe al azar.
Vamos a ver estos tres pasos.
Ordenar los rangos
Si ordenamos las calificaciones de los dos exámenes, obtendremos el listado siguiente:
– M: 2, 3, 5, 6, 7, 7, 7, 8, 9 y 10.
– H: 4, 5, 5, 6, 7, 8, 8, 9, 10 y 10.
A continuación, agrupamos en una sola lista ordenada los rangos de las calificaciones de las dos asignaturas, tal como podéis ver en la figura 2.
Una vez combinados, vamos a ordenar del 1 al 20 las calificaciones, siendo 1 la calificación más baja y 20 la calificación más alta, como veis en latabla siguiente:

El problema es que hay más de un alumno que saca la misma calificación. Por ejemplo, hay 3 alumnos que sacan un 5, uno en matemáticas y dos en historia, en las posiciones cuarta a sexta. Para no discriminar a ninguno de ellos y darles el mismo número de orden (el mismo rango), vamos a calcular el rango medio de los tres y decir que los tres alumnos están en posición quinta.
Hacemos lo mismo con todas las notas, tal como veis en la figura, obteniendo finalmente la lista de rangos combinados ordenados, como muestra la fila inferior de la tabla.
Sumar los rangos
La prueba de la U de Mann-Whitney asume la hipótesis nula de que las medianas de los dos grupos son iguales. En el caso de que el valor de p sea menor de 0,05, rechazaremos la hipótesis nula y asumiremos que las medianas son diferentes.
¿Cómo se relaciona esto con las listas de rangos ordenados que hemos construido? Si lo pensamos un poco, si los dos grupos son similares, tendrán un número similar de elementos en la primera posición, en la segunda, etc. De esta forma, si sumamos los rangos de cada grupo, el valor de la suma debe ser similar si se cumple la hipótesis nula de igualdad de medianas.
Sumemos los rangos en nuestro ejemplo:
– M: 1 + 2 + 5 + 7,5 + 10,5 + 10,5 + 10,5 + 14 + 16,5 + 19 = 96,5.
– H: 3 + 5 + 5 + 7,5 + 10,5 + 14 + 14 + 16,5 + 19 + 19 = 113,5.
Vemos que la suma de rangos es mayor en el examen de historia. Como los rangos mayores son los de las notas más altas, esto quiere decir que las notas son mejores en historia que en matemáticas. Los alumnos de mi cuñado están más dotados para las letras.
¿Seguro?
Comparar las sumas de rangos
No podemos estar seguros solo con ver la diferencia entre 113,5 y 96,5. Tenemos que calcular la probabilidad de que, si son iguales, el azar explique esta diferencia.
De forma interna, la prueba de la U de Mann-Whitney, con unas fórmulas que son tan antipáticas que no las vamos a poner aquí, calcula un estadístico U y, a partir de ese valor de U, un valor z (que sigue una distribución normal) con el que ya se puede calcular el valor de p.
Una alternativa es buscar una tabla de valores críticos de la diferencia de las sumas de rangos, de las que podéis encontrar en Internet o en los libros de Estadística. Yo os muestro un ejemplo en latabla adjunta.

En esta tabla podéis ver los valores críticos para dos muestras (n1 y n2) con un contraste bilateral y un nivel de significación de 0,05.
En nuestro caso, este valor es de 23. Eso quiere decir que toda diferencia menor de 23 puntos será explicada por el azar con una probabilidad mayor de 0,05. Eso sí, si la diferencia es mayor de 23, la probabilidad de que sea por azar será tan baja que nos la creeremos. En otras palabras, será estadísticamente significativa.
La diferencia que hemos observado nosotros es de 113,5 – 96,5 = 17. Como nuestra diferencia no alcanza el valor crítico de 23, podemos concluir que la diferencia encontrada no es estadísticamente significativa. No sabemos el valor exacto de p, pero seguro que está por encima de 0,05, con lo que no podemos rechazar la hipótesis nula de igualdad de medianas.
Una forma más sencilla de hacer el mismo cálculo
Todo esto que hemos visto hasta ahora es muy instructivo para comprender cómo funciona la prueba de la U de Mann-Whitney, pero a nadie se le ocurre hacer todos estos cálculos de forma manual, como os he mostrado.
Vamos a ver cómo podemos facilitar todo el proceso utilizando un programa estadístico, tal como el programa R. Lo haríamos en los siguientes pasos:
1. Introducimos las calificaciones de las dos asignaturas, matemáticas (M) e historia(H):
notaM <- c(5, 7, 9, 3, 10, 6, 7, 8, 7, 2)
notaH <- c(6, 8, 7, 9, 5, 10, 10, 5, 4, 8)
2. Combinamos todas las notas de forma sucesiva en un solo vector:
notas <- c(notaM, notaH)
3. Creamos las etiquetas de cada asignatura:
asignatura <- c(rep("M",10), rep("H", 10))
4. Obtenemos el vector de rangos ordenados de menor a mayor:
rangos <- rank(notas)
5. Calculamos las sumas de los rangos para cada asignatura:
tapply(rangos, asignatura, sum)
R vuelve a darnos los mismos valores, 113,5 para historia y 96,5 para matemáticas. Ya solo tendríamos que restar y ver en la tabla si supera el valor crítico.
La forma recomendada de hacerlo
Para acabar, vamos a ver la forma recomendada de hacerlo. Aunque se utilice un programa de estadística, no es recomendable hacer esto a mano. Lo recomendable es usar la función que ya tendrá el programa para realizar la prueba de la U de Mann-Whitney.
Además de la simplicidad, obtendremos así el valor exacto de p y no tendremos que recurrir a ninguna tabla para decidir si aceptamos o rechazamos la hipótesis nula.
Una vez introducidos los datos, como vimos en el punto anterior (notaM y notaH), ya solo nos quedaría escribir:
wilcox.test(notaM, notaH)
R nos dará un valor del estadístico W de 41,5, al cual le corresponde un valor de p = 0,54.
Al ser el valor de p mayor que 0,05, no podemos rechazar la hipótesis nula, con lo que tendremos que asumir que la pequeña diferencia entre las notas de las dos asignaturas es debida al azar. Mi cuñado puede estar tranquilo, ha preparado bien a sus alumnos para que elijan lo que más les guste.
Nos vamos…
Y aquí terminamos por hoy.
Hemos visto cómo podemos comparar dos medias cuando no se cumplen los supuestos necesarios para realizar una prueba paramétrica. Bueno, en realidad no compararíamos ya dos medias, sino los rangos de los valores para las dos categorías de la variable cualitativa.
Viendo cómo se hace de forma manual nos queda claro también porqué a la prueba de la U de Mann-Whitney se le llama también prueba de la suma de rangos de Wilcoxon (no se debe confundir con la prueba de los rangos con signo de Wilcoxon). ¿Y por qué estos dos nombres? Pues porque hay dos métodos de hacer este contraste, aunque aquí solo hemos visto uno de ellos.
¿Y qué pasaría si queremos añadir a la comparación las notas de otra u otras asignaturas? En este caso, tendríamos que recurrir a la alternativa no paramétrica del análisis de la varianza, que no es otra que la prueba de Kruskal-Wallis. Pero esa es otra historia…
