Análisis de un modelo de regresión logística.

¡Ah, el misterioso y caprichoso aire! Un alborotador nato que nos deja perplejos con sus paradójicas travesuras. En casa, es el eterno enemigo de nuestros planes de mantenernos saludables; basta con una ligera corriente de aire para que nos transformemos en seres temblorosos y resfriados. Es como si el aire estuviera conspirando con los pañuelos de papel para mantenerse en el negocio.

Pero ¡esperad! Cuando llegamos a la playa, el aire se convierte en nuestro aliado de bronceado. Cada ráfaga juega a ser un hábil artista que dora nuestra piel bajo el sol. Parece que el aire cambia su personalidad como un camaleón, pasando de ser el Dr. Jekyll gélido en casa al Sr. Hyde tostado en la playa. ¿Será que el aire tiene una doble vida? ¡Quién lo diría!

Y así, queridos amigos, mientras el aire sigue con su juego de contrastes, nosotros hoy nos vamos a adentrar en el análisis de los modelos de regresión logística múltiple. Aunque en este caso no encontraremos paradojas misteriosas, sí descubriremos la magia de cómo esta herramienta estadística puede ayudarnos a evaluar y valorar la calidad de los modelos predictivos.

Una vez más, trataremos de ver qué es necesario para saber si un modelo predictivo puede ser capaz de convertir la incertidumbre en precisión.

Modelo de regresión logística múltiple

Ya vimos en entradas anteriores cómo los modelos de regresión intentan predecir el valor de una variable dependiente conociendo el valor de una o más variables independientes o predictoras.

Hoy vamos a centrarnos en la regresión logística múltiple, cuya ecuación general es la siguiente:

ln(Odds_Y) = b₀ + b₁X₁ + b₂X₂ + … + b_nX_n,

en la que, Y es el valor de la variable dependiente binaria, b₀ es la constante del modelo (equivale al valor de la variable dependiente cuando todas las independientes valen cero o cuando no hay efecto de las variables independientes sobre la dependiente), b_i los coeficientes de cada variable independiente (representan el cambio en la probabilidad de que ocurra el evento de interés por cada unidad de cambio en la variable independiente X_i) y X_i dichas variables independientes.

La variable dependiente binaria puede ser cualquier evento que ocurra o no ocurra, como, por ejemplo, que te toque o no la lotería. Las variables independientes pueden ser cualquier característica de los sujetos que se cree que está relacionada con la variable dependiente, como, por ejemplo. si juegas a la lotería, cuánto juegas, con qué frecuencia y si eres un gafe o una persona afortunada.

La probabilidad se estima utilizando una función logística, que es una función que mapea valores reales al rango [0, 1]. Si calculamos el antilogaritmo natural (o, lo que es lo mismo, le aplicamos la función exponencial) obtendremos la odds de que ocurra el suceso etiquetado como 1. Ya solo nos quedará calcular la probabilidad a partir de la siguiente fórmula:

P = Odds / (Odds + 1)

Un ejemplo práctico

Para explicar cómo interpretar los resultados de un modelo de regresión logística, vamos a utilizar un ejemplo realizado con un programa estadístico concreto, el programa R. Vamos a elaborar un modelo de regresión logística múltiple y analizar todos los resultados que el programa nos ofrece sobre el modelo.

Como es lógico, la salida de resultados variará en función del programa de estadística que empleemos, pero básicamente tendremos que analizar los mismos parámetros con independencia de cuál utilicemos.

Para que podáis replicar lo que vamos a contar, usaremos el conjunto de datos “Melanoma”, incluido en el paquete “MASS” de R.

Este conjunto contiene los datos de 205 pacientes afectos de melanoma y recoge una serie de variables: tiempo de supervivencia en días (time), estado de supervivencia (status, codificado como 1: muerte por melanoma, 2: vivo, 3: muerte por otra causa), género (sex, codificado como 1: hombre, 0: mujer), edad en años (age), año de la intervención (year), grosor del tumor en milímetros (thickness) y presencia de ulceración en el tumor (ulcer, codificado como 1: presencia, 0: ausencia).

Lo primero que haremos, una vez abierto R, es instalar el paquete, si no lo hemos hecho previamente. Acto seguido cargamos la biblioteca MASS y el conjunto de datos:

install.packages(“MASS”)

library(MASS)

data(Melanoma)

Este es un estudio de supervivencia pero, para simplificar, vamos a obviar los datos censurados y el tiempo en el que ocurre el evento (status). Además, vamos a convertir la variable status en una dicotómica codificada como 1 si se ha producido la muerte por melanoma y 0 si está vivo o se ha muerto por otra causa (no muerto por melanoma). Usamos el siguiente comando:

Melanoma$status <- ifelse(Melanoma$status == 1, 1, 0)

Una vez que tenemos los datos preparados, vamos a tratar de averiguar cuáles de las variables recogidas en el registro influyen sobre la probabilidad de muerte por melanoma, ya sea aumentándola o disminuyéndola, y en qué grado lo hacen. Para ello, construimos el modelo de regresión logística múltiple, según el comando siguiente:

model <- glm(status ~ time + sex + age + year + thickness + ulcer, data = Melanoma, family = binomial(link = "logit"))

El modelo se guarda en una variable llamada “model”. Para ver la información disponible, la forma más sencilla es ejecutar el comando summary(model). Podéis ver el resultado en la figura adjunta, que incluye información sobre los coeficientes, la significancia estadística, la calidad y la bondad de ajuste del modelo.

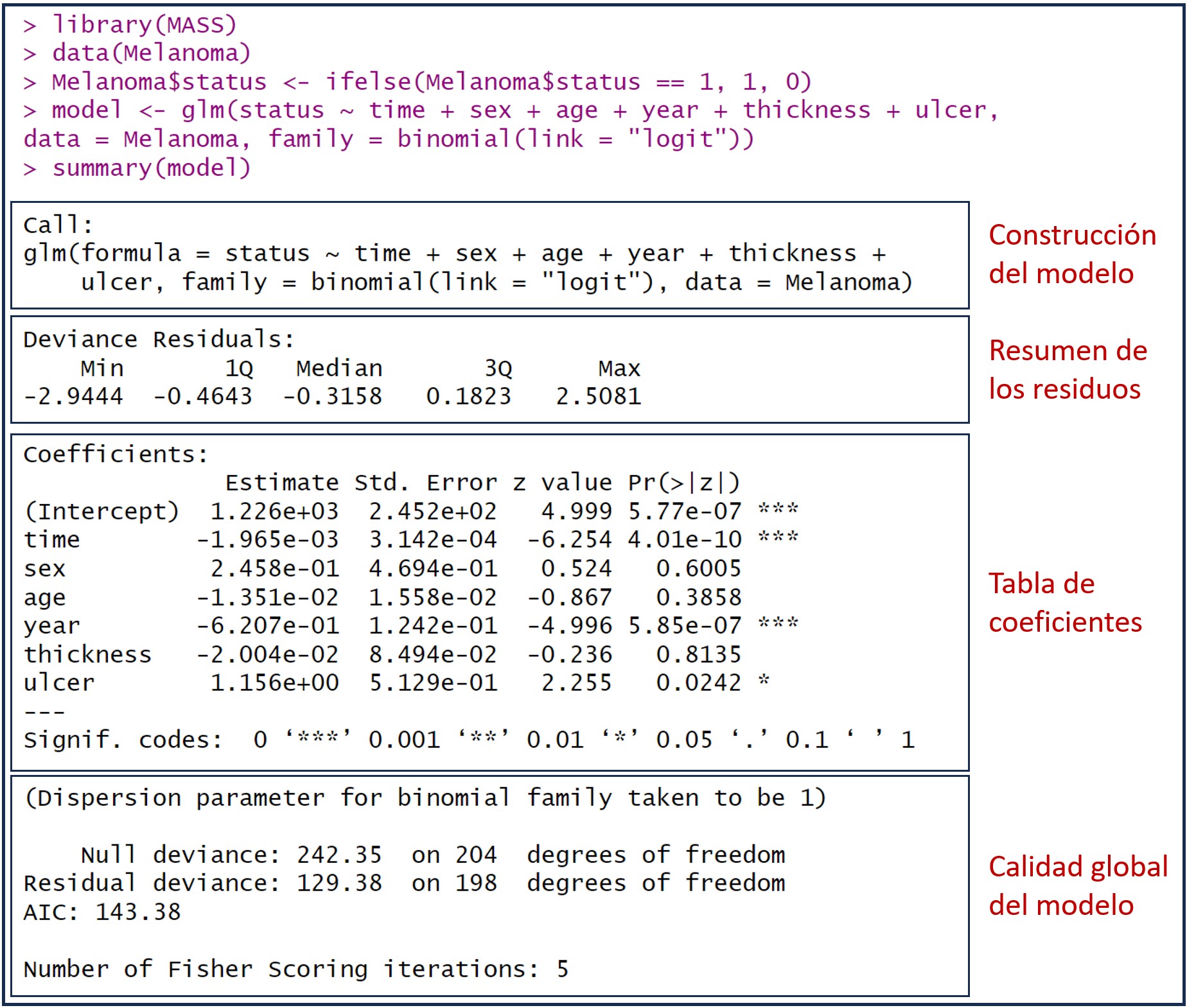
En la figura he añadido unos recuadros para separar los diferentes aspectos de la información del modelo que R nos proporciona. Vamos a verlos uno a uno.

Construcción del modelo

Lo primero que nos muestra la función summary() es la fórmula utilizada para construir el modelo. Este es el momento para revisar que la fórmula es la correcta, que hemos incluido en el modelo todas las variables independientes que deseamos y que hemos utilizado el conjunto de datos adecuado.

Según la sintaxis de R, la función glm() incluye la fórmula con la variable dependiente a la izquierda del símbolo “~” y la suma de las independientes a su derecha. Seguidamente se especifica el conjunto de datos utilizado. Más a la derecha, el término family especifica la distribución que asumimos sigue la variable dependiente, que en este caso es una binomial.

Por último, se establece la función de enlace (link), que se utiliza para convertir la variable dependiente en una escala que sea más fácil de trabajar. La función de enlace más común para la regresión logística es la función logit, que toma el valor de la variable dependiente (un valor real cualquiera) y lo convierte en una probabilidad comprendida entre 0 y 1.

Resumen de los residuos de desviación

Los residuos de desviación, también llamados residuos de Pearson, son el análogo de los residuos del modelo de regresión lineal y reflejan las diferencias entre los valores reales de la variable dependiente y los valores predichos por el modelo. La diferencia es que la variable dependiente en la regresión lineal es continua, mientras que en la regresión logística es binaria, por lo que el cálculo de los residuos de desviación se basa en la log-verosimilitud en lugar del método de la suma de los cuadrados de los errores.

Hagamos un pequeño inciso para aquellos que no entiendan bien qué significa esto de la log-verosimilitud.

La verosimilitud es una medida de la probabilidad de observar un conjunto de datos dado un conjunto de parámetros en el modelo. Habitualmente es más sencillo trabajar con los logaritmos, calculándose la log-verosimilitud como la suma de los logaritmos de las probabilidades de obtener cada dato real observado, dados los parámetros del modelo. Su fórmula, para los amantes de las emociones fuertes, es la siguiente:

L(β) = ∑ [ y_i * log(p_i) + (1 – y_i) * log(1 – p_i) ]

No os asustéis, en realidad no es tan antipática como parece. L(β) representa la función de log-verosimilitud, que nos interesará que sea lo mayor posible (mejor ajuste del modelo). y_i representa el valor de la variable dependiente para la observación i, y p_i es la probabilidad estimada por el modelo de que se produzca el evento de interés (codificada como 1 en la variable dependiente).

El objetivo en la regresión logística es encontrar los valores óptimos de los parámetros β que maximicen la función de log-verosimilitud (el modelo se ajusta mejor a los datos observados), de lo que se encarga el algoritmo de máxima verosimilitud.

Una vez dicho esto, volvamos con nuestros residuos. Vemos que el programa nos proporciona los valores máximo y mínimo, además de los tres cuartiles: el primer cuartil (el límite superior del 25% de los residuos ordenados de menor a mayor), la mediana o segundo cuartil (que deja a cada lado el 50% de los residuos) y el tercer cuartil (límite superior del 75% de los residuos).

La valoración de la distribución de los residuos es también algo diferente a la de la regresión lineal. Aunque la media de los residuos no es obligatoriamente cero, una mediana cercana a cero sí que indica que los residuos están distribuidos simétricamente alrededor de cero y que el modelo tiene una buena capacidad de predicción.

Por otra parte, aunque depende en parte del contexto de aplicación del modelo, un valor más negativo del primer cuartil sugiere que el modelo está sobreestimando la probabilidad de que ocurra el evento de interés (variable dependiente codificada como 1).

De manera similar, un valor más positivo del tercer cuartil sugiere que el modelo está subestimando la probabilidad de que ocurra el evento de interés. Además, a mayor diferencia entre los cuartiles primero y tercer (mayor recorrido intercuartílico), menor precisión tendrá el modelo.

En resumen, nos interesa obtener un modelo con una mediana de los residuos cercanos a cero y distribuidos simétricamente para tener una mejor capacidad de predicción. Cuanto más centrado alrededor de cero, mayor precisión en las predicciones.

Si aplicamos lo dicho a nuestro ejemplo, parece que el modelo no tiene muy buena capacidad de predicción y que, probablemente, sobreestima la probabilidad de que ocurra el evento de interés, la mortalidad por melanoma.

La tabla de coeficientes

Después de la distribución de los residuos, se nos muestra la tabla de los coeficientes de regresión del modelo, con los coeficientes en las filas y una serie de columnas:

1. Nombre de la variable.

2. Valor estimado del coeficiente de regresión (estimate).

3. El error estándar del coeficiente (Std. Error), que nos permite calcular su intervalo de confianza).

4. La medida de significación estadística de cada coeficiente estimado, en forma del valor de z (z value). El valor z se calcula dividiendo el valor estimado del coeficiente entre su error estándar. Proporciona una indicación de cuántas desviaciones estándar se aleja el coeficiente estimado de cero (el supuesto de la hipótesis nula es que los coeficientes no son distintos de 0). En general, cuanto mayor sea el valor absoluto del valor z, más significativo es el coeficiente.

5. El valor de p (Pr(>|z|)), que nos dice la probabilidad de encontrar un valor de z tan alejado o más de 0 solo por azar. Como ya sabemos, lo habitual es considerar esta diferencia como estadísticamente significativa cuando p < 0,05.

Aquellos coeficientes que son estadísticamente significativos se corresponden con las variables que contribuyen a explicar la variabilidad del modelo. Los que tienen valor negativo se correlacionan de forma negativa con la odds (y, por tanto, con la probabilidad) de que se produzca el evento de interés. A su vez, los positivos lo hacen de forma positiva.

Al igual que ocurre con la regresión lineal, los coeficientes de regresión pueden verse sesgados por la presencia de colinealidad. Una pista que nos puede hacer sospechar que haya colinealidad es la presencia de coeficientes anormalmente grandes en comparación con los demás, de signo opuesto al que nos parecería que debería tener por nuestro conocimiento del contexto en el que se aplica el modelo, o con un error estándar muy alto.

La interpretación de los coeficientes de regresión logística es un poco más complicada que la de la lineal, ya que representan el cambio en el logaritmo de la odds ratio (OR) de que un evento ocurra (la categoría 1 de la variable dependiente) en respuesta a un cambio unitario en la variable independiente del coeficiente, manteniendo constantes las demás variables independientes del modelo.

Dicho de una forma más precisa, aunque quizás menos comprensible, representa el cambio en log-verosimilitud para cada aumento unitario de la variable independiente a la que corresponde el coeficiente.

Por lo tanto, para calcular la OR de una variable tendremos que aplicar la función exponencial (el anti-logaritmo natural) al coeficiente de regresión de esa variable (lo que solo tiene sentido si es estadísticamente significativo).

Echemos un vistazo a nuestro modelo. Tenemos el intercepto y 6 variables independientes, pero solo alcanzan significación estadística el intercepto, el tiempo de supervivencia en días (time), el año de la intervención (year) y la presencia de ulceración en el tumor (ulcer, codificado como 1: presencia, 0: ausencia).

El tiempo de supervivencia en días, variable cuantitativa, tiene un coeficiente de correlación de -0.001965. Si le aplicamos la función exponencial (exp(-0.001965)) obtenemos una OR de 0,998. Como podemos ver, un coeficiente negativo (que equivale a una OR menor de 1) indica que la variable disminuye la probabilidad de que se produzca el evento (muerte por melanoma). Además, es estadísticamente significativo, por lo que parece que el tiempo de supervivencia es una variable importante. ¿Cuál es el problema?

El problema es que aquellos coeficientes muy pequeños nos darán OR próximas a 1, el valor nulo de la OR. En general, una OR cercana a 1 sugiere que la variable no es un predictor fuerte del evento de interés y que su efecto en la probabilidad es prácticamente despreciable. En este caso, la variable puede no ser relevante para el modelo, y su inclusión podría no aportar mucha información o mejora en la capacidad predictiva, aunque tenga significación estadística.

Claro que todo esto hay que valorarlo en el contexto. Debido a la naturaleza logarítmica del modelo de regresión logística, la magnitud del efecto de supervivencia en días puede ser más importante cuando el valor del número de días es mayor. Si se codifica el tiempo en meses en lugar de días, el coeficiente seguirá siendo el mismo en términos de log-verosimilitud, pero la interpretación de la OR asociada cambiará en función de la nueva escala.

Veamos la interpretación del efecto de la variable ulceración (ulcer). Su coeficiente es 1,156, cuya exponencial (OR) es de 3,18. Al ser un coeficiente positivo nos dará una OR mayor que 1, por lo que su presencia (el valor codificado como 1) aumenta el riesgo de muerte por melanoma. Concretamente, es unas 3 veces más probable fallecer a causa del melanoma cuando este está ulcerado que cuando no lo está.

Resumen de la calidad global del modelo

La última parte de la salida de resultados de la función summary() nos muestra las estadísticas de calidad del modelo global. Es muy importante comprobar la calidad de los indicadores de este apartado antes de aplicar el modelo y no basarse únicamente en la significación estadística de los coeficientes de regresión.

En primer lugar, R nos da un mensaje sobre la dispersión de la función binomial, que ha establecido en 1. Veamos qué quiere decir esto.

Hemos asumido que la variable dependiente sigue una distribución binomial (muerte por melanoma o no-muerte por melanoma) y hemos utilizado la función de enlace logit para modelar las probabilidades de que ocurra el enlace de interés. Pues bien, para la familia binomial se asume que la dispersión es constante y que los datos se ajustan adecuadamente al modelo, lo que implica que la varianza de la distribución binomial se mantiene constante en todo el rango de valores predichos por el modelo.

Cuando la dispersión se establece en 1, significa que la varianza de los datos se ajusta bien al modelo binomial estándar. Si hubiera sobre-dispersión (varianza mayor que 1) o subdispersión (varianza menor que 1), el valor del parámetro de dispersión se ajustaría en consecuencia para reflejar dicha variabilidad adicional o reducida. Por tanto, lo que nos está diciendo R es que la varianza se ajusta adecuadamente al modelo de regresión logística binomial estándar.

A continuación de este comentario sobre la dispersión, se muestran una serie de parámetros que tenemos que valorar:

1. La desviación de los residuos y del modelo nulo (null and residual deviances). Son dos medidas que nos sirven para valorar la bondad de ajuste del modelo y comparar su capacidad predictiva con la del llamado modelo nulo, que sería aquel que solo contiene el término del intercepto y no considera ninguna variable explicativa o independiente para predecir la variable dependiente.

Si lo pensamos un poco, esto significa que todas las observaciones se agruparían en una sola categoría de la variable dependiente. Esto permite que el modelo nulo sirva como referencia para comparar el rendimiento de modelos más complejos que incluyen variables independientes.

La desviación representa las diferencias entre las predicciones del modelo y el valor real observado de la variable independiente. La desviación nula representa las discrepancias cuando se ajusta el modelo nulo, mientras que la desviación residual es la que se obtiene con el modelo en el que incluimos las variables independientes o predictoras.

Si comparamos la desviación residual de nuestro modelo con la desviación del modelo nulo, podemos ver que esta disminuye, lo que indica que se mejora la capacidad de predicción del modelo. En nuestro ejemplo, la desviación residual es de 129,38, menor que la obtenida con el valor nulo, 242,35.

Esto también puede servir para comparar varios modelos, de forma que se ajustará mejor a los datos aquel que tenga una desviación menor.

Otra utilidad de estos parámetros es que nos permiten calcular un pseudo-R², de significado similar al coeficiente de determinación de la regresión lineal. Podemos calcularlo según la siguiente fórmula:

pseudo-R² = 1 – (desviación del modelo / desviación del modelo nulo)

En nuestro caso, tendría un valor de 1 – (129,38 / 242,35) = 0,46. La interpretación es similar a la que se hace en la regresión lineal: el modelo explica un 46% de la varianza total de la variable dependiente.

2. Los grados de libertad. Como en la regresión lineal, dan información de la cantidad de información disponible que se utiliza para estimar los parámetros del modelo. O sea, nos informan de la complejidad del modelo, que influirá en la bondad de ajuste y la capacidad de generalizar el modelo con otros datos diferentes a los empleados para su elaboración.

Los grados de libertad del modelo nulo se calculan como el número de observaciones menos 1. En nuestro ejemplo, 205 – 1 = 204. Los de nuestro modelo se obtienen restando el número de coeficientes del modelo al número de observaciones: 205 – 7 = 198.

Un número de grados de libertad bajo puede indicar una complejidad excesiva del modelo. Si comparamos varios modelos, en general preferiremos aquellos con más grados de libertad. Recordad que los modelos más complejos son los que tienen más riesgo de realizar sobreajuste de los datos (overfitting).

Por último, los grados de libertad y los valores de las desviaciones nos permiten calcular la significación estadística global del modelo (que es lo mismo que decir que calcular si la diferencia entre nuestro modelo y el modelo nulo es estadísticamente significativa).

Esto es similar al valor de la F que se calcula en la regresión lineal. En el caso de la regresión logística recurrimos a la ji-cuadrado para calcular la llamada ji-cuadrado residual:

ji-cuadrado residual = desviación nula – desviación residual

Este valor, (en nuestro ejemplo, 242,35 – 129,38 = 112,97) sigue una distribución de la ji-cuadrado con un número de grados de libertad que se calculan restando los grados de libertad de la desviación residual de los grados de desviación nula. En nuestro ejemplo serían 204 – 198 = 6. Ya podemos acudir a R y pedirle que calcule el valor de p para este valor de la ji-cuadrdo residual:

1 - pchisq(112.97, 6)

Vemos que el valor de p es prácticamente cero: nuestro modelo es estadísticamente significativo. De todas formas, merece la pena recordar que el hecho de que el modelo sea estadísticamente significativo no quiere decir que se ajuste bien a los datos, sino que, simplemente, es capaz de predecir mejor que el modelo nulo.

En ocasiones, un modelo significativo y con un valor de pseudo-R² bajo (o elevada desviación) nos indicará que, aunque el modelo funciona mejor que el modelo nulo, su capacidad de hacer predicciones (su bondad de ajuste) no es buena. Seguramente haya, en casos similares, más variables implicadas en el comportamiento de los datos y que no hemos incluido en el modelo (aunque también puede ocurrir que el tipo de modelo elegido no es el más adecuado para explicar nuestros datos).

3. El criterio de información de Akaike (AIC). Representa la log-verosimilitud ajustada por el número de coeficientes del modelo. Esto es similar a cómo se ajusta el coeficiente de determinación de la regresión lineal y refleja, de alguna manera, la complejidad del modelo.

El AIC permite comparar varios modelos que empleen diferentes variables predictivas. En general, preferiremos el modelo con el AIC más bajo, ya que probablemente su bondad de ajuste y su capacidad de generalizar su aplicación sea la mejor (menos riesgo de sobreajuste).

4. Número de iteraciones de la puntuación de Fisher (number of Fisher scoring iterations).

Al final del resumen del modelo nos encontramos con el número de iteraciones del algoritmo de Fisher scoring (perdonadme el término en inglés, pero todo el mundo lo llama así).

Dicho de forma sencilla, es un algoritmo que trata de encontrar los estimadores de máxima verosimilitud del modelo. El algoritmo comienza a funcionar y va haciendo iteraciones hasta que los coeficientes del modelo convergen, lo que quiere decir que dejan de observarse cambios sustanciales en los parámetros con nuevas iteraciones, encontrándose así los coeficientes que maximizan la función de verosimilitud.

Lo esperable es que se produzca la convergencia tras 6-8 iteraciones. Cuando el número sea mayor, significará que puede que no haya habido convergencia, lo que resta validez al modelo. En nuestro ejemplo, el número de iteraciones es 5, dentro de lo que se considera adecuado.

El método de Fisher es muy utilizado, pero podéis encontrar también algún otro, como el de Newton-Raphson.

Nos vamos…

Y con esto terminamos esta larga entrada, pero es que la regresión logística tiene mucha miga. En realidad, tanta como poder demostrar que te puedes resfriar o broncear por la acción del aire.

Hemos revisado como valorar el resumen de un modelo de regresión logística, utilizando para ello un conjunto de datos de cuya veracidad no me hago responsable desde el punto de vista médico. Que nadie saque conclusiones sobre el melanoma basándose en estos datos.

Hemos pasado por encima la última parte, la de la convergencia del modelo. ¿Qué pasa cuándo no hay convergencia? ¿Podemos hacer algo para remediar el problema?

Una de las causas puede ser que haya lo que se llama separación o cuasi-separación, que se produce cuando una o varias variables independientes son capaces de predecir muy bien la variable dependiente para un subconjunto de los datos disponibles para elaborar el modelo. Es curioso, pero la regresión logística puede funcionar peor si alguna de las variables es “demasiado buena”.

Aunque no hay que desesperar. Siempre podemos tratar de minimizar el problema recurriendo a las técnicas de regularización de la regresión. Pero esa es otra historia…