Odds ratio.

La odds ratio nos permite calcular la fuerza de la asociación entre exposición y efecto cuando no conocemos los riesgos basales.
¿Os gusta el juego?. Me refiero a los juegos de azar que la gente busca en los casinos con la vana esperanza de ganar un poco (o no tan poco) de dinero a la vez que se divierte. Pero la gente que desea enriquecerse de forma rápida y divertida olvida dos cosas. La primera es que todo lo que ve alrededor (y mucho más que no ve) lo pagan los miles que previamente fracasaron en un intento similar al suyo. La segunda es estudiar antes a fondo cuáles son sus probabilidades de ganar… y sus odds.
Odds y probabilidad
Os preguntaréis qué es una odds y por qué usamos un término tan raro. A la segunda pregunta os diré que no he encontrado una palabra castellana que guste a la mayoría. Quizás las que más me gustan a mí sean “oportunidad relativa” o “probabilidad relativa”, pero para seguir la corriente general, me quedaré con odds. Para contestar a la primera pregunta tenemos que calentarnos un poco las neuronas.
Todos entendemos el concepto de probabilidad. Si nos preguntan cuál es la probabilidad de sacar un seis si tiramos un dado en el casino, responderemos rápidamente que la probabilidad es una entre seis o 1/6 (0,16 ó 16,66%). Pero al jugador quizás le interese más saber cuánto es más probable que salga el seis frente a que no salga. Y la respuesta no es 1/6, sino 1/5.
¿Por qué?: porque la probabilidad de que salga es 1/6 y la de que no salga es 5/6. Para saber cuánto más probable es sacar el seis debemos dividir 1/6 entre 5/6, lo que nos daría 1/5 (20%). Esta es la odds: la probabilidad de que ocurra un suceso respecto a la probabilidad de que no ocurra: odds = p / (1-p), para los amantes de las fórmulas.
Salgamos ahora del casino. He observado que la noche que echo una mirada a las noticias en Internet antes de acostarme duermo peor. Supongamos que hago una encuesta preguntando a la gente que me encuentro por la calle si duermen bien y si acostumbran a ver las noticias antes de acostarse y obtengo los resultados que os muestro en la tabla.
Riesgo relativo y odds ratio
Podemos preguntarnos ¿cuál es la probabilidad de que alguien que lea las noticias sea insomne?. Fácil: 25/79 ó 0,31 (número de lectores insomne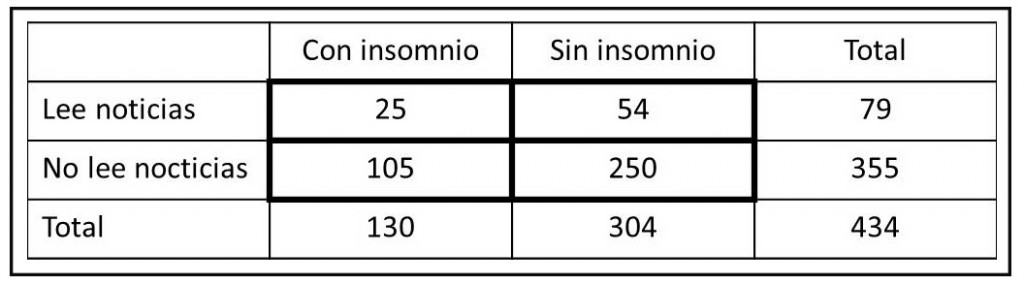
Calculamos igualmente la probabilidad de que un no lector sea insomne como el cociente 105/355 = 0,29 (no lectores insomnes dividido por el total de no lectores). La odds, por su parte, sería de 105/250 = 0,42 (no lectores con insomnio dividido por no lectores sin insomnio).
Si calculamos ahora el cociente de las dos probabilidades obtendremos el riesgo relativo, RR = 0,31/0,29 = 1.06. Esto quiere decir que el riesgo de tener insomnio es más o menos el mismo entre los que leen las noticias y los que no. Si calculamos el cociente de las dos odds obtendremos un valor de 1,09 (0,46/0,42). Esta es la denominada odds ratio (OR), un parámetro bastante interesante que, en breve, veremos para qué sirve.
Vamos ahora a analizar de nuevo los datos de la tabla, pero esta vez al revés. ¿Cuál es la probabilidad de que un insomne lea las noticias?: 25/130 = 0,19. ¿Cuál es la odds del insomne de leer frente a no leer las noticias?: 25/105 = 0,23. ¿Cuál es la probabilidad de que el que no tiene insomnio sea lector?: 54/304 = 0,17. ¿Y su odds?: 54/250 = 0,21.
Si calculamos el RR = 0,19/0,17 = 1,11, nos dirá que los insomnes tienen el mismo riesgo, aproximadamente, de haber leído las noticias antes de acostarse que los que duermen plácidamente. ¿Y la OR?: 0,23/0,58 = 1,09. ¡Pásmate!, la OR es la misma se miren los datos como se miren, lo cual no puede ser casualidad, sino que debe esconder algún significado.
Odds ratio
Y esto es así porque la OR, también llamada razón de predominio, mide la fuerza de la asociación entre el efecto (el insomnio) y la exposición (leer las noticias). Su valor es siempre el mismo aunque cambiemos el orden de las proporciones en la tabla. 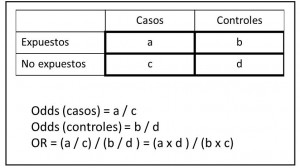
Cuánto mayor sea la OR, mayor será la fuerza de la asociación. Las OR menores de uno son más complejas de interpretar, aunque podemos hacer un razonamiento similar al que hacíamos con los RR menores que uno. Pero aquí acaba la similitud entre los dos. El uso correcto del RR precisa del conocimiento de la incidencia del efecto en las dos poblaciones comparadas mientras que la OR se calcula en base a la frecuencia observada en las dos, por lo que no son parámetros equiparables aunque su interpretación sea similar. Solo tienden a igualarse en los casos en los que el efecto tiene una probabilidad muy baja de presentarse.
Por estos motivos, la OR es la medida de asociación utilizada en estudios de casos y controles y metaanálisis, mientras que los RR son preferible para los estudios de cohortes y los ensayos clínicos.
Nos vamos…
Un par de consideraciones antes de acabar con el tema de la OR. Primera, aunque nos permita comparar la asociación entre dos variables cualitativas (categorizadas como sí o no), no sirve para establecer relaciones de causa-efecto entre las dos. Segunda, tiene gran utilidad porque permite evaluar el efecto de otras variables sobre esta asociación, lo que puede servir para planificar la realización de estudios estadísticos de regresión logística. Pero esa es otra historia…
