La prueba de Egger.

En el siglo XVII, un alquimista llamado Hennig Brand estaba convencido de que podía convertir la orina en oro. Pasó años recolectando grandes cantidades de este líquido y realizando innumerables experimentos en su laboratorio. Tras mucho esfuerzo, se le ocurrió poner la orina en ebullición para retirar el agua y, una vez más, calentar el residuo sólido obtenido y recoger el vapor que salía.

Cuando este vapor se enfrió quedó un material blanco y de aspecto cerúleo, que resultó ser el fósforo, elemento desconocido hasta entonces.

Así, aunque no logró el oro que buscaba, se vio recompensado por otro descubrimiento no menos importante. El alquimista tuvo suerte y, aunque su objetivo inicial estaba basado en una suposición errónea, el proceso le llevó a un descubrimiento significativo. Esta historia curiosa de la alquimia tiene un interesante paralelismo con ciertas herramientas modernas de la ciencia del metanálisis.

Tomemos, por ejemplo, la prueba de Egger. Esta prueba se utiliza en metanálisis para detectar el sesgo de publicación, basándose en la idea no demostrada de que los estudios más pequeños se publican más fácilmente cuando tienden a mostrar efectos más grandes, que pueden llegar a ser significativos, a pesar de su menor precisión.

Conocido como el efecto de los estudios pequeños, esta suposición no está exenta de controversia. Algunos autores creen que esta herramienta es esencial para desenmascarar sesgos ocultos, mientras que otros argumentan que confiar en ella es como seguir una receta alquímica sin un fundamento claramente demostrado y que no siempre podrá ofrecer el oro que promete.

Si seguís leyendo esta entrada, exploraremos los misterios y las realidades de esta prueba y descubriremos si realmente puede convertir el plomo de los datos en el oro de la verdad de la inferencia estadística.

Todo empieza con un embudo

Ya vimos en una entrada anterior cómo el gráfico en embudo, más conocido por su nombre inglés de funnel plot, es la herramienta gráfica más utilizada para valorar la posible existencia de un sesgo de publicación en un metanálisis.

Se basa en el estudio de los efectos pequeños que ya hemos comentado un poco más arriba. Según este efecto, el valor de significación estadística del resultado de un estudio, el valor de p, es uno de los condicionantes más importantes que pueden influir sobre si un estudio llega a publicarse o se queda en un cajón del investigador.

Según esto, los estudios pequeños solo se aceptan para publicar si su resultado es significativo. Como estos estudios pequeños suelen ser menos precisos (por su menor tamaño muestral) y sus intervalos de confianza suelen ser más anchos, solo alcanzarán significación estadística si el efecto que detectan es grande. En caso de efectos pequeños, será más probable que el intervalo de confianza cruce el valor nulo y la p no alcance el deseado valor por debajo de 0,05.

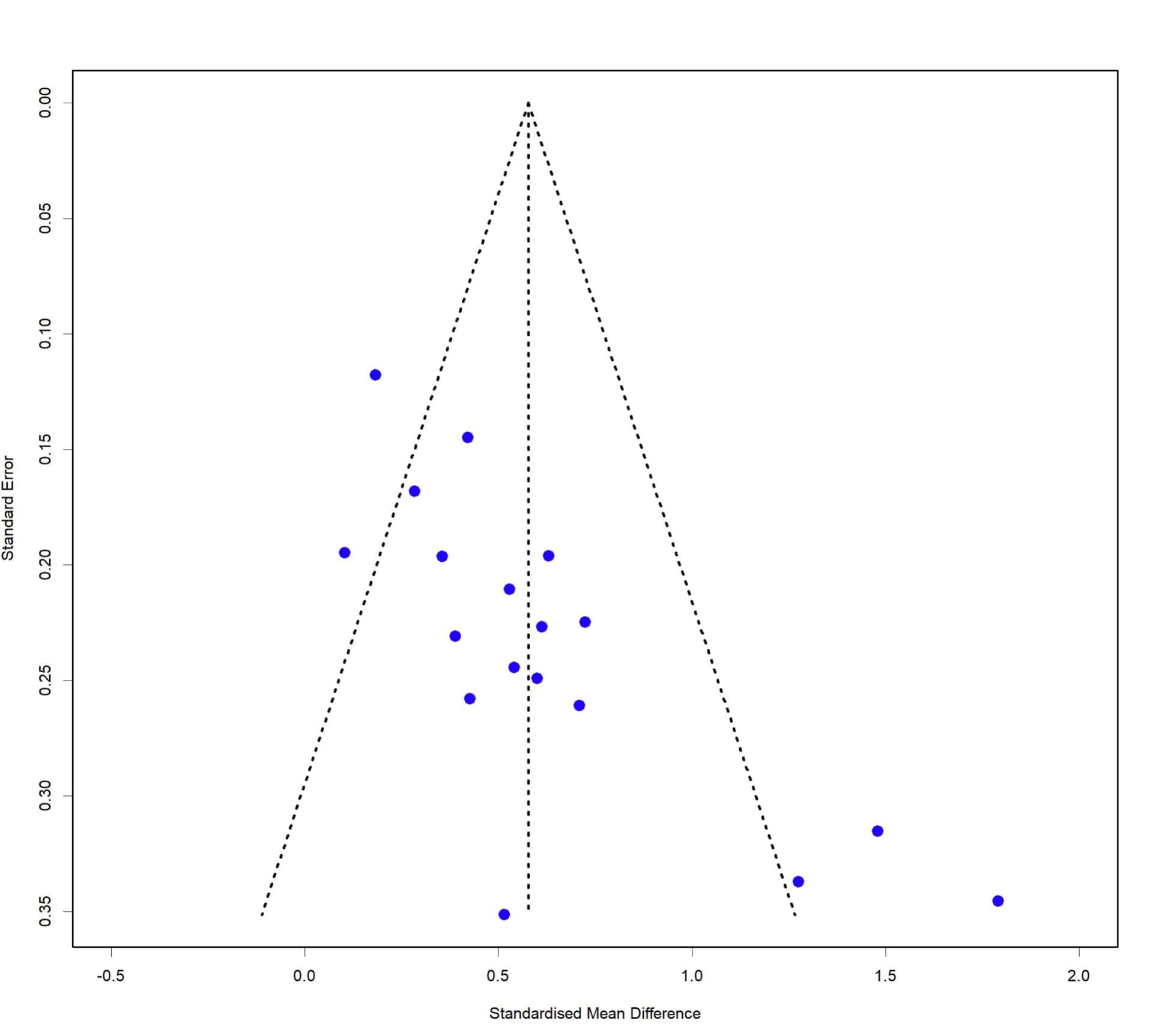
El gráfico en embudo representa la medida de efecto (eje x) frente a una medida de precisión (eje y), que suele ser el inverso del tamaño muestral o el inverso de la varianza o del error estándar. Si representamos cada estudio primario de la revisión, en la zona superior estarán los estudios más precisos, que suelen ser los que tienen tamaño muestral más grande. Al ser más precisos, se agrupan alrededor de la medida resumen con poca dispersión. Podéis verlo en la figura adjunta.

Según nos desplazamos hacia el origen del eje y, los estudios son menos precisos, por lo que se van dispersando de forma más amplia alrededor del valor de la medida resumen del metanálisis.

Si el efecto de los estudios pequeños se cumple, estarán sobrerrepresentados los estudios poco precisos con efectos grandes, generalmente aquellos con resultado favorable a la intervención en estudio. Los no significativos o no favorables tendrán más riesgo de no llegar a publicarse, lo que producirá una asimetría en la distribución de los puntos que representan los estudios del metanálisis.

Esta asimetría nos hará sospechar la existencia de un sesgo de publicación, aunque ya sabemos que puede deberse también a otras razones, como la heterogeneidad entre los estudios primarios.

Así, el gráfico en embudo es una herramienta sencilla y de fácil interpretación para la valoración de este sesgo tan característico de los metanálisis. Sin embargo, el problema que surge es que es un método subjetivo que depende del criterio del que evalúa el gráfico. En algunas situaciones, sobre todo cuando el número de estudios es pequeño, puede ser difícil estimar si existe asimetría o no en el embudo. Necesitamos, pues, métodos para cuantificar de forma objetiva esta asimetría.

Es en estos casos cuando podemos realizar la prueba de Egger.

La prueba de Egger

La prueba de Egger es el método cuantitativo más popular para valorar la asimetría del funnel plot. Se basa en un modelo de regresión lineal entre la medida de efecto y la precisión de los estudios, tal como se muestra en la siguiente ecuación:

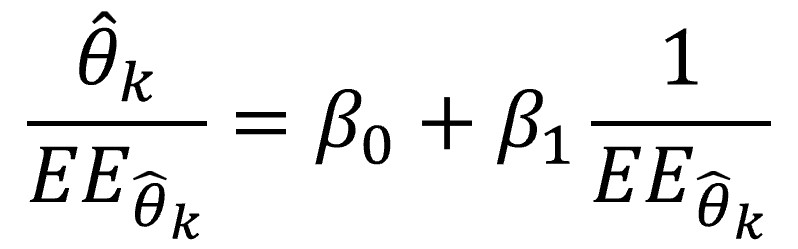
Vamos a pensar un poco qué nos dice la fórmula anterior para, así, poder entender mejor cómo funciona esta prueba.

La variable dependiente o de respuesta es la estimación del valor del efecto del estudio dividida por su error estándar. En realidad, lo que hacemos es estandarizar la medida del efecto, con lo que obtenemos una puntuación z (un z score, para los amantes del inglés).

Utilizar una puntuación z tiene una gran utilidad, ya que podemos saber si el efecto estimado es estadísticamente significativo solo con ver el valor de la puntuación. Como ya sabemos, para una distribución normal y un umbral de significación de p < 0,05, el efecto será significativo si la puntuación z es mayor de +1,96 o menor de -1,96 (para un contraste bilateral).

El modelo de la prueba de Egger regresa esta puntuación z sobre el inverso del error estándar de los estudios, que es equivalente a su precisión (a menor precisión, mayor error estándar).

Pero lo que nos interesa en este caso no es el coeficiente β₁ de la pendiente de la recta, sino el valor de β₀, que debe ser significativamente diferente de cero cuando existe asimetría en el embudo. ¿Por qué? Veámoslo.

Como en cualquier modelo de regresión lineal, β₀ representa el valor de la variable de respuesta cuando todos los predictores valen cero. Como el predictor representa la precisión del estudio, el intercepto representa el valor de z cuando la precisión sea cero (cuando el error estándar sea infinitamente grande).

En ausencia de sesgo de publicación, la magnitud del efecto de los estudios individuales no debe estar correlacionada con su precisión (representada por el inverso del error estándar). En este caso, los efectos de los estudios individuales deben estar distribuidos de manera simétrica alrededor del verdadero efecto resumen (independientemente de su precisión), sin que haya ninguna desviación sistemática de esta distribución.

En términos de regresión, cuando se traza el tamaño del efecto contra su precisión, la línea de mejor ajuste debería pasar por el origen de coordenadas. Es decir, el intercepto de esta regresión debería ser cero, lo que indica que no hay una desviación sistemática de los efectos de los estudios en función de su precisión.

Sin embargo, cuando hay sesgo de publicación, el hecho de que los estudios menos precisos con efecto pequeño no sean publicados provoca una desviación sistemática que favorece a los estudios poco precisos con los efectos más grandes. Esto produce un sesgo del tamaño de efecto respecto a su precisión, con lo que la recta de regresión ya no parte del origen de coordenadas y el intercepto es distinto de cero.

En resumen, un intercepto distinto de cero sugiere que los estudios menos precisos (con mayor error estándar) tienden a estimar tamaños de efecto sistemáticamente diferentes de los estudios más precisos, lo cual es una indicación de sesgo de publicación, donde estudios con resultados no significativos o negativos no se publican con la misma frecuencia que aquellos con resultados positivos y significativos.

Un ejemplo práctico

Veamos cómo se lleva a cabo esta prueba con un ejemplo práctico. Yo voy a utilizar el programa R y el mismo conjunto de datos con los que dibujé el gráfico en embudo que vimos al comienzo de esta entrada.

No os voy a aburrir con los comandos de R, que no son muy complicados, y solo os diré que, tras calcular el modelo de regresión, me proporciona un valor del intercepto de 4,11.

R hace un contraste de hipótesis asumiendo la hipótesis nula de que el intercepto es igual a 0. Obtiene un valor de t = 4,68 con 16 grados de libertad, con lo que calcula un valor de p = 0,0003. Por tanto, al ser p < 0,05, rechazamos la hipótesis nula y asumimos que el intercepto es distinto de cero, lo que indica una asimetría en el gráfico en embudo (probablemente debida a sesgo de publicación).

Podemos representar el modelo de regresión y los estudios primarios, tal como aparecen en la siguiente figura. Como ya sabemos por el contraste numérico, el origen de la recta no pasa por el origen de coordenadas.

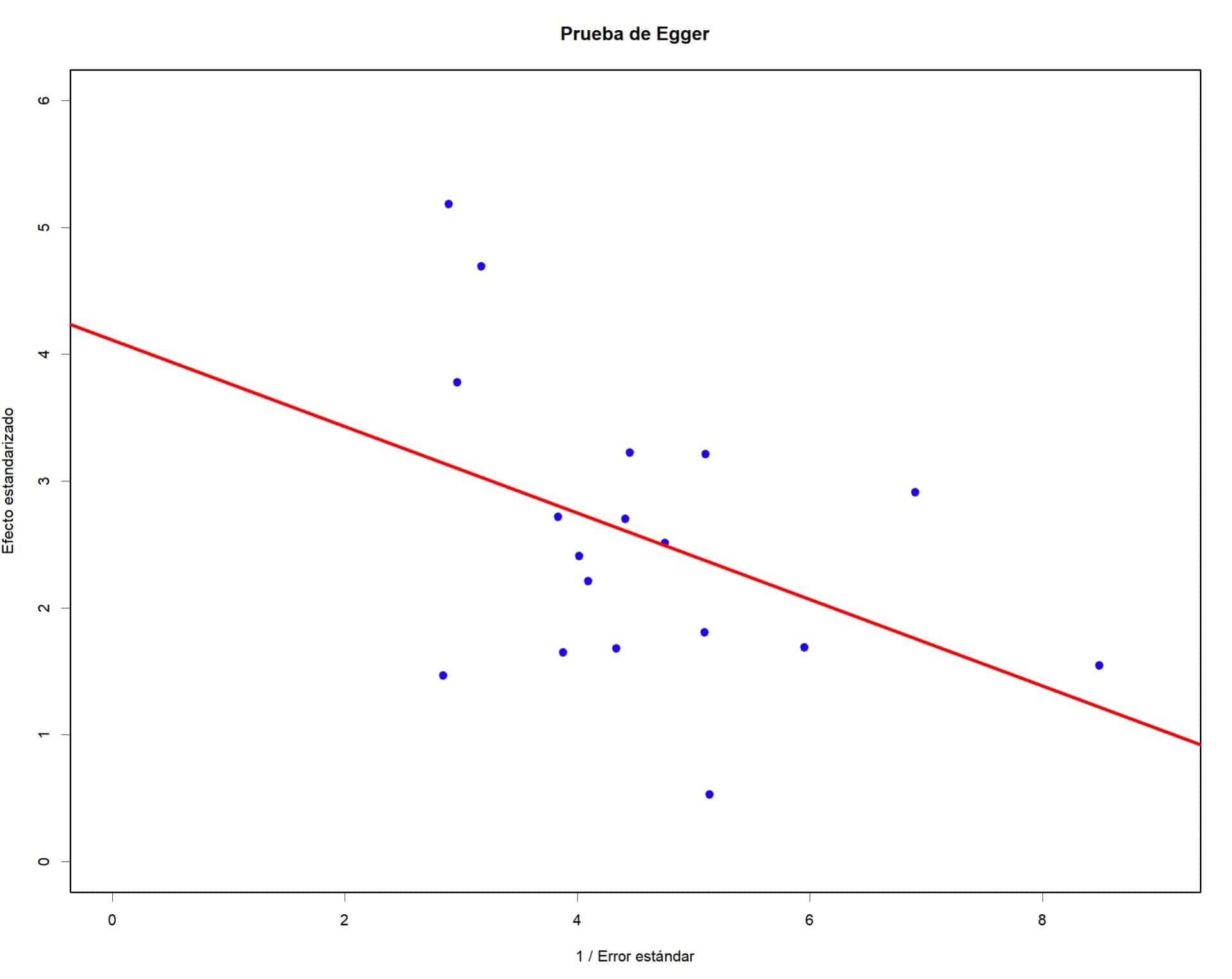
Prueba de Peters

Vimos en el ejemplo anterior cómo se establece la relación entre tamaño de efecto y error estándar para el caso de un metanálisis cuya medida de efecto es una diferencia de medias estandarizada.

Esta dependencia también se da en los metanálisis con resultados con variables binarias (riesgos relativos, odds ratios, etc.). El problema en estos casos es que estas medidas no siguen una distribución normal, por lo que la realización de la prueba de Egger tiene el riesgo de producir un aumento de falsos positivos.

En estos casos podemos recurrir a una variación que se conoce como la prueba de Peters que, también bajo un modelo de efectos aleatorios, establece el modelo de regresión entre el efecto log-transformado (para que se ajuste a una normal) y el inverso del tamaño muestral. Para los amantes de las fórmulas, os la muestro a continuación:

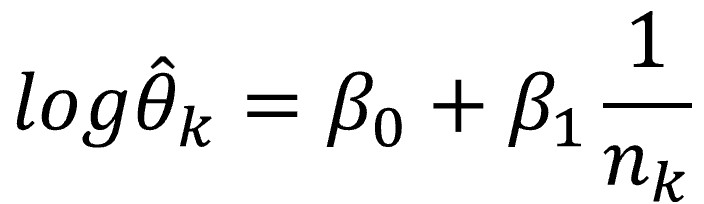
El modelo de regresión de la prueba de Peters es un poco más complejo que el de la prueba de Egger, ya que realiza una regresión ponderada. Esto quiere decir que cada estudio se pondera en función del tamaño muestral y el número de eventos observados y que el modelo se calcula con una modificación del método de los mínimos cuadrados que tiene en cuenta estos pesos.

Esta ponderación asegura que los estudios con mayores tamaños muestrales y más eventos tengan más influencia en determinar la relación entre tamaño del efecto y precisión. No os voy a mostrar más fórmulas, ya que, como suele ser habitual, nadie realiza estos cálculos a mano, sino utilizando paquetes informáticos.

Al igual que ocurría con la prueba de Egger, la de Peters se basa en la relación entre la precisión de los estudios y sus estimaciones del efecto. En ausencia de sesgo de publicación, no se espera que haya una relación sistemática entre el tamaño del efecto y la precisión del estudio (que está inversamente relacionada con el error estándar).

Sin embargo, en presencia de sesgo de publicación, los estudios con menores precisiones (es decir, con mayor error estándar y generalmente con tamaños de muestra más pequeños) tienden a estimar tamaños de efecto más grandes debido a la preferencia por resultados significativos y positivos (están sobrerrepresentados porque tienen más probabilidad de ser publicados).

A diferencia de la prueba de Egger, en la de Peters no nos interesa el intercepto, sino la pendiente de la recta de regresión, el coeficiente β₁: una pendiente significativa (diferente de cero) sugiere una relación entre la precisión y el tamaño del efecto y, por tanto, la presencia de sesgo de publicación.

En particular, una pendiente negativa indicará que los estudios menos precisos (con mayores errores estándar) tienden a estimar tamaños de efecto más grandes, lo cual es, una vez más, indicio de sesgo de publicación.

El procedimiento con un paquete estadístico es similar al que hemos visto con la prueba de Egger, con la diferencia de que esta vez el contraste de hipótesis se hará para la pendiente de la recta de regresión y no para el intercepto.

Regreso a la alquimia

Ya vimos al principio cómo nuestro pobre Hennig Brand fracasó en obtener el oro porque sus métodos se asentaban en teorías no muy bien demostradas, por decir poco.

Pues algo parecido ocurre con la prueba de Egger, como ya hemos comentado con la suposición del efecto debido a los estudios pequeños. Esto hace que haya algunas opiniones que ponen en duda la solidez de la prueba de Egger para la valoración del sesgo de publicación.

En primer lugar, es muy sensible al tamaño muestral. Estudios con tamaños de muestra pequeños pueden generar resultados engañosos, ya que la potencia estadística de la prueba disminuye con muestras pequeñas, lo que podría llevar a una alta tasa de falsos negativos (no detectar un sesgo de publicación existente). En general, tanto la prueba de Egger como la de Peters pueden resultar poco potentes cuando el número de estudios es pequeño, no recomendándose su uso si hay menos de 5 estudios primarios en el metanálisis.

Por si fuera poco, un número de estudios reducido o con unos tamaños muestrales muy diferentes puede poner en riesgo un supuesto necesario para aplicar la prueba: que los errores estándar de los estudios se distribuyan de manera normal.

Además, ya hemos comentado que la prueba de Egger puede dar resultados erróneos cuando existe heterogeneidad alta entre los estudios, confundiendo esta con el sesgo de publicación. Esto puede hacer que aumente el número de falsos positivos cuando existan diferencias metodológicas entre los estudios (claro que, en este caso, puede ser incluso cuestionable la idoneidad de realizar el metanálisis).

Nos vamos…

Y aquí vamos a dejar la alquimia por hoy.

Hemos visto cómo cuantificar la asimetría del gráfico en embudo de una forma más objetiva para tratar de detectar la posible existencia de un sesgo de publicación en un metanálisis. La prueba de Egger es una técnica sencilla de realizar e interpretar, aunque tiene, como hemos visto, algunos inconvenientes, por lo que debe utilizarse con precaución y, si es posible, en combinación con otras técnicas diseñadas para el mismo fin.

Es por eso que se han propuesto algunas alternativas más robustas, como la prueba de Peters que hemos descrito en esta entrada, aunque hay algunas más, tanto gráficas como analíticas.

Una de ellas es la denominada prueba de Egger modificada, que intenta mejorar la robustez frente a la heterogeneidad y disminuir el número de falsos positivos de la prueba. Esto puede realizarse aplicando ponderaciones por el tamaño muestral o transformaciones de los resultados, como la transformación logarítmica. Pero esa es otra historia…