Redes neuronales.

El gran Arthur C. Clarke dijo que cualquier tecnología lo suficientemente avanzada es indistinguible de la magia, sugiriendo que, para alguien que no comprende los principios científicos subyacentes de una tecnología avanzada, esta tecnología puede parecer mágica o incluso milagrosa.

Y es que es una realidad que, a medida que la tecnología avanza, puede ser difícil para el público en general entender cómo funciona, lo que puede llevar a una percepción errónea de la tecnología como algo sobrenatural.

Algo así nos pasa cuando vemos cómo funcionan las redes neuronales. Cuando vemos en acción coches de conducción autónoma, asistentes virtuales o algoritmos de reconocimiento de imágenes, nos parece magia. Pero no nos engañemos, no tienen nada de mágico, sino que están basados en la repetición de operaciones relativamente sencillas.

Lo que sí me parece mágico es el ingenio necesario para desarrollar estas ideas y cómo hacer que la escalabilidad de procesos sencillos reproduzca resultados que, como decía Clarke, nos parezcan mágicos o, incluso, verdaderamente milagrosos.

Vamos a intentar descubrir la ciencia que se esconde detrás de la magia.

Redes neuronales

Las redes neuronales reciben este nombre porque están inspiradas en la estructura y funcionamiento del cerebro humano. De la misma manera que las neuronas son las células básicas del cerebro y están interconectadas en una red compleja, las redes neuronales artificiales están diseñadas con una gran cantidad de unidades de procesamiento interconectadas llamadas, cómo no podía ser de otra forma, neuronas.

Estas neuronas se agrupan en capas que se relacionan entre sí. De forma general, existirá una capa de entrada (donde se introducen los datos que la red procesará), una o varias capas intermedias ocultas o profundas (donde se procesan los datos) y una capa de salida (produce la salida final de la red, que puede ser una clasificación, una predicción o una combinación de ambas).

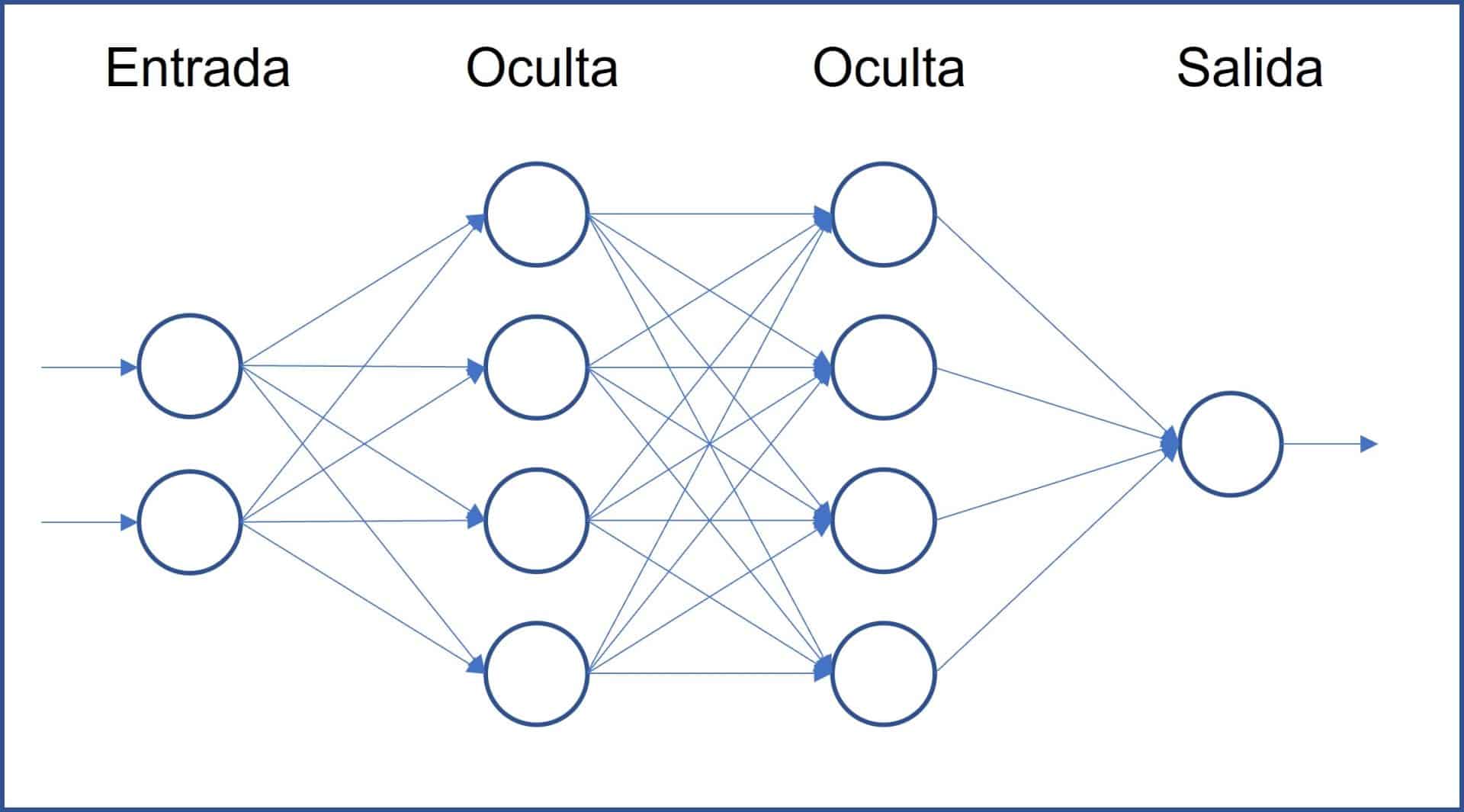
Estas capas se conectan entre sí, de forma que la salida de una capa constituye la entrada de la capa siguiente, como veis en el esquema de la primera figura. Hay varios tipos de redes neuronales que se utilizan para diferentes propósitos, algunos de los más comunes son:

Pero hay algo que todas estas redes tienen en común, y es su unidad básica: la neurona. Veamos cómo funciona.

La neurona

La neurona es el componente fundamental de la red neuronal. Podéis ver en la segunda figura el esquema de funcionamiento de una neurona individual.

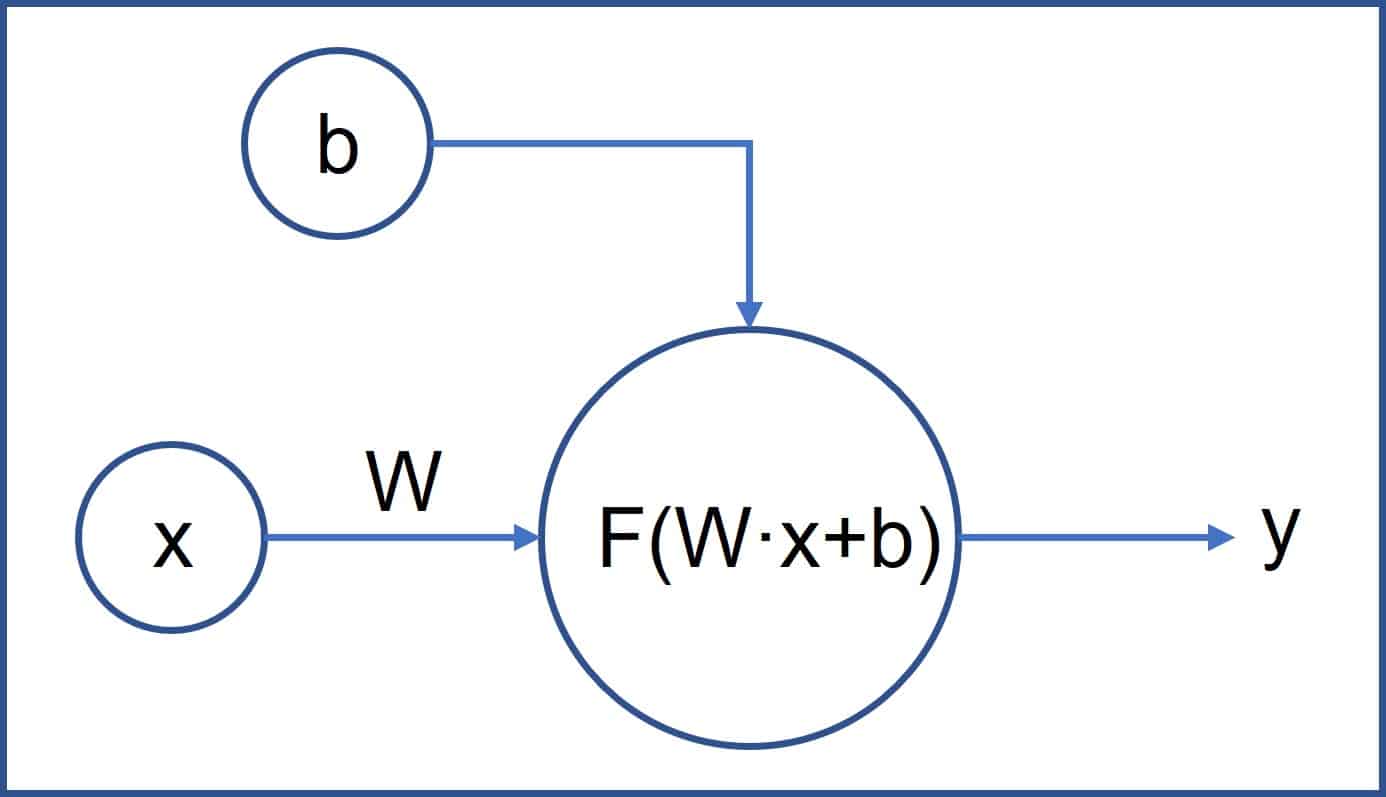
Una neurona recibe una serie de entradas, realiza una operación con ellas y genera una salida, que será la entrada de las neuronas de la siguiente capa (excepto en la última capa, cuya salida es el resultado final que ofrece la red).

Vamos a suponer el ejemplo más sencillo: queremos predecir el valor de una variable “y” en función de otra variable “x”.

La variable x sería una de las entradas de la neurona de la capa de entrada. Pero esta neurona recibe además dos parámetros, uno llamado peso (W, por su inicial en inglés, weight) y otra llamada sesgo (b, por su inicial en inglés, bias).

En el caso de las redes más sencillas, la operación que realiza la neurona es el producto vectorial del peso por la variable, al cual le suma el sesgo:

W · x + b

Lo habitual en la vida real es que haya muchas variables de entrada (x₀, x₁, …, x_n), cada una acompañada de su peso correspondiente (W₀, W_{1, …,} Wn). El punto de la ecuación anterior representa el producto vectorial de las dos matrices (en redes neuronales, las matrices reciben el nombre de tensores). Aquí detrás hay mucha álgebra lineal, pero no necesitamos conocerla a fondo para entender de una forma intuitiva cómo funciona la red.

En el caso de una variable y una red de una neurona, el resultado para predecir el valor de “y” podríamos expresarlo de la forma siguiente:

y = W · x + b

Los más atentos ya habréis pensado que lo que hace la neurona con la variable de entrada no es más que una transformación lineal (la ecuación es similar a la de la regresión lineal simple). El problema es que esta linealidad nos produce un pequeño inconveniente.

Hemos dicho que las redes neuronales están formadas por capas sucesivas de neuronas interconectadas de forma que la salida de una neurona es la entrada de la siguiente. Ahora bien, si todas las neuronas hacen una transformación lineal de su entrada, no nos servirá de nada encadenar capas de neuronas. Y esto es así porque cualquier número de transformaciones lineales sucesivas es equivalente a una sola. No ganaríamos nada encadenando capas de neuronas.

La solución es que cada neurona, una vez realizada la operación anterior, antes de dar la salida, realice una última transformación no lineal. De esto se encarga la denominada función de activación, a la que, en un alarde de creatividad, vamos a llamar f. Así, la ecuación de cada neurona podríamos expresarla del siguiente modo:

salida = f(W · x + b)

Y esta función f ya aplica una transformación no lineal, lo que permite detectar relaciones complejas no lineales entre los datos cuando combinamos varias capas de neuronas.

Hay varias funciones de activación que pueden utilizarse, dependiendo de los datos y del tipo de red utilizada. Para los más curiosos, os diré que la más frecuente es la llamada ReLU (rectified lineal unit, unidad lineal rectificada en la lengua de Cervantes), que deja el resultado como está si es mayor que cero o lo transforma en cero si tiene un valor negativo.

Buscando la magia

Hasta ahora hemos visto qué hace básicamente cada neurona de la red. Hemos puesto un ejemplo sencillo con una variable de entrada, pero en la práctica habrá muchas más: cientos, miles e, incluso, millones de ellas (para complicar más la cosa, también puede haber más de una variable de salida, pero vamos a obviar esto para simplificar).

Vamos a tratar de entender cómo es capaz la red de predecir el valor de salida.

Inicialmente tenemos un modelo de red neuronal con una serie de pesos, según el número de variables de entrada, que se las proporcionaremos nosotros. Además, en nuestro ejemplo sencillo, tenemos que proporcionar a la red el valor de la variable que tiene que predecir. Lo que hace la red es (1) asigna a los pesos un valor inicial aleatorio (sí, un valor al azar), (2) mete los pesos y las variables en la red y hace las operaciones sencillas que cada neurona tiene programadas y, finalmente (3) compara el valor de salida que obtiene con el valor verdadero de “y”, la variable que queremos predecir.

Ya veis, una red neuronal consiste simplemente en una serie de operaciones que hacen unas transformaciones de los datos de entrada para generar un dato de salida. La magia surge cuando se escala el modelo con múltiples neuronas y capas: se convierte en una transformación compleja de los tensores dentro de un espacio multidimensional que ni siquiera somos capaces de imaginar. Eso sí, todo esto se hace a base de una sucesión de pasos sencillos.

Llega el invierno

En el esquema que hemos visto hasta ahora, la red inicializa los pesos aleatoriamente, procesa las variables de entrada y nos da una salida. Como cualquiera puede comprender, cuando comparemos la salida con el valor real de la variable que queremos predecir, lo más probable es que se parezcan poco.

Es lógico, hemos dado un valor aleatorio a los pesos, cuando el objetivo del modelo es calcular (aprender) cuál debe ser el peso que pondere cada variable de entrada para obtener una salida que se parezca lo más posible al valor real.

Esta comparación entre el valor predicho por la red y el real se realiza mediante la llamada función de coste o de pérdida. Por ejemplo, si nuestra red intenta predecir el valor de una variable cuantitativa, la función de coste puede ser la de mínimos cuadrados: compara las diferencias entre predicción y valor real, las eleva al cuadrado (para evitar los signos negativos) y hace la media. También podríamos emplear el valor absoluto de las diferencias. En cualquier caso, necesitamos encontrar el valor de los pesos del modelo que minimice el valor de la función de coste.

Ya solo tenemos que ir modificando los pesos y volviendo a ejecutar el modelo. En un caso real, solo tendremos que modificar a mano miles o millones de parámetros y volver a repetir el proceso para ver cuál es nuestro valor de coste o pérdida.

Esto es, como es fácil de comprender, inviable desde un punto de vista práctico. El objetivo será que la propia red sea capaz de hacerlo de forma automática y aprender qué valores de los pesos son los más adecuados. Por algo se le llama aprendizaje automático.

La falta de una solución para este problema llevó a un periodo de más de 10 años de detención en el avance del desarrollo de las redes neuronales, periodo conocido popularmente como el invierno de la inteligencia artificial.

Pero finalmente llegó la primavera, gracias al desarrollo de dos algoritmos de nombre mágico: retropropagación y gradiente estocástico descendente.

Gradiente estocástico descendente

Ya sabemos que el objetivo de la red es encontrar analíticamente una combinación de pesos que minimice el valor entre la predicción y el valor real. Esto es equivalente a decir que necesitamos encontrar el punto mínimo de la función de coste que estamos empleando, tal como se muestra en la tercera figura.

Pensemos en un modelo con una sola variable como entrada. Su función de coste es continua y diferenciable, lo que significa que podemos calcular la derivada para cualquier valor del peso que hayamos utilizado.

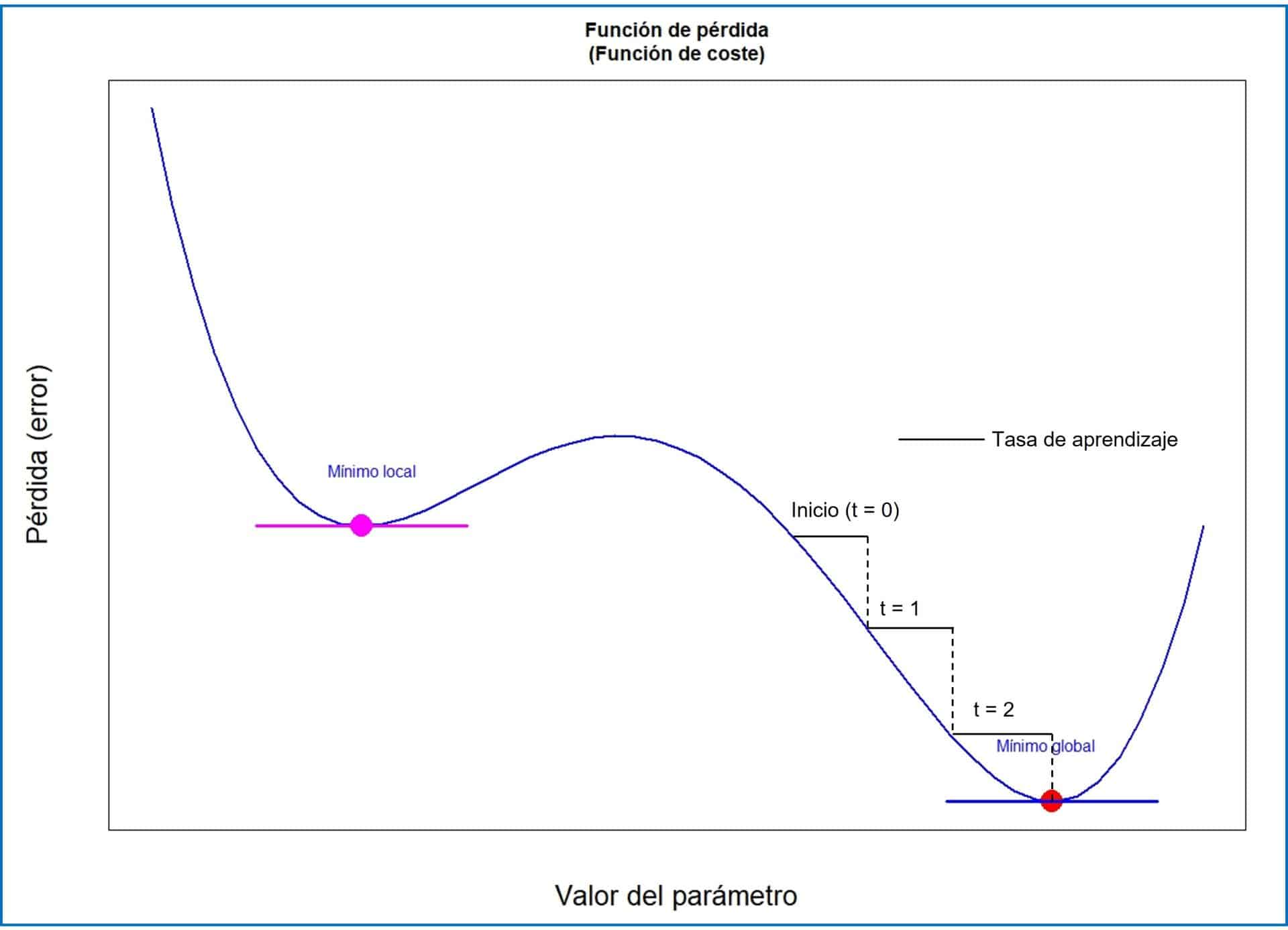
Como sabemos de nuestros tiempos de colegial, la derivada mide la pendiente de la curva de la función. Cuando la derivada aumenta significa que el valor de la función aumenta, y viceversa. En el punto mínimo de la función, la derivada valdrá cero.

Pues ya lo tenemos, solo tenemos que bajar por la curva modificando los pesos del modelo. Para entenderlo mejor, vamos a hacer un paralelismo con un ejemplo de nuestra aventurera vida cotidiana.

Imaginad que os teletransportan hasta un punto en los Alpes y os dicen que tenéis que ir al valle más profundo de la zona. Para hacerlo más sencillo, no conocéis la zona, os tapan los ojos y os dejan en un punto de la cordillera elegido al azar. ¿Cómo encontraréis el valle?

Una forma de hacerlo puede ser la siguiente: dais un par de pasos y tanteáis con el pie hacia dónde va el terreno que tenéis alrededor. Podéis saber así hacia donde baja y hacia donde sube. Cuando ya sabéis hacia donde baja con mayor pendiente, dais otro par de pasos y repetís el proceso. Y así hasta llegar al valle (o hasta acabar despeñados en el fondo de un barranco).

En nuestro modelo de red neuronal, la cordillera es la función de pérdida y nuestro pie es la derivada. En realidad, en un modelo de red neuronal existen numerosas variables de entrada, así que habrá que calcular la derivada parcial que corresponde al peso de cada variable. Con estas derivadas parciales se obtendrá un vector de gradiente, que apunta hacia los valores más altos de la curva. Ya sabemos en qué sentido tenemos que modificar los pesos: en el contrario al que apunta el vector del gradiente.

¿Y en qué cuantía los modificamos? Aquí entraría en juego el equivalente del número de pasos que dábamos en nuestro ejemplo antes de tantear la pendiente. El modelo utiliza un hiperparámetro llamado tasa de aprendizaje, que marca cuánto hay que modificar los pesos (el sentido de la modificación nos lo dará el vector del gradiente).

Una tasa de aprendizaje muy pequeña o muy grande puede hacer que el modelo se estanque y no alcance nunca el mínimo, o que se equivoque y alcance un mínimo local más alto, como el de la figura.

De todos estos cálculos se encarga el optimizador del modelo, que tendremos que especificar cuando diseñemos la red. Hay varios tipos, como RMSprop, Adam, Adamax, gradiente descendente con momento, etc, aunque no vamos a profundizar más en cada uno de ellos.

Retropropagación

Ya hemos solucionado el primer problema para pasar el invierno con el algoritmo del gradiente descendente. Sabemos cómo debemos modificar los pesos del modelo para minimizar la pérdida o coste del mismo, pero necesitamos que la red lo haga y aprenda por sí sola de forma automática. De esto se encarga el algoritmo de retropropagación.

El algoritmo de retropropagación es como el jefe de una empresa que ve de repente que hay una caída en el volumen de ventas de la empresa. Lo que hace es ir departamento por departamento, en el sentido contrario a la cadena de producción, indagando la culpa que tiene cada departamento en el descenso de las ventas y tomando las medidas pertinentes en cada uno de ellos.

De una manera similar, el algoritmo de retropropagación comienza con el valor final de pérdida y trabaja hacia atrás, desde las capas de neuronas más profundas a las más superficiales, calculando la contribución de cada nodo de la red al valor de pérdida de la red. Una vez hecho este cálculo, ajusta los pesos según la tasa de aprendizaje en la dirección contraria al vector de gradiente calculado mediante el algoritmo de gradiente descendente.

Sencillo, ¿verdad? Con todo lo dicho, ya podemos ensamblar todos los componentes para entender cómo funciona una red neuronal sencilla.

Ensamblando la red

En la cuarta figura podéis ver esquematizado el funcionamiento de una red neuronal. Los pasos que sigue la red son los siguientes:

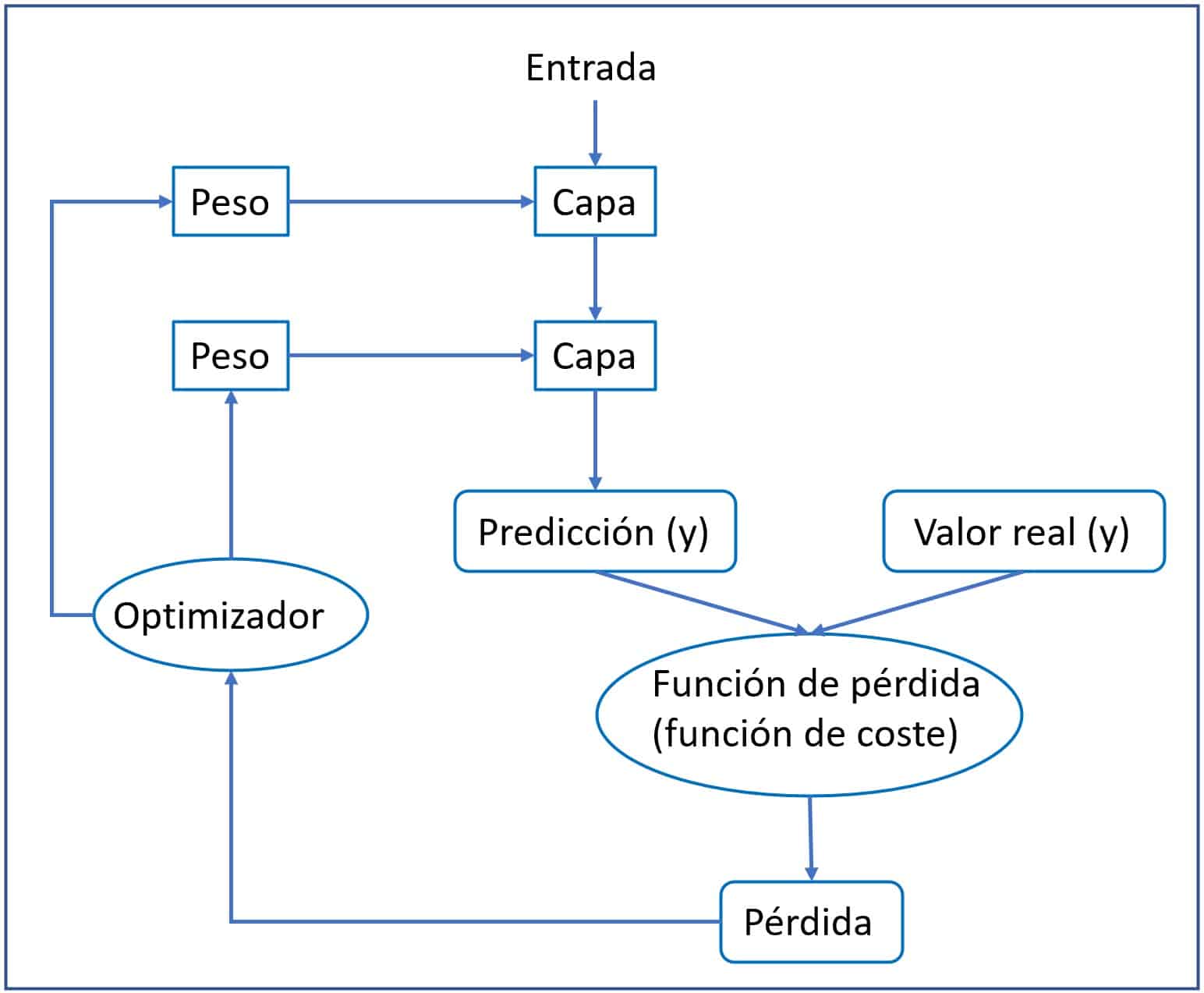
1. Toma un conjunto de variables de entrada (x) y los correspondientes valores reales de la variable que queremos predecir (y).

2. Ejecuta el modelo una vez (paso hacia adelante, forward pass) para obtener las predicciones del modelo de la variable “y”.

3. Calcula la pérdida o coste del modelo, la diferencia entre los valores reales y las predicciones.

4. Se calcula el gradiente de la pérdida en cada nodo en sentido retrógrado (retropropagación).

5. Se modifican los pesos en el sentido opuesto al vector del gradiente (multiplicándolos por la tasa aprendizaje).

6. Se vuelve a ejecutar el modelo con los nuevos pesos, volviendo de nuevo al paso 3 y repitiendo el ciclo el número de veces necesario para que la pérdida o coste del modelo sea mínimo.

Todo este proceso de ensayo y error constituye el entrenamiento de la red, durante el cual aprende cuáles son los valores de los pesos que minimizan el coste del modelo. Cada uno de estos ciclos se denomina época y cada una de estas épocas puede hacerse con todos los datos del modelo o, lo que suele ser más habitual, con porciones de datos que se denominan lotes.

Una vez entrenado el modelo, ya estará listo para predecir el valor de “y” a partir de datos con los que no ha estado en contacto durante la fase de entrenamiento y de los que se desconoce el valor real de la variable.

Nos vamos…

Espero que, con todo lo dicho en esta entrada, hayáis comprendido de forma intuitiva cómo funciona una red neuronal artificial y cómo no tienen nada de magia y sí mucho de ingenio y ciencia matemática.

De todas formas, debo confesaros que a mí me sigue pareciendo algo mágico, aunque entienda un poco la lógica matemática en que se sustentan las redes. Hemos arañado la superficie del funcionamiento de las redes más sencillas. Existen más tipos de conexiones, más tipos de redes y más funciones y técnicas que pueden utilizarse para optimizar el funcionamiento de la red en esa lucha continua entre el entrenamiento excesivo de la red (overfitting) y su aplicabilidad o capacidad de predecir resultados con datos desconocidos. Pero esa es otra historia…