Tamaño muestral en estudios de supervivencia.

A la hora de calcular el tamaño muestral en estudios de supervivencia, el factor determinante no es la diferencia de una medida de efecto entre los dos grupos, sino el número de eventos esperados en cada uno de ellos. Se describe el cálculo del tamaño muestral en estudios de supervivencia en función del número de eventos esperados.
Hoy me vais a perdonar, pero vengo un poco bíblico. Y es que estaba pensando en el cálculo del tamaño de la muestra para los estudios de supervivencia y me ha recordado el mensaje que nos transmite Ezequiel: según tus caminos y tus obras te juzgarán.
Una vez más, pensaréis que de tanto darle vueltas a la medicina basada en la evidencia se me ha ido un poco la cabeza, pero si aguantáis un poco y seguís leyendo, veréis que la analogía tiene su punto.
Una pequeña introducción
Uno de los indicadores de calidad metodológica más valorados de un estudio es el cálculo previo del tamaño muestral necesario para demostrar (o rechazar) la hipótesis de trabajo. Cuando queremos estudiar el efecto de una intervención debemos, a priori, definir qué tamaño de efecto queremos detectar y calcular el tamaño muestral necesario para poder hacerlo, siempre que el efecto exista (algo que deseamos cuando planteamos el experimento, pero que desconocemos a priori), teniendo en cuenta para ello el nivel de significación y la potencia que queramos que tenga el estudio.
En resumen, si detectamos el tamaño de efecto que previamente establecimos, la diferencia entre los dos grupos será estadísticamente significativa (nuestra ansiada p<0,05). Por el contrario, si no hay diferencia significativa, probablemente no exista diferencia real, aunque siempre con el riesgo de cometer un error de tipo 2 que es igual a 1 menos la potencia del estudio.
Hasta aquí parece que está claro, tenemos que calcular el número de participantes que necesitamos. Pero esto no es tan sencillo para los estudios de supervivencia.
El planteamiento del problema
Los estudios de supervivencia agrupan una serie de técnicas estadísticas para aquellas situaciones en las que no basta observar un suceso, sino que es fundamental el tiempo que transcurre hasta que el suceso se produce. En estos casos, la variable de resultado no será ni cuantitativa ni cualitativa, sino de tiempo a suceso. Es una especie de variable mixta que tiene una parte dicotómica (el suceso se produce o no) y una cuantitativa (cuánto tarda en producirse).
El nombre de estudios de supervivencia es un poco engañoso y uno puede pensar que el suceso en estudio será la muerte de los participantes, pero nada más lejos de la realidad. El suceso puede ser cualquier tipo de evento, bueno o malo para el participante. Lo que ocurre es que los primeros estudios se aplicaron a situaciones en los que el suceso de interés era la muerte y el nombre ha prevalecido.
En estos estudios, el periodo de seguimiento de los participantes suele ser desigual e, incluso, algunos pueden terminar el estudio sin presentar el suceso de interés o perderse del estudio antes de que finalice.
Por estos motivos, si queremos saber si hay diferencias entre la presentación del suceso de interés en las dos ramas del estudio, para calcular la muestra no será tan importante el número de sujetos que participen, sino el número de sucesos que necesitamos para que la diferencia sea significativa si se alcanza la diferencia clínicamente importante, que deberemos establecer a priori.
Vamos a ver cómo se hace, dependiendo del tipo de contraste que tengamos pensado utilizar.
Tamaño muestral en estudios de supervivencia
Si solo queremos determinar el número de sucesos necesarios que tenemos que observar para detectar una diferencia entre un grupo determinado y la población de la que procede, la fórmula para hacerlo es la siguiente:
Donde E es el número de sucesos que necesitamos observar, K es el valor determinado por el nivel de confianza y la potencia del estudio y lnTR es el logaritmo natural de la tasa de riesgo.
La tasa de riesgo es el cociente entre el riesgo del grupo en estudio y el riesgo en la población, que se supone que conocemos. Se define como Sm1/Sm2, donde Sm1 es el tiempo medio de aparición del evento en la población y Sm2 el que esperamos en el grupo de estudio.
Vamos a poner un ejemplo para entender mejor lo dicho hasta ahora.
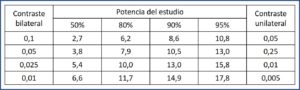
Supongamos que los pacientes que toman un determinado fármaco (que llamaremos A para no esforzarnos mucho) tienen riesgo de desarrollar úlcera de estómago durante el primer año de tratamiento. Ahora seleccionamos un grupo y les damos un tratamiento (B, esta vez) que actúa como profilaxis, de tal forma que esperamos que el evento tarde un año más en producirse. ¿Cuántas úlceras tenemos que observar para un estudio con un nivel de confianza de 0,05 y una potencia de 0,8 (80%)?
K sabemos que vale 7,9. Sm1 = 1 y Sm2 = 2. Sustituimos sus valores en la fórmula que ya conocemos:
Necesitaremos observar 33 úlceras durante el seguimiento. Ahora ya podemos calcular cuántos pacientes tenemos que incluir en el estudio (veo complicado reclutar úlceras).
Vamos a suponer que podemos reclutar 12 pacientes anuales. Si tenemos que observar 33 úlceras, el seguimiento se deberá prolongar durante 33/12 = 2,75, o sea, 3 años. Para más seguridad, planificaríamos un seguimiento un poco superior.
Comparación de curvas de supervivencia
Este es el caso más sencillo. Cuando lo que queremos es comparar las dos curvas de supervivencia (pensamos hacer una prueba de log-rank), el cálculo del tamaño muestral es un pelín más complejo, pero no mucho. Al fin y al cabo, ya estaremos comparando las curvas de probabilidad de supervivencia de los dos grupos.
En estos casos, la fórmula para el cálculo del número de sucesos necesarios es la siguiente:
Nos encontramos un parámetro nuevo, C, que es la relación de participantes entre un grupo y el otro (1:1, 1:2, etc.).
Pero hay otra diferencia con el supuesto anterior. En estos casos la TR se calcula como el cociente de los logaritmos naturales de π1 y π2, que son las proporciones de participantes de cada grupo que presentan el evento en un periodo de tiempo determinado.
Siguiendo el ejemplo anterior, supongamos que conocemos que el riesgo de úlcera en los que toman A es del 50% en los 6 primeros meses y el de los que toman B del 20%. ¿Cuántas úlceras necesitamos observar con el mismo nivel de confianza y la misma potencia del estudio?
Sustituyamos los valores en la fórmula anterior:
Necesitaremos observar 50 úlceras durante el estudio. Ahora necesitamos saber cuántos participantes (no sucesos) necesitamos en cada rama del estudio. Lo podemos obtener con la siguiente fórmula:
Si sustituimos nuestros valores en la ecuación, obtenemos un valor de 29,4, así que necesitaremos 30 pacientes en cada rama del estudio, 60 en total.
Para ir terminando ya, vamos a ver que pasaría si queremos una proporción de participantes diferente de la más fácil, 1:1. En ese caso, el cálculo de n con la última fórmula debe ajustarse teniendo en cuenta esta proporción, que es nuestra conocida C:
Supongamos que queremos una relación 2:1. Sustituimos los valores en la ecuación:
Necesitaríamos 23 participantes en una rama y 46, el doble, en la otra, 69 en total.
Nos vamos…
Y aquí lo dejamos por hoy.
Como siempre, todo lo que hemos dicho en esta entrada es para que podamos comprender los fundamentos del cálculo del tamaño muestral. De todos modos, os aconsejo que, si tenéis que hacerlo alguna vez, utilicéis un programa estadístico o una calculadora de tamaño muestral. Hay muchas disponibles y algunas hasta son totalmente gratis.
Espero que ahora comprendáis lo de Ezequiel: son más importantes las cosas que hacemos (o padecemos) que cuántos las hacemos (o padecemos). Hemos visto la forma más sencilla para calcular el tamaño de la muestra de un estudio de supervivencia. Todavía podríamos complicarnos la vida y calcular el tamaño muestral basándonos en estimaciones de los riesgos relativos o de las tasas de riesgos instantáneos, nuestras queridas hazard ratios. Pero esa es otra historia…
