Tamaño muestral para la estimación de una media.

No cabe duda de que la media, y nos estamos refiriendo a la media aritmética, es la medida de tendencia central más utilizada. Lo que pocos conocen, sin embargo, es su noble origen.

En la actualidad, para que sea más sencillo desde un punto de vista didáctico, decimos que la media aritmética, también llamada promedio, es el resultado que se obtiene sumando todos los valores de una muestra y dividiéndolo por el número de dichos valores.

Pero no siempre fue tan sencillo definir qué es una media aritmética. Hay que remontarse hasta el siglo III antes de Cristo en que un gran genio adelantado a su tiempo, el sabio Arquímedes, se toma en serio el asunto del promedio.

Hasta que el genio con el principio más famoso de la historia se puso a pensar en el tema, el hombre había utilizado el concepto de media aritmética de forma intuitiva. Pero esto cambió.

Arquímedes había usado en muchos de sus trabajos el principio de la balanza para el descubrimiento de propiedades geométricas y lo tomó como un elemento epistemológico fundamental en la construcción de su conocimiento para el cálculo del centro de gravedad, que no es otra cosa que una forma de promedio.

Del uso de la balanza y el centro de gravedad surgen los conceptos de exceso y defecto entre dos cantidades, que tienden a equilibrarse en un punto medio. Y este equilibrio entre el exceso y el defecto es el sustento de nuestra media aritmética.

Viendo el origen tan noble de la media aritmética, no debe resultarnos extraño que esté tan presente en aspectos matemáticos tan fundamentales como son la base del cálculo diferencial o el teorema del límite central.

Pero vamos a dejarnos de historias y vamos a entrar en materia. Hoy vamos a ver qué tamaño muestral necesitamos si queremos estimar la media de una determinada variable en una población utilizando para ello una muestra obtenida de dicha población.

Estimación de una media

Supongamos que queremos hacer un programa de salud en nuestra ciudad para el control de la hipercolesterolemia. Para poder planificar bien nuestro programa, estamos interesados en saber cuál es el valor medio de colesterol sérico en nuestra población.

Lo más exacto sería hacer un análisis a cada uno de los habitantes de la ciudad, sumar los valores de todas las determinaciones y dividir entre el total de muestras analizadas. Este abordaje puede ser conveniente si vivimos en un pueblo con 50 habitantes, pero imaginad que vivimos en Calcuta: tendríamos que hacer más de 14 millones de determinaciones de colesterol, lo que resulta claramente impracticable.

En casos como este, lo que suele hacerse es seleccionar una muestra de individuos que sea representativa de la población diana (los habitantes de la ciudad) y medir la concentración de colesterol sérico en los individuos de la muestra, más accesible.

Una vez que tengamos el valor medio muestral, haremos nuestra estimación del valor que tendrá la media en la población inaccesible, siempre con cierto grado de variabilidad o error, que podemos también determinar.

¿Y cuál es el tamaño muestral necesario para la estimación de una media en una población? La respuesta a esta pregunta depende de una serie de factores que trataremos a continuación.

Factores que influyen en el tamaño muestral para la estimación de una media

Para calcular el tamaño muestral para la estimación de una media debemos establecer, en primer lugar, el nivel de confianza y la precisión que deseamos que tenga nuestra estimación. Además, el tamaño muestral necesario variará según la dispersión de la variable en la población.

El nivel de confianza

Dicho de una forma sencilla, aunque no del todo exacta, el nivel de confianza hace referencia a la probabilidad de que el intervalo de confianza de nuestra estimación incluya el verdadero valor poblacional que no podemos medir directamente.

Lo habitual es elegir una confianza del 95%, con lo que estimaremos un valor puntual con su intervalo de confianza del 95%. Esto se hace utilizando la puntuación estandarizada que deja fuera del intervalo el 5% de la población normal estándar. Este valor es lo que se conoce como Zα, siendo α el nivel de significación (el complementario del nivel de confianza).

Así, si elegimos una confianza del 95%, α valdrá 0,05 y le corresponderá un Z de 1,96 para un contraste bilateral. En la tabla adjunta os muestro algunos de los valores Z más utilizados, aunque pueden calcularse utilizando una distribución normal.

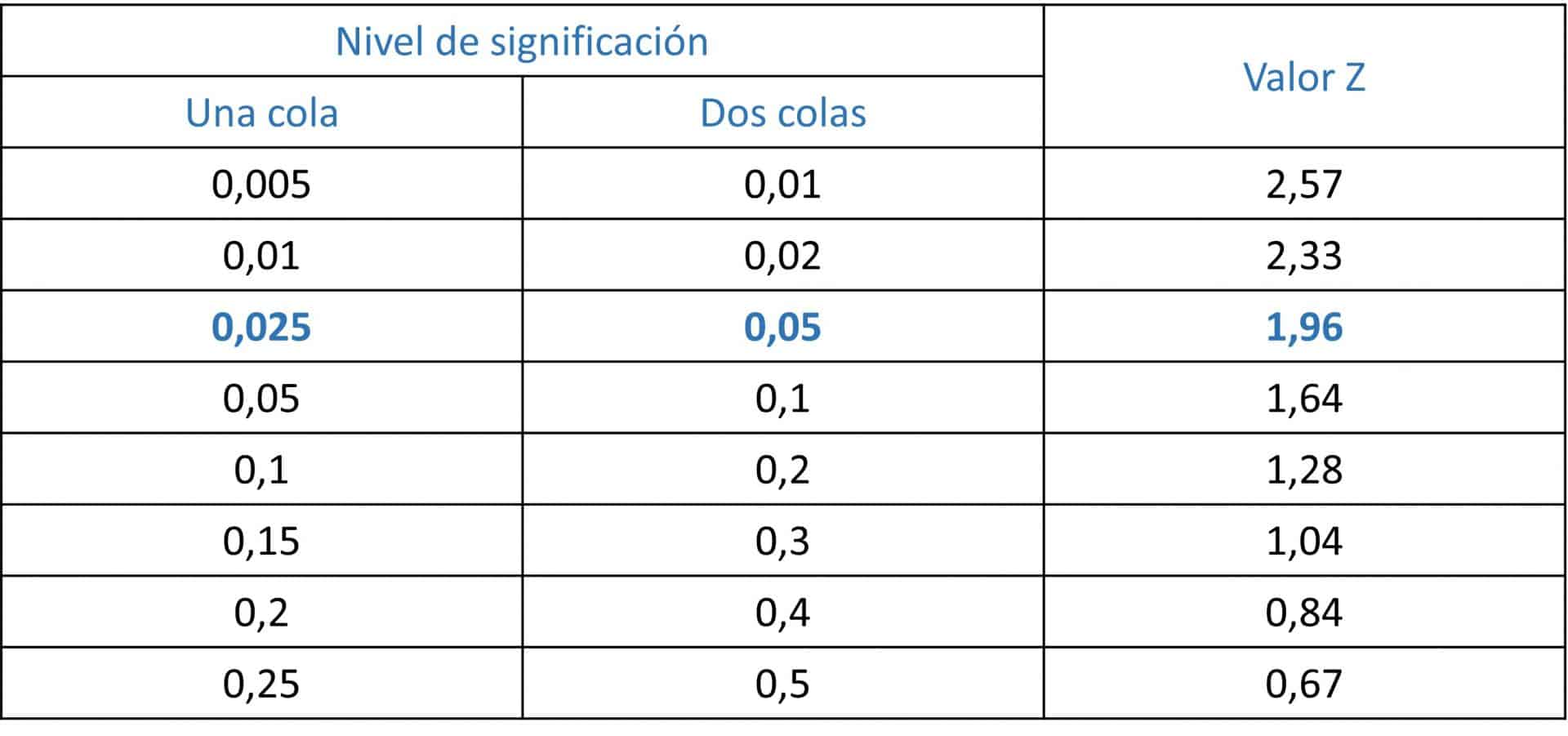
Recordad que esta elección se hace simplemente por convenio y que, según cada caso individual, podemos elegir el nivel de confianza que deseemos. Eso sí, hay que tener en cuenta que el tamaño muestral aumenta de forma directamente proporcional al cuadrado del valor Zα: a mayor nivel de confianza, menor valor de α y mayor Zα, con lo que el tamaño muestral aumentará.

La precisión de la estimación

Como siempre, la precisión se verá reflejada por la amplitud del intervalo de confianza de la estimación.

Lógicamente, querremos hacer una estimación lo más precisa posible, pero hay que tener en cuenta que el tamaño muestral aumenta de forma inversamente proporcional al cuadrado de la amplitud del intervalo. Esto quiere decir que, a menor intervalo, mayor tamaño muestral.

Además, al variar con el cuadrado de la precisión, pequeños aumentos de la precisión de la estimación pueden llevar aparejados un gran aumento de la muestra necesaria para ello.

La dispersión de la variable a estimar

El tamaño muestral necesario es directamente proporcional a la varianza de la variable en la población. Esto quiere decir que, cuanto más dispersos sean los valores de la variable (mayor varianza), mayor será el tamaño muestral necesario para un mismo nivel de confianza y precisión.

Creo que ya podemos ver la fórmula para calcular el tamaño muestral para la estimación de una media, así que os la muestro en la figura adjunta.

Una pequeña corrección

Hasta ahora nos hemos movido en el supuesto de una población diana lo suficientemente grande como para considerarla infinita.

En la práctica, podemos asumir que la población es finita cuando es menor de 5000. En estos casos, una vez calculado el tamaño muestral según la fórmula que ya os indiqué, habrá que hacer la corrección que se indica en la misma figura, de manera similar a como hacíamos al estimar una proporción.

Si no hacemos esto, puede ocurrir incluso que el tamaño muestral necesario que obtengamos sea mayor que la población diana, así que mejor realizar la corrección para población finita y disminuir el tamaño de muestra necesario.

Veamos algún ejemplo

Vamos con nuestro programa de prevención de la hipercolesterolemia. Disponemos de un estudio totalmente ficticio en una población similar a la nuestra en la que la desviación estándar del colesterol es de 20 mg/dl. Ahora queremos estimar la media en nuestra población, con un nivel de confianza del 95% y un intervalo de confianza de ±10 mg/dl.

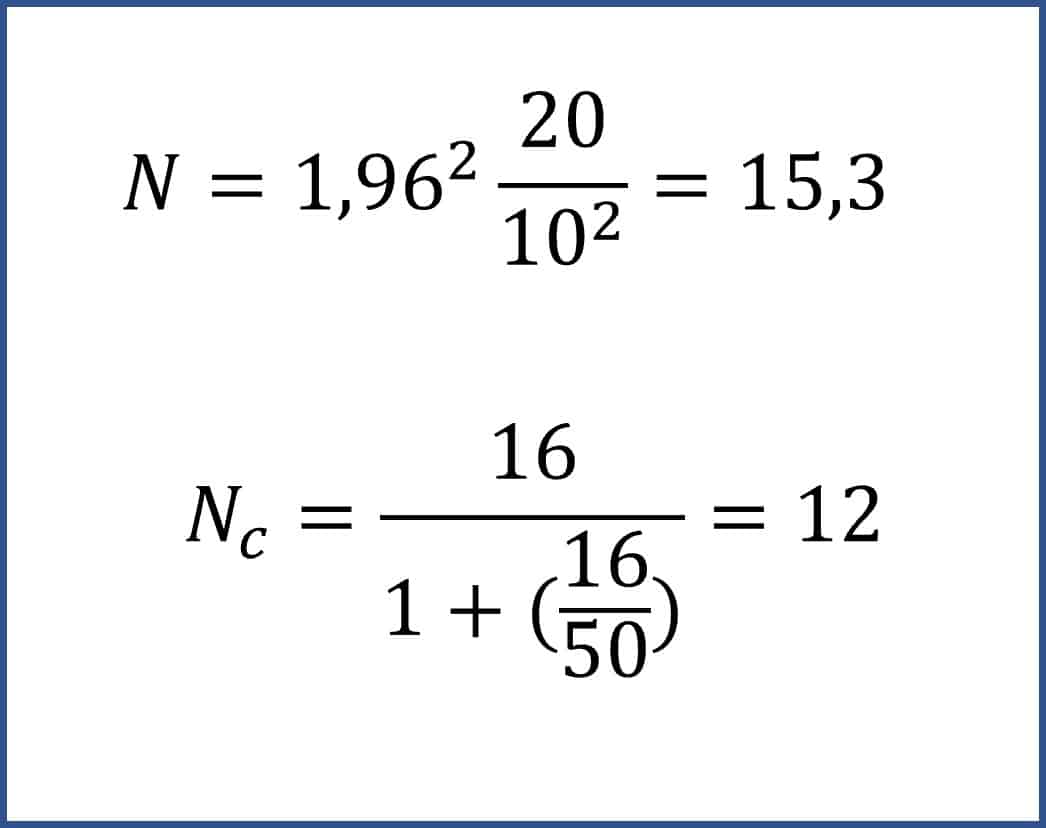
Bien, sabemos que s = 20, Zα = 1,96 y d = 10.

Si sustituimos los valores en la fórmula, tal como se muestra en la figura, veremos que la muestra necesaria es de 15,3 personas, así que podemos redondear a 16.

Ahora vamos a suponer que queremos saber la prevalencia en un grupo de 50 personas y no tenemos dinero para hacerle análisis a todos. Realizamos la corrección para muestra finita según la fórmula que ya conocemos y obtenemos un tamaño muestral corregido algo menor, de solo 12 personas.

Nos vamos…

Y aquí lo dejamos por hoy.

Hemos visto cómo calcular el tamaño muestral necesario para estimar una media poblacional. De todas formas, aunque la fórmula es sencilla, os aconsejo que utilicéis cualquiera de las calculadoras de tamaño muestral disponibles en Internet.

Solo hemos hablado de la media aritmética, que es la que se usa de forma más habitual. Sin embargo, existen variaciones de la media aritmética, muchas de ellas diseñadas para hacerla más robusta frente a la presencia de asimetrías o valores extremos, como la media recortada, la winsorizada y otras. Pero esa es otra historia…