Método de trim-and-fill.

Imaginaos una noche oscura y tormentosa a mediados del siglo XIX. Un grupo de personas se reúne alrededor de una mesa, sosteniendo sus manos, con velas parpadeantes que proyectan sombras danzantes en las paredes. En la penumbra, esperan con ansias una señal del más allá. Este es el mundo del espiritismo, una práctica fascinante y un tanto escalofriante que buscaba comunicarse con los muertos, revelando secretos escondidos y trayendo consuelo (o terror) a los vivos. La popularidad del espiritismo creció como una tormenta, con sesiones que prometían respuestas y fenómenos inexplicables.

Pero, ¿qué pasa cuando los mensajes del más allá no son tan claros? Aquí es donde entra en juego una pizca de escepticismo. Los médiums y sus seguidores a menudo se enfrentaban a la difícil tarea de interpretar mensajes confusos y, a veces, inexistentes. Esta falta de claridad recuerda a un problema en la ciencia moderna: los estudios no publicados en un metanálisis. Así como los espiritistas intentaban llenar los vacíos en sus sesiones, los científicos que realizan metanálisis buscan métodos para predecir y compensar los efectos de los estudios que nunca ven la luz del día.

Al igual que un médium tratando de escuchar un susurro en el viento, los investigadores utilizan herramientas estadísticas para desentrañar el impacto de esos estudios ocultos, como el método de trim-and-fill que vamos a ver hoy. Se trata de encontrar patrones y señales entre el ruido, estimando cómo los resultados ausentes podrían alterar nuestras conclusiones. Así que, la próxima vez que penséis en mesas parlantes y sesiones espirituales, recordad que en el mundo de la ciencia, estamos tratando de invocar nuestro propio tipo de espíritus: los datos que faltan.

Un embudo para gobernarlos a todos

Vimos en una entrada anterior que el sesgo de publicación constituye el talón de Aquiles del metanálisis, una de las herramientas más potentes en la investigación metodológica.

En un mundo ideal, todos los trabajos científicos deberían tener las mismas oportunidades de ser publicados y alcanzar la fama, pero la realidad no es en absoluto así y los trabajos pueden verse discriminados por razones diversas como la ausencia de significación estadística de sus resultados, la poca popularidad del tema que traten, el tener alguien que los apadrine (léase pague) y el idioma en que estén escritos.

El metanálisis es una herramienta muy potente para la investigación, pero es necesario que recoja todos los estudios relevantes que se hayan realizado sobre el tema. La triste realidad es que los estudios con resultados no significativos corren un gran riesgo de no ser publicados, salvo que detecten un efecto de magnitud grande.

El problema es evidente: si los estudios con resultados negativos o con efectos de pequeña magnitud no llegan a ser publicados, las conclusiones del metanálisis estarán sesgadas por basarse únicamente en el análisis de los estudios grandes con resultado positivo.

Una vez dicho esto, se entiende bien que, en la valoración de la calidad metodológica de un metanálisis, sea crucial valorar la posible existencia de sesgo de publicación (en realidad, deberíamos dar por hecho que existe y tratar de estimar su magnitud y cómo puede haber influido en las conclusiones del metanálisis).

Existen varios métodos para valorar la posibilidad de un sesgo de publicación, el más popular de los cuales es el gráfico en embudo, más conocido por su nombre en inglés, funnel-plot.

En este gráfico se representa la magnitud del efecto medido (eje X) frente a una medida de precisión (eje Y), que suele ser el tamaño muestral, pero que puede también ser el inverso de la varianza o el del error estándar. Representamos cada estudio primario con un punto y observamos la nube de dispersión.

En la forma más habitual, con la medida de precisión en el eje Y, observaremos una menor dispersión de los resultados en los estudios de la parte superior del gráfico, con lo que los puntos estarán más juntos en la parte alta del eje y se irán dispersando al acercarnos al origen del eje Y. Es lógico, al disminuir la precisión del estudio, las estimaciones oscilan de forma más amplia y el efecto de los estudios primarios se separa más de la línea de efecto medio.

Esto da lugar a una nube de puntos en forma de embudo, con la parte ancha hacia abajo. Este gráfico debe ser simétrico y, en caso de que no sea así, debemos sospechar siempre un sesgo de publicación, siempre bajo la suposición (que no es más que eso, una suposición) de que los menos precisos, que serán estudios más pequeños, lo tienen más difícil para ser publicados, salvo que el efecto que detecten sea grande.

Ese hueco que observaremos y que será la causa de la asimetría del embudo es el efecto que, desde el más allá, realizan los estudios que no han llegado a ver la luz. Es la hora de que nuestros médiums se comuniquen con ellos para tratar de estimar qué efecto podrían haber tenido sobre nuestras conclusiones si hubiésemos podido incluirlos en el estudio.

Trim-and-fill

En el mundo del espiritismo la cosa se reduce a los tableros de ouija o a juntar las manos y poca cosa más, pero los estadísticos han ideado toda una variedad de métodos para comunicarse con el más allá.

Hoy vamos a ver un método gráfico muy relacionado con el gráfico en embudo, el método de recortar y rellenar, aunque me vais a permitir que utilice el término en inglés, mucho más estiloso: trim-and-fill.

Este método trata de calcular una estimación del efecto corregida por el sesgo que puedan haber introducido los estudios ausentes. La intención es imputar los estudios faltantes e ir incluyéndolos en el gráfico en embudo hasta que desaparezca la asimetría. Una vez conseguido este embudo extendido, recalcularemos la medida de efecto para obtener una estimación que corrija el efecto de los estudios pequeños.

Para conseguir esto, se siguen una serie de pasos:

1. Recorte (trimming). Primero se localizan los estudios que distorsionan la simetría del embudo, se eliminan y se vuelve a calcular la medida de efecto resumen del metanálisis. Lógicamente, para poder hacer esto necesitamos que las oscilaciones del tamaño de los efectos de los estudios se deban solo al azar y no a diferencias en las poblaciones de los estudios. Dicho de forma más sencilla, lo hacemos bajo el supuesto del modelo de efecto fijo, por lo que si hay una heterogeneidad estadística apreciable tendremos que olvidarnos del método y pensar en otra cosa.

2. Pegar (filling). Ahora asumimos que el centro de todos los efectos es el nuevo efecto resumen que hemos calculado en el paso anterior. Alrededor de este nuevo centro, volvemos recuperar los estudios que recortarnos y nos inventamos (imputamos, en realidad) uno nuevo en espejo con cada uno de los recortados.

Por ejemplo, si la medida resumen es una diferencia de medias estandarizada de 0,6 y el estudio que habíamos recortado tenía una de 0,9 (+0,3 a la derecha), cuando lo volvamos a dibujar añadimos un estudio imputado con un efecto de 0,3 (+0,3 a la izquierda).

Una vez que ya hemos representado todos los estudios, incluyendo los que recortamos al principio y sus simétricos en espejo, volvemos a calcular la medida resumen, aplicando un modelo de efectos aleatorios.

Este nuevo efecto resumen es la estimación corregida por el efecto de los estudios faltantes. Los espíritus han hablado y han aportado su pequeña contribución, haciendo más igualitario el mundo del metanálisis. No me diréis que no tiene algo de poético.

Un ejemplo práctico

Como es habitual, vamos a ver un ejemplo práctico de cómo haríamos este procedimiento, con lo que seguro que lo entendemos mejor.

Vamos  a simular un metanálisis con datos ficticios de 19 estudios. La medida de efecto es una diferencia de medias estandarizada, concretamente, una g de Hedges = 0,64. Vamos a fijarnos primero en el funnel plot de la siguiente figura.

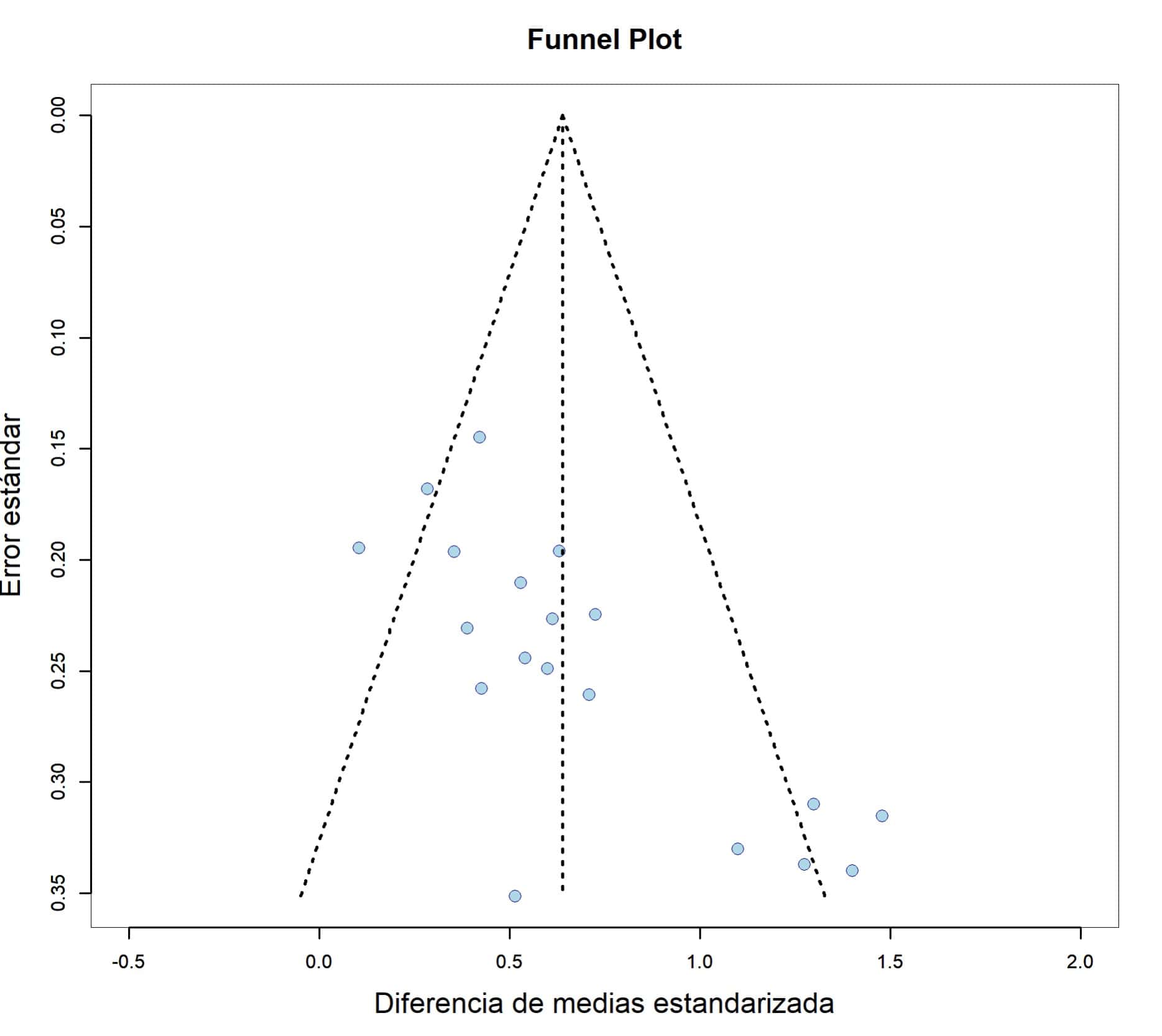
La línea vertical representa el efecto medio estimado, alrededor del cuál se deben colocar estudios primarios. Las otras líneas punteadas que forman un triángulo representan el embudo ideal dentro del cuál se deberían colocar todos los estudios. Como ya sabemos, en la parte alta están los estudios más precisos (menor error estándar), que se agrupan cerca de la línea de efecto medio. Según vamos hacia la parte inferior del gráfico, la precisión disminuye y la dispersión de los resultados aumenta.

Los más despiertos ya os habréis dado cuenta de que el gráfico no es simétrico. Aunque la mayor parte de los estudios están alrededor de la línea de efecto medio, hay un grupo de 5 estudios en el margen inferior derecho que no tiene su representación en el lado contralateral del embudo.

Además, incluso los que están cerca de la línea de efecto medio se encuentran con preferencia hacia el lado de valores de g más bajos.

Esto nos hace sospechar que pueda existir un sesgo de publicación. Además, nuestra estimación puede estar sesgada, ya que el aumento de estudios poco precisos, pero con un efecto de magnitud grande, puede estar sesgando la medida resumen hacia la derecha que, en este caso inventado, vamos a decir que es el extremo favorable a la intervención en estudio.

Estaría bien tratar de estimar cómo la inclusión de los supuestos estudios no publicados puede cambiar la estimación de la medida de efecto global del metanálisis. Vamos a recortar y pegar. Tenéis los dos gráficos en la siguiente figura.

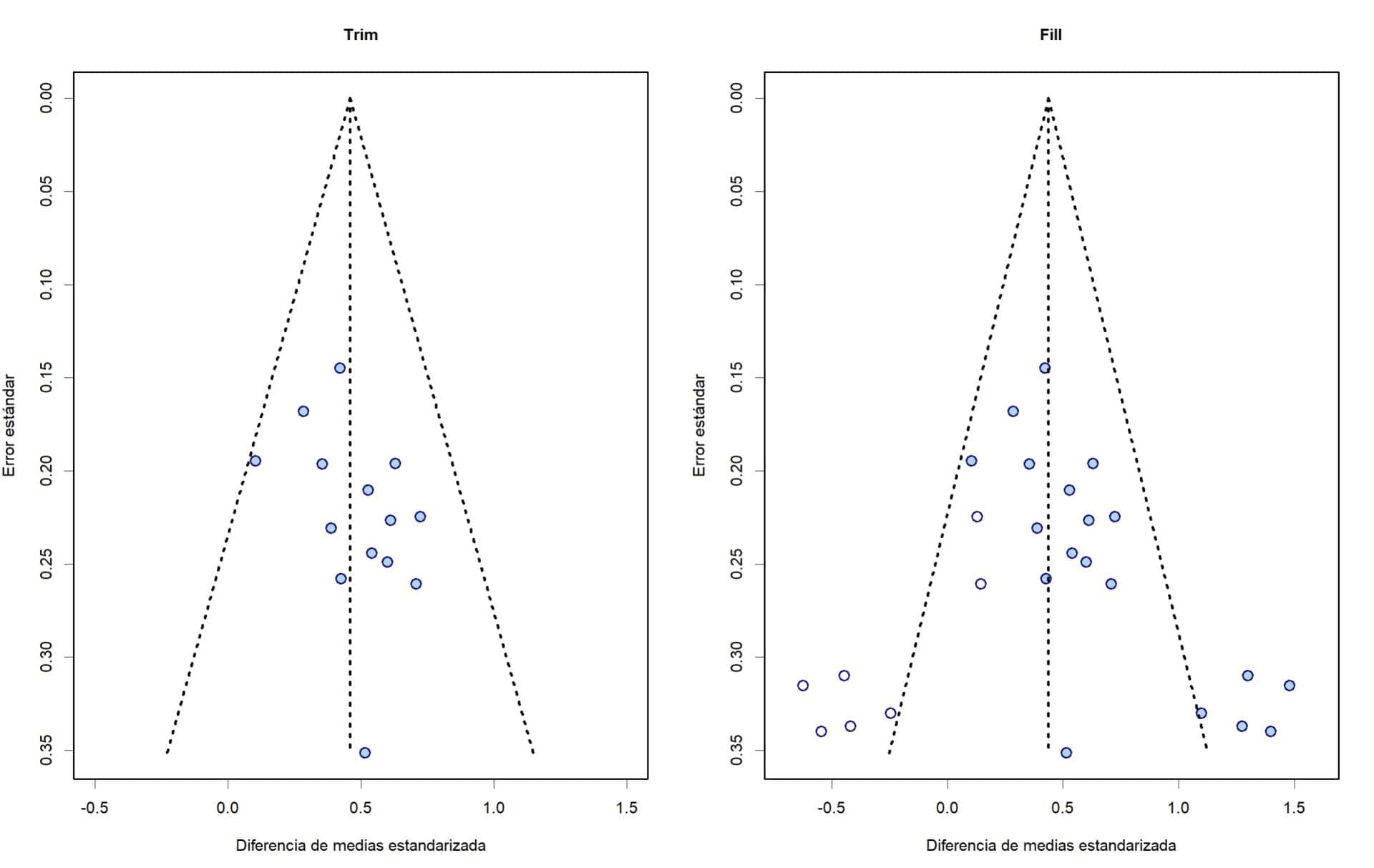
En la primera hemos retirado los 5 estudios del extremo derecho y hemos recalculado tanto la medida de efecto como el nuevo gráfico en embudo. La g de Hegdes nos baja hasta 0,45, lo que ya nos va adelantando que teníamos razón y que los valores extremos de los estudios recortados estaban tirando de la medida de efecto hacia el lado positivo.

Desempolvamos ahora nuestro tablero ouija e invocamos a los estudios del más allá. Esto se hace, como es lógico, utilizando paquetes estadísticos. Yo he utilizado R y sus librerías meta y dmetar.

A la derecha del gráfico podéis ver el funnel plot después de pegar los estudios que supuestamente tendríamos que haber encontrado de no haber sesgo de publicación (son los puntos de color blanco). Vemos que el programa ha calculado que tenía que introducir 7 estudios. Si os fijáis, son la imagen en espejo de los que nos hicieron sospechar.

Ahora el funnel plot es simétrico y, si recalculamos de nuevo la medida de efecto, vemos que nos ha caído hasta 0,43. Sigue habiendo una diferencia significativa, pero la magnitud del efecto es menor de lo que parecía al principio.

Nos vamos…

Y creo que, por hoy, vamos a dejar a los espíritus en paz.

Hemos visto como el funnel plot puede ayudarnos a sospechar la existencia de un sesgo de publicación y como, recortando y pegando, podemos hacer una estimación del efecto real en la población cuando la de nuestro estudio pueda estar sesgada.

De todas formas, este método es fácil de entender, pero tiene algunas limitaciones. Ya hemos dicho que solo puede usarse cuando no haya una heterogeneidad muy alta entre los estudios primarios del metanálisis.

Además, el sesgo de publicación no es la única causa que puede estar detrás de una asimetría del embudo, ya que esta puede deberse también a la presencia de heterogeneidad y de defectos metodológicos en el análisis o recogida de los datos.

Por eso se han desarrollado otras técnicas para abordar este problema, como el llamado método de PET-PEESE. El PET (Precision Effect Test) es, básicamente, una regresión de los efectos estimados por los estudios primarios sobre sus errores estándar, mientras que el PEESE (Precision-Effect Estimate with Standard Error) trata de corregir el sesgo de publicación ajustando el efecto estimado por la precisión del estudio. Pero esa es otra historia…