Valoración de pruebas diagnósticas.

Tengo un cuñado que está muy preocupado con un dilema que le ha surgido. Resulta que va a montar un pequeño comercio y quiere contratar un vigilante para ponerlo en la puerta y que detecte a los que se llevan algo sin pagar. Y el problema es que tiene dos candidatos y no sabe por cuál decidirse. Uno de ellos para a casi todo el mundo, con lo que no se le escapa ningún chorizo.

Eso sí, mucha gente honrada se ofende cuando se le pide que abra el bolso antes de salir y lo mismo la próxima vez se va a comprar a otro sitio. El otro es todo lo contrario: no para a casi nadie pero, eso sí, si para a uno, seguro que lleva algo robado. Este ofende a pocos honrados, pero se le escapan demasiados chorizos. Difícil decisión…

¿Y por qué me viene a mí mi cuñado con este cuento?. Pues porque sabe que yo me enfrento a diario con un dilema similar cada vez que tengo que elegir una prueba diagnóstica. Y es que todavía hay quien piensa que si tú pides una prueba y es positiva ya tienes hecho el diagnóstico y, al revés, que, si estás enfermo, para saberlo no hay más que hacerte la prueba. Y las cosas no son, ni muchos menos, tan sencillas, ni es oro todo lo que reluce, ni todo el oro tiene los mismos quilates.

Valoración de pruebas diagnósticas

Veámoslo con un ejemplo. Cuando queremos saber el valor de una prueba diagnóstica, habitualmente comparamos sus resultados con los de un patrón de referencia o patrón oro (el gold standard de los que saben inglés), que es una prueba que, idealmente, es siempre positiva en los enfermos y negativa en los sanos.

Ahora supongamos que yo hago un estudio en mi consulta del hospital con una prueba diagnóstica nueva para detectar una determinada enfermedad y obtengo los resultados de la tabla adjunta (los enfermos son los que tienen la prueba de referencia positiva y los sanos, negativa).

Sensibilidad y especificidad

Empecemos por lo fácil. Tenemos 1598 sujetos, 520 de ellos enfermos y 1078 sanos. La prueba nos da 446 positivos, 428 verdaderos (VP) y 18 falsos (FP). Además, nos da 1152 negativos, 1060 verdaderos (VN) y 92 falsos (FN). Lo primero que podemos determinar es la capacidad de la prueba para distinguir entre sanos y enfermos, lo que me da pie para introducir los dos primeros conceptos: sensibilidad (S) y especificidad (E).

La S es la probabilidad de que la prueba clasifique correctamente a los enfermos o, dicho de otro modo, la probabilidad de que el enfermo sea positivo. Se calcula dividiendo los VP por el número de enfermos. En nuestro caso es de 0,82 (voy a emplear tantos por uno, pero si a alguien le gustan más los porcentajes ya sabe: a multiplicar por 100).

Por otra parte, la E es la probabilidad de que se clasifique correctamente a los sanos o, dicho de otro modo, de que los sanos tengan un resultado negativo. Se calcula dividiendo los VN entre el número de sanos. En nuestro ejemplo 0,98.

Alguien podrá pensar que ya tenemos medido el valor de la nueva prueba, pero no hemos hecho nada más que empezar. Y esto es así porque S y E nos miden de alguna manera la capacidad de la prueba para discriminar sanos de enfermos, pero nosotros lo que en realidad necesitamos saber es la probabilidad de que un positivo sea enfermo y de que un negativo sea sano y, aunque puedan parecer conceptos similares, en realidad son bien diferentes.

Valor predictivo

La posibilidad de que un positivo sea enfermo se conoce como valor predictivo positivo (VPP) y se calcula dividiendo el número de enfermos con prueba positiva entre el número total de positivos. En nuestro caso es de 0,96. Esto sí quiere decir que un positivo tiene un 96% de probabilidad de estar enfermo.

Por otra parte, la probabilidad de que un negativo sea sano se expresa mediante el valor predictivo negativo (VPN), que es el cociente de sanos con resultado negativo entre el número total de negativos. En nuestro ejemplo vale 0,92 (un negativo tiene una probabilidad del 92% de estar sano).

Y ahora es cuando las neuronas empiezan a recalentarse. Resulta que S y E son dos características intrínsecas de la prueba diagnóstica. Los resultados serán los mismos siempre que hagamos la prueba en unas condiciones similares, con independencia de a quién se la hagamos.

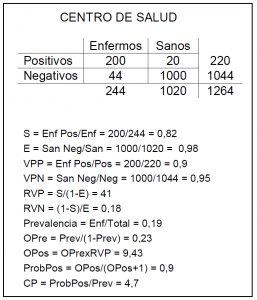
Pero esto no es así con los valores predictivos, que varían según la prevalencia de la enfermedad en la población en la que hacemos la prueba. Esto quiere decir que la probabilidad de que un positivo esté enfermo depende de lo frecuente o rara que sea la enfermedad en su población. Sí, sí, habéis leído bien: la misma prueba positiva expresa diferente riesgo de estar enfermo, y, para los incrédulos, os pongo otro ejemplo. Supongamos que esta misma prueba la hace un coleguilla mío en su consulta del Centro de Salud, donde la población es proporcionalmente más sana (esto es lógico, todavía no han pasado por el hospital).

Si veis los resultados de la tabla, y os molestáis en calcular, veréis que obtiene una S de 0,82 y una E de 0,98, lo mismo que me salía a mí en mi consulta. Sin embargo, si calculáis los valores predictivos, veréis que el VPP es de 0,9 y el VPN de 0,95. Y esto es así porque las prevalencias de la enfermedad (enfermos/totales) son distintas en las dos poblaciones: 0,32 en mi consulta de hospital y 0,19 en la suya.

O sea, que en los casos de prevalencia más alta un positivo ayuda más para confirmar la enfermedad y un negativo ayuda menos para descartarla. Y al revés, si la enfermedad es muy rara un negativo permitirá descartar la enfermedad con una seguridad razonable, pero un positivo nos ayudará mucho menos a la hora de confirmarla.

Vemos pues que, como pasa casi siempre en medicina, nos movemos en el poco firme terreno de las probabilidades, ya que todas (absolutamente todas) las pruebas diagnósticas son imperfectas y cometen errores a la hora de clasificar sanos y enfermos.

Entonces, ¿cuándo merece la pena utilizar una prueba determinada?. Pues si pensamos que un determinado sujeto tiene ya una probabilidad de estar enfermo antes de hacerle la prueba (la prevalencia de la enfermedad en su población), solo nos interesará utilizar pruebas que aumenten esa probabilidad lo suficiente como para justificar el inicio del tratamiento pertinente (en otro caso tendríamos que hacer otra prueba hasta alcanzar el nivel umbral de probabilidad que justifique el tratamiento).

Razón de verosimilitud (cociente de probabilidad)

Y aquí es donde el tema se empieza a poner antipático. La razón de verosimilitud positiva (RVP) o cociente de probabilidad positivo nos indica cuánto más probable es tener un positivo en un enfermo que en un sano.

La proporción de positivos en los enfermos es la S. La proporción de los positivos en sanos son los FP, que serían aquellos sanos que no dan negativo o, lo que es lo mismo, 1-E. Así, la RVP = S / (1-E). En nuestro caso (del hospital) vale 41 (el mismo aunque utilicemos porcentajes para S y E). Esto puede interpretarse como que es 41 veces más probable encontrar un resultado positivo en un enfermo que en un sano.

Puede calcularse también la RVN (la negativa), que expresa cuánto más probable es encontrar un negativo en un enfermo que en un sano. Los enfermos negativos son aquellos que no dan positivo (1-S) y los sanos negativos son los VN (la E de la prueba). Luego la RVN = (1-S)/E. En nuestro ejemplo 0,18.

Un cociente de probabilidad igual a 1 indica que el resultado de la prueba no modifica la probabilidad de estar enfermo. Si es mayor que 1 aumenta esta probabilidad y, si es menor, la disminuye.

Este parámetro es el que usamos para determinar la potencia diagnóstica de la prueba. Valores  >10 (ó <0,1) indican que se trata de una prueba muy potente que apoya (o contradice) fuertemente el diagnóstico; de 5-10 (ó de 0,1-0,2) indican poca potencia de la prueba para apoyar (o descartar) el diagnóstico; de 2-5 (ó de 0,2-0,5) indican que la aportación de la prueba es dudosa; y, por último, de 1-2 (ó de 0,5-1) indican que la prueba no tiene utilidad diagnóstica.

Probabilidad postprueba

La razón de verosimilitud (likelyhood ratio para los ingleses) no expresa una probabilidad directa, pero nos sirve para calcular las probabilidades de ser enfermo antes y después de dar positivo en la prueba diagnóstica. Podemos calcular la odds preprueba (OPre) como la prevalencia dividida por su complementario (cuánto más probable es que esté enfermo a que no lo esté).

En nuestro caso valdría 0,47. Por otro lado, la odds posprueba (OPos) se calcula como el producto RVPxOPre. En nuestro caso, 19,27. Y por último, siguiendo el mecanismo inverso al usado para obtener la OPre a partir de la prevalencia, la probabilidad posprueba (PrPos) sería igual a OPos/(OPos+1). En nuestro ejemplo vale 0,95, lo que quiere decir que si nuestra prueba es positiva la probabilidad de estar enfermo pasa de 0,32 (la prevalencia o probabilidad preprueba) a 0,95 (probabilidad posprueba).

Si todavía queda alguien leyendo a estas alturas, le diré que no hace falta saberse todo este galimatías de fórmulas. Existen en Internet múltiples páginas con calculadoras para obtener todos estos parámetros a partir de la tabla 2×2 inicial con un esfuerzo miserable.

Además, la probabilidad postprueba puede calcularse de forma sencilla utilizando el nomograma de Fagan. Lo que tenemos que saber es cómo valorar adecuadamente la información que nos proporciona una prueba diagnóstica para saber si debemos indicarla en razón de su potencia, costes, molestias para el paciente, etc.

Nos vamos…

Una última cuestión. Llevamos hablando todo el rato de pruebas positivas o negativas, pero cuando el resultado es cuantitativo debemos ser nosotros los que fijemos qué valor consideramos positivo y cuál negativo, con lo que variarán todos los parámetros que hemos visto en esta entrada, sobre todo la S y la E. ¿Y a cuál de las características de la prueba diagnóstica debemos dar prioridad?. Pues eso dependerá de las características de la prueba y del uso que pretendamos darle, pero esa es otra historia…