Variable de confusión.

La variable de confusión está asociada con la exposición y con el efecto sin formar parte de la cadena de causa-efecto entre ambas.

¡Cómo me gustaría tener una máquina del tiempo!. Pensadlo un momento. No tendríamos que trabajar (habríamos ganado la lotería varias veces), podríamos anticiparnos a todas nuestras desgracias, tomar siempre la mejor decisión… Sería como en la película de “El día de la marmota”, pero sin hacer tanto el panoli.

Resultados contrafactuales

Claro que si tuviésemos una máquina del tiempo que funcionase, habría profesiones que podrían desaparecer. Por ejemplo, los epidemiólogos lo llevarían crudo. Si quisiéramos saber, imaginemos, si el tabaco es un factor de riesgo para tener enfermedad coronaria, solo tendríamos que tomar un grupo de personas, decirles que no fumasen y ver qué pasaba veinte años después. Entonces haríamos retroceder el tiempo, les obligaríamos a fumar, veríamos que pasaba veinte años después y compararíamos los dos resultados. ¡Qué fácil!, ¿no?. ¿Quién necesitaría un epidemiólogo y toda su compleja ciencia de asociaciones y diseños de estudios?. Podríamos estudiar la influencia de la exposición (el tabaco) sobre el efecto (la enfermedad coronaria) comparando estos dos resultados potenciales, también llamados resultados contrafactuales (perdón por el palabro).

Sin embargo, a falta de máquina del tiempo, la realidad es que no podemos medir los dos resultados en una misma persona y, aunque parezca una obviedad, lo que quiere decir, en realidad, es que no podemos medir de forma directa el efecto de la exposición en una persona determinada.

Por eso los epidemiólogos recurren al estudio de poblaciones. Normalmente en una población habrá sujetos expuestos y no expuestos, así que podemos tratar de estimar el efecto contrafactual de cada grupo para calcular cuál sería el efecto medio de la exposición sobre la población en conjunto. Por ejemplo, la incidencia de enfermedad coronaria en no fumadores puede servirnos para estimar cuál habría sido la incidencia de enfermedad en los fumadores si no hubiesen fumado. Esto posibilita que la diferencia de enfermedad entre los dos grupos (la diferencia entre sus resultados factuales), expresada mediante la medida de asociación que corresponda, sea un estimador del efecto medio de fumar sobre la incidencia de enfermedad coronaria en la población.

Todo esto que hemos dicho exige un requisito previo: que los resultados contrafactuales sean intercambiables. Esto quiere decir, en nuestro caso, que la incidencia de enfermedad de los fumadores, si no hubiesen fumado, hubiese sido la misma que la que tienen los no fumadores, que no han fumado nunca. Y viceversa: si el grupo de no fumadores hubiese fumado tendría la incidencia que ahora observamos en los fumadores. Esto parece otra obviedad, pero no siempre es así, ya que en estas relaciones entre factor y exposición existen, con frecuencia, puertas traseras que hacen que los resultados contrafactuales de los dos grupos no sean intercambiables, por lo que las estimaciones de las medidas de asociación pueden no ser las correctas. Esto es lo que llamamos factores o variables de confusión.

Variable de confusión

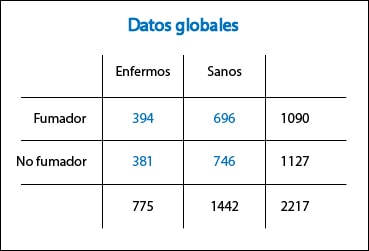
Vamos a aclararnos un poco con un ejemplo ficticio. En la primera tabla os presento los resultados de un estudio de cohortes (que me acabo de inventar) que evalúa los efectos del tabaquismo sobre la incidencia de enfermedad coronaria. El riesgo de enfermar es de 0,36 (394/1090) entre los fumadores y de 0,34 (381/1127) entre los no fumadores, así que el riesgo relativo (RR, la medida de asociación pertinente en este caso) es de 0,36/0,34 = 1,05. ¡Lo sabía!. ¡Si ya lo dijo Woody Allen en “El dormilón”!. El tabaco no es tan malo como se pensaba. Mañana mismo vuelvo a fumar.

¿Seguro?. Resulta que, dándole vueltas al asunto, se me ocurre que igual hay algo que puede estar mal. La muestra es grande, así que es poco probable que el azar me haya jugado una mala jugada. El estudio no tiene, aparentemente, riesgo importante de sesgos, aunque nunca te puedes fiar completamente. Así que, dando por supuesto que Woody Allen se equivocaba en su película, solo queda la posibilidad de que se nos haya metido una variable confusora que nos esté alterando los resultados.

Requisitos de una variable de confusión

La variable confusora tiene que cumplir tres requisitos. Primero, debe estar asociada con la exposición. Segunda, debe estar asociada con el efecto de forma independiente a la exposición que estemos estudiando. Tercero, no debe formar parte de la cadena de causa-efecto entre la exposición y el efecto.

Aquí es donde entra en juego la imaginación del investigador, que tiene que pensar qué variables pueden actuar como confusoras. A mí, en este caso, la primera que se me ocurre es la edad. Cumple el segundo punto (los más viejos tienen más riesgo de enfermedad coronaria) y el tercero (por muy malo que sea el tabaco, no te aumenta el riesgo de enfermar porque te haga más viejo). Pero, ¿satisface el primero?. ¿Hay una asociación entre edad y el hecho de fumar?. Resulta que no lo habíamos pensado antes, pero si esto fuese así, podría explicarlo todo. Por ejemplo, si los fumadores fuesen más jóvenes, el efecto perjudicial del tabaco podría verse contrarrestado por el “beneficioso” de la edad. Y viceversa, el beneficio de los más mayores por no fumar se esfumaría por culpa del mayor riesgo de la edad.

Estratificación

¿Cómo podemos comprobar este punto?. Vamos a separar los datos de los menores y mayores de 50 años y vamos a calcular de nuevo los riesgos. Si los riesgos relativos son diferentes, probablemente querrá decir que la edad está actuando como variable confusora. Por el contrario, si son iguales no habrá más remedio que darle la razón a Woody Allen.

Veamos la tabla de los más jóvenes. El riesgo de enfermar es de 0,28 (166/591) en los fumadores y de 0,11 (68/605) en los no fumadores, luego el RR es de 2,5. Por su parte, en los mayores de 50 años, el riesgo de enfermar es de 0,58 (227/387) en los fumadores y de 0,49 (314/634) en los no fumadores, con lo que el RR es de 1,18. Lo siento por los que fumáis, pero El Dormilón no tenía razón: el tabaco es malo.

Con este ejemplo nos damos cuenta de lo importante que es lo que dijimos antes de que los resultados contrafactuales sean intercambiables. Si la distribución de edad es diferente entre expuestos y no expuestos y tenemos la desgracia de que la edad es una variable confusora, el resultado observado en los fumadores ya no será intercambiable con el resultado contrafactual de los no fumadores, y viceversa.

Control de variable de confusión

¿Podemos evitar este efecto?. Sí, lo que no podemos es evitar el efecto de la variable confusora, y esto supone un problema todavía mayor cuando desconocemos que nos puede jugar esta mala pasada. Por esto es esencial tomar una serie de medidas al diseñar el estudio que minimicen el riesgo de que ocurra y de que tengamos puertas traseras por donde se cuelen los datos.

Una de ellas es la aleatorización, con la que trataremos que ambos grupos sean similares en cuanto a la distribución de variables confusoras, conocidas y no conocidas. Otra sería restringir la inclusión en el estudio a un grupo determinado como, en este ejemplo, los menores de 50 años. El problema es que esto no podemos hacerlo para variables confusoras desconocidas. Otra tercera posibilidad es utilizar datos pareados, de tal forma que por cada fumador joven incluyamos un no fumador joven, y lo mismo para los mayores. Para aplicar este emparejamiento también hace falta conocer previamente el papel de la variable confusora.

Nos vamos…

¿Y qué hacemos una vez que ya hemos terminado el estudio y comprobamos con horror que hay una puerta trasera?. Lo primero, no desesperar. Siempre podemos utilizar los múltiples recursos de la epidemiología para calcular una medida de asociación ajustada que nos estime la relación entre exposición y efecto sin tener en cuenta el efecto de confusión. Además, hay varios métodos para hacer este análisis, unos más sencillos y otros más complejos, aunque todos ellos muy elegantes. Pero esa es otra historia…