Importancia clínica.

La importancia clínica debe dirigirnos a la hora de valorar los resultados de un estudio. Para ello, utilizaremos los intervalos de confianza.
Los llamados seres humanos tenemos la tendencia a ser demasiado categóricos. Nos gusta mucho ver las cosas blancas o negras, cuando la realidad es que la vida no es ni blanca ni negra, sino que se manifiesta en una amplia gama de grises. Hay quien piensa que la vida es de color de rosa o que el color depende del cristal con el que se mire, pero no lo creáis: la vida es de colores grises.
Y esa tendencia a ser demasiado categóricos nos lleva, en ocasiones, a sacar conclusiones muy diferentes sobre un tema en concreto según el color, blanco o negro, del cristal con el que lo miremos. No es raro que, sobre determinados temas, podamos observar opiniones opuestas.
Y lo mismo puede ocurrir en medicina. Cuando surge un nuevo tratamiento y empiezan a publicarse trabajos sobre su eficacia o su toxicidad, no es raro encontrar estudios muy similares en los que los autores llegan a conclusiones muy diferentes. Muchas veces esto se debe al empeño en ver las cosas blancas o negras, sacando conclusiones categóricas de parámetros como el valor de la significación estadística, el valor de la p. En realidad, en muchos de estos casos los datos no dicen cosas tan diferentes, pero tenemos que mirar la gama de grises que nos brindan los intervalos de confianza.
Como me imagino que no entendéis bien de qué leches estoy hablando, voy a tratar de explicarme mejor y de poner algún ejemplo.
No todo es blanco o negro
Ya sabéis que nunca nunca nunca podemos probar la hipótesis nula. Solo podemos rechazarla o ser incapaces de rechazarla (en este caso asumimos que es cierta, pero con una probabilidad de error). Por eso cuando queremos estudiar el efecto de una intervención planteamos la hipótesis nula de que el efecto no existe y diseñamos el estudio para que nos dé información sobre si podemos o no rechazarla. En el caso de rechazarla asumimos la hipótesis alternativa de que el efecto de la intervención existe. Una vez más, siempre con una probabilidad de error, que es el valor de la p o la significación estadística.
En resumen, si la rechazamos asumimos que la intervención tiene un efecto y si no podemos rechazarla asumimos que no la tiene. ¿Os dais cuenta?: blanco o negro. Esta interpretación tan simplista no tiene en cuenta la gama de grises que tienen que ver con factores relevantes como la importancia clínica, la precisión de la estimación o la potencia del estudio.
Importancia clínica: usa intervalos de confianza
En un ensayo clínico es habitual proporcionar la diferencia encontrada entre el grupo de intervención y el de control. Esta estimación es puntual pero, como el ensayo lo hemos hecho con una muestra de una población, lo correcto es acompañar la estimación puntual de un intervalo de confianza que nos proporcione el rango en el que se incluye el valor real de la población inaccesible con una probabilidad o confianza determinada. Por convenio, la mayor parte de las veces está confianza se establece en el 95%.
Este 95% se elige habitualmente porque suelen usarse también niveles de significación estadística del 5%, pero no debemos olvidar que es un valor arbitrario. La gran cualidad que tiene el intervalo de confianza frente a la p es que no permite establecer conclusiones dicotómicas, del tipo de blanco o negro.
El intervalo de confianza no es significativo cuando cruza la línea de efecto nulo, que es el 1 para riesgos relativos y odds ratios y el 0 para riesgos absolutos y diferencias de medias. Si solo miramos el valor de p solo podemos concluir si se alcanza o no significación estadística, llegando a veces a conclusiones diferentes con intervalos muy parecidos.
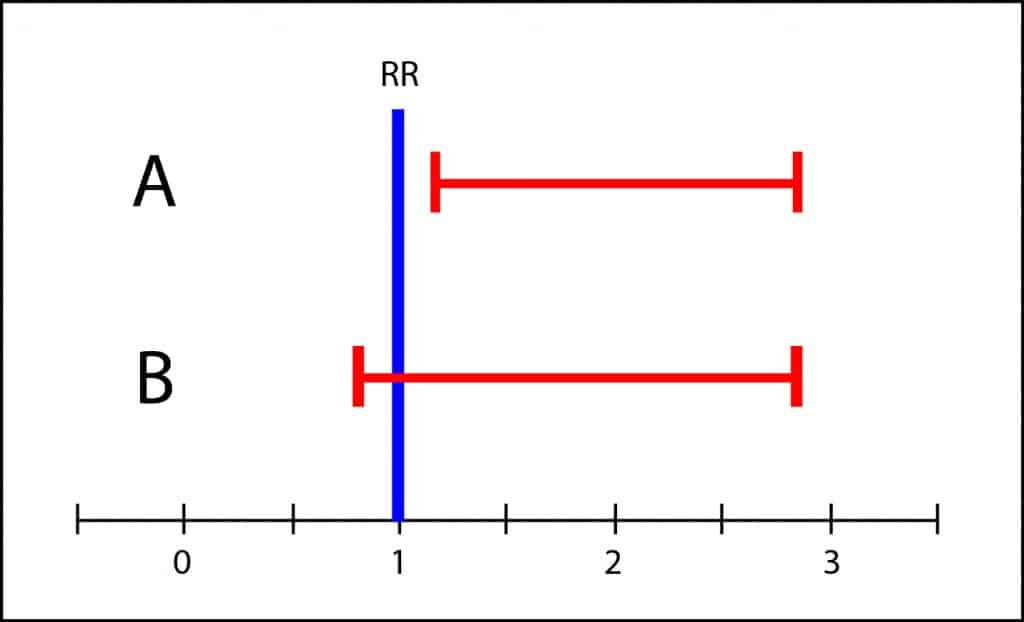
Sin embargo, el intervalo de B abarca desde algo menos de 1 hasta casi 3. Esto quiere decir que el valor de la población puede estar en cualquier valor del intervalo. Igual es 1, pero igual es 3, con lo que no es imposible que la toxicidad sea tres veces mayor que en el grupo de tratamiento. Si los efectos adversos son graves, no sería adecuado recomendar el tratamiento hasta disponer de estudios más concluyentes, con intervalos más precisos. Esto es a lo que me refiero con la gama de grises y la importancia clínica de los resultados. No es prudente sacar conclusiones en blanco y negro cuando hay solapamiento de los intervalos de confianza.
Así que seguid mi consejo. Haced menos caso a la p y buscad siempre la información sobre el rango posible de efecto que proporcionan los intervalos de confianza. No os quedéis con la significación estadística y valorad la importancia clínica de los resultados.
Nos vamos…
Y aquí lo dejamos por hoy. Podríamos hablar más acerca de situaciones similares pero cuando tratamos con estudios de eficacia, de superioridad o de no-inferioridad. Pero esa es otra historia…
