Ji-cuadrado para homogeneidad.

La prueba de la ji-cuadrado para homogeneidad compara proporciones de varias muestras para ver si proceden de la misma población

.

No hay ser más incomprendido que una oveja negra. Ya sabemos que habitualmente se usa el término para referirse a alguien que destaca dentro de un grupo o de una familia, generalmente por algún aspecto negativo. Pero las ovejas negras, en el sentido literal de la palabra, existen en el mundo real. Y como su lana es menos cotizada que la de las ovejas blancas, es fácil comprender el disgusto del pastor cuando ve una oveja negra en su rebaño.

Así que, nosotros, para compensar un poco la discriminación que sufren las ovejas negras vamos a contar ovejas, pero solo negras. Supongamos que durante un ataque alucinatorio decidimos que queremos convertirnos en pastores de ovejas. Nos vamos a una feria de ganado y buscamos un rebaño para comprarlo.

Contando ovejas

Pero claro, como somos nuevos en el negocio, nos tratarán de vender los rebaños con más ovejas negras que tengan en la feria. Así que tomamos tres muestras de 100 ovejas al azar de tres rebaños A, B y C y contamos el número de ovejas negras: 15, 17 y 12. ¿Quiere esto decir que el rebaño C es el que menos ovejas negras tiene?. No podemos saberlo solo con estos datos.

Puede ser que, por azar, hayamos seleccionado una muestra con menos ovejas negras cuando en realidad este rebaño sea el que más tenga. Como las diferencias son pequeñas, podemos aventurarnos a pensar que no hay grandes diferencias entre los tres rebaños y que las que observamos son debidas simplemente a un error del muestreo aleatorio. Esta será nuestra hipótesis nula: los tres rebaños son similares en cuanto a proporción de ovejas negras. Solo nos queda hacer nuestro contraste de hipótesis.

Sabemos que para comparar medias de diferentes poblaciones podemos utilizar el análisis de la varianza, que se basa en ver si las diferencias entre los grupos son mayores que las diferencias aleatorias debidas al error de muestreo. Ahora bien, en nuestro ejemplo no tenemos medias, sino porcentajes. ¿Cómo hacemos entonces el contraste?. Cuando lo que queremos comparar son contajes o porcentajes tenemos que recurrir a la prueba de la ji-cuadrado, pero el razonamiento es similar: ver si las diferencias entre los valores esperados y los observados son lo suficientemente grandes.

Prueba de ji-cuadrado para homogeneidad

Construyamos primero nuestra tabla de contingencia con los valores observados y esperados. Para calcular los valores esperados de una celda solo tenemos que multiplicar el marginal de su fila por el marginal de la columna y dividir por el total de la tabla. El que quiera saber por qué se hace así, puede leerlo en la entrada en la que lo explicábamos.

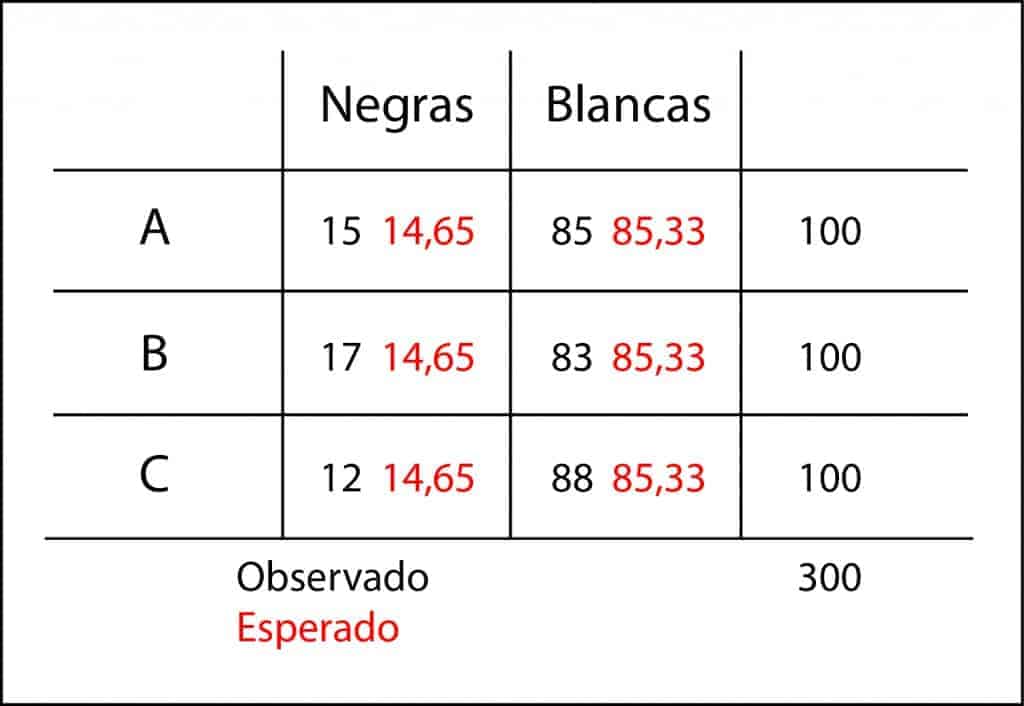
Una vez que tenemos los valores observado y esperado calculamos las diferencias entre ellos. Si ahora las sumáramos, las diferencias positivas se anularían con las negativas, así que previamente las elevamos al cuadrado, como hacíamos para calcular la desviación estándar de una distribución de datos.

Por último, hay que estandarizar estas diferencias dividiéndolas entre el valor esperado. No es lo mismo esperar uno y observar dos que esperar 10 y observar 11, aunque la diferencia en estos casos sea de uno. Y una vez que tenemos todos estos residuos estandarizados solo nos queda sumarlos para obtener un valor que alguien bautizó como estadístico de Pearson, más conocido como λ.

Si hacéis el cálculo veréis que λ = 1,01. ¿Y eso es mucho o poco?. Pues da la casualidad de que λ sigue, aproximadamente, una distribución de ji-cuadrado con, en nuestro caso, dos grados de libertad (filas-1 por columnas-1), así que podemos calcular la probabilidad de que valga 1,01. Este valor es el valor de la p, que es de 0,60. Al ser mayor que 0,05 no podemos rechazar nuestra hipótesis nula, así que concluiremos que no hay diferencias estadísticamente significativas entre los tres rebaños. Yo compraría el más barato de los tres.

Estos cálculos pueden hacerse con facilidad con una simple calculadora, pero suele ser más rápido utilizar cualquier programa de estadística, sobre todo si tenemos tablas de contingencia más grandes o con números más altos o con muchos decimales.

Nos vamos…

Y aquí dejamos de contar ovejas. Hemos visto la utilidad de la prueba de la j-cuadrado para el contraste de homogeneidad de poblaciones, pero la ji-cuadrado sirve para más cosas, como para contrastar la bondad del ajuste de dos poblaciones o la independencia de dos variables. Pero esa es otra historia…