Diagnóstico del modelo de regresión.

Vivimos en un mundo alocado, siempre corriendo de acá para allá y siempre con mil cosas en la cabeza. Así, no es raro que dejemos a medio terminar muchas de nuestras tareas.

Esto tendrá poca importancia en algunas ocasiones, pero habrá otras en las que dejar las cosas a medio terminar haga que la mitad que hayamos hecho no sirva para nada.

Y esto es precisamente lo que ocurre cuando aplicamos esta dejadez a nuestro tema de hoy: hacemos un experimento, calculamos una recta de regresión y nos ponemos a aplicarla sin más, olvidándonos de hacer un diagnóstico del modelo de regresión.

En estos casos, dejar las cosas a medias podrá tener como consecuencia que apliquemos a nuestra población un modelo predictivo que, en realidad, puede no ser válido.

El planteamiento del problema

Ya vimos en una entrada anterior cómo construir un modelo de regresión lineal simple. Como ya sabemos, la regresión lineal simple nos permite estimar cuál será el valor de una variable dependiente en función del valor que tome una segunda variable, que será la independiente, siempre que entre las dos variables exista una relación lineal.

Vimos también en un ejemplo cómo un modelo de regresión podía permitirnos estimar cuál sería la altura de un árbol si solo conocemos el volumen del tronco, aunque no tuviésemos disponible ningún árbol con ese volumen.

A nadie le extraña, pues, que las capacidades de predicción de los modelos de regresión se utilicen con profusión en la investigación biomédica. Y eso está bien, pero el problema es que, la inmensa mayoría de las veces, los autores que utilizan los modelos de regresión para comunicar los resultados de los estudios se olvidan de la validación y del diagnóstico del modelo de regresión.

Y llegados a este punto, alguno se preguntará: pero ¿es que los modelos de regresión hay que validarlos? Si ya tenemos los coeficientes del modelo, ¿hay que hacer algo más?

Pues sí, no basta con obtener los coeficientes de la recta y ponernos a hacer predicciones. Para estar seguros de que el modelo es válido hay que comprobar una serie de supuestos. Este proceso se conoce con el nombre de validación y diagnóstico del modelo de regresión.

Validación del modelo de regresión

Nunca debemos olvidar que nosotros solemos trabajar con muestras, pero lo que en realidad queremos es hacer inferencias sobre la población de la que procede la muestra, a la que no podemos acceder en su totalidad.

Una vez que calculamos los coeficientes de la recta de regresión utilizando, por ejemplo, el método de los mínimos cuadrados, y vemos que su valor es distinto de cero, debemos preguntarnos si es posible que en la población su valor sea cero y que los valores que hemos encontrado en nuestra muestra se deben a fluctuaciones aleatorias.

¿Y cómo podemos saber esto? Muy fácil, plantearemos un contraste de hipótesis para los dos coeficientes de la recta con la hipótesis nula de que el coeficiente vale, efectivamente, cero:

H₀ : β₀ = 0 y H₀ : β₁ = 0

Si podemos rechazar ambas hipótesis nulas, podremos aplicar la recta de regresión que hemos obtenido a nuestra población.

Si no podemos rechazar H₀ para β₀, la constante (interceptor) del modelo no será válida. Todavía podremos aplicar la recta, pero asumiendo que se origina en el eje de coordenadas. Pero si tenemos la desgracia de no poder rechazar la hipótesis nula para la pendiente (o para ninguno de los dos coeficientes), no podremos aplicar la recta a la población: la variable independiente no permitirá predecir el valor de la dependiente.

Este contraste de hipótesis puede hacerse de dos formas:

Si dividimos cada coeficiente por su error estándar, obtendremos un estadístico que sigue una distribución de la t de Student con n-2 grados de libertad. Podemos calcular el valor de p asociado a ese valor y resolver el contraste de hipótesis rechazando la hipótesis nula si el valor de p < 0,05.

1. Una forma un poco más compleja es fundamentar este contraste de hipótesis sobre un análisis de la varianza (ANOVA). Este método considera que la variabilidad de la variable dependiente se descompone en dos términos: uno explicado por la variable independiente y otro no asignado a ninguna fuente y que se considera no explicada (aleatoria).

Se puede obtener la estimación de la varianza del error de ambos componentes, explicado y no explicado. Si la variación debida a la variable independiente no supera a la del azar, el cociente de explicada/no explicada tendrá un valor próximo a uno. En caso contrario, se alejará de la unidad, tanto más cuanto mejores predicciones de la variable dependiente proporcione la variable independiente.

Cuando la pendiente (el coeficiente β₁) es igual a cero (bajo el supuesto de la hipótesis nula), este cociente sigue una distribución de la F de Snedecor con 1 y n-2 grados de libertad. Al igual que con el método anterior, podemos calcular el valor de p asociado al valor de F y rechazar la hipótesis nula si p < 0,05.

Veamos un ejemplo

Vamos a tratar de ver un poco más claro lo que acabamos de explicar recurriendo a un ejemplo práctico. Para ello, vamos a utilizar el programa estadístico R y uno de sus conjuntos de datos, trees, que recoge la circunferencia, volumen y altura de 31 observaciones sobre árboles.

Cargamos el conjunto de datos, ejecutamos la orden lm() para calcular el modelo de regresión y obtenemos su resumen con la función summary(), tal como podéis ver en la figura adjunta.

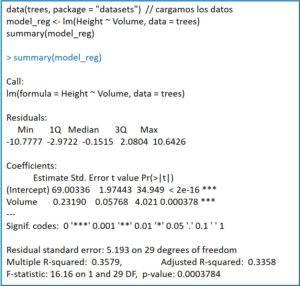
Si os fijáis, el programa muestra la estimación puntual de los coeficientes junto con su error estándar. Esto se acompaña de los valores del estadístico t con su significación estadística. En ambos casos, el valor de p < 0,05, por lo que rechazamos la hipótesis nula para los dos coeficientes de la recta. En otras palabras, ambos coeficientes son estadísticamente significativos.

A continuación, R nos proporciona una serie de datos (la desviación estándar de los residuos, el cuadrado del coeficiente de correlación múltiple o coeficiente de determinación y su valor ajustado) entre los que se encuentra el contraste F para validar el modelo. No hay sorpresas, p es menor de 0,05, por lo que podemos rechazar la hipótesis nula: el coeficiente β₁ es estadísticamente significativo y la variable independiente permite predecir los valores de la variable independiente.

Diagnóstico del modelo de regresión

Todo lo que hemos visto hasta ahora suelen proporcionarlo los programas estadísticos cuando pedimos el modelo de regresión. Pero no podemos dejar la tarea a medias. Una vez comprobado que los coeficientes son significativos, nos queda asegurar que se cumplen una serie de supuestos necesarios para que el modelo sea válido.

Estos supuestos son cuatro: linealidad, homocedasticidad, normalidad e independencia. Aquí, aunque utilicemos un programa de estadística, tendremos que trabajar un poco para comprobar estos supuestos y realizar un correcto diagnóstico del modelo regresión.

Supuesto de linealidad

Como ya hemos comentado, la relación entre la variable dependiente y la independiente debe ser lineal. Esto puede apreciarse con algo tan sencillo como un diagrama de puntos o de dispersión, que nos muestra el aspecto de la relación en el rango de valores observados de la variable independiente.

Si vemos que la relación no es lineal y tenemos un gran empeño en utilizar un modelo de regresión lineal, podemos intentar hacer una transformación de las variables y ver si así los puntos ya se distribuyen, más o menos, a lo largo de una recta.

Un método numérico que permite comprobar el supuesto de linealidad es la prueba RESET de Ramsey. Esta prueba contrasta si es necesario introducir términos cuadráticos o cúbicos para que desaparezcan los patrones sistemáticos en los residuos. Veamos qué significa esto.

Los residuos son la diferencia entre el valor real de la variable dependiente observado en el experimento y el valor estimado por el modelo de regresión. En la imagen anterior que muestra el resultado de la función summary() de R podemos ver la distribución de los residuos.

Para que el modelo sea correcto, la mediana debe estar próxima a cero y los valores absolutos de los residuos deben distribuirse de manera uniforme entre los cuartiles (similar entre máximo y mínimo y entre primer y tercer cuartil). En otras palabras, esto quiere decir que los residuos, si el modelo es correcto, siguen una distribución normal cuya media es cero.

Si vemos que esto no es así, los residuos estarán sesgados de forma sistemática y el modelo estará incorrectamente especificado. Lógicamente, si el modelo no es lineal, esta desviación de los residuos podría corregirse introduciendo en la ecuación de la recta un término cuadrático o cúbico. Claro que, entonces, ya no sería una regresión lineal ni la ecuación de una recta.

La hipótesis nula de la prueba de Ramsey dice que los términos cuadrático, cúbico, o ambos son iguales a cero (pueden contrastarse de forma conjunta o separada). Si no podemos rechazar la hipótesis nula, se asume que el modelo está correctamente especificado. En caso contrario, si rechazamos la hipótesis nula, el modelo tendrá errores de especificación y habrá que revisarlo.

Supuesto de homocedasticidad

Ya lo hemos comentado: los residuos deben distribuirse de forma homogénea para todos los valores de la variable de predicción.

Esto puede comprobarse de forma sencilla con un diagrama de dispersión que represente, en el eje de abscisas, las estimaciones de la variable dependiente para los distintos valores de la variable independiente y, en el eje de coordenadas, los residuos correspondientes. Se aceptará el supuesto de homocedasticidad si los residuos se distribuyen de forma aleatoria, en cuyo caso veremos una nube de puntos de forma similar en todo el rango de las observaciones de la variable independiente.

También disponemos de métodos numéricos para comprobar el supuesto de homocedasticidad, como la prueba de Breusch-Pagan-Godfrey, cuya hipótesis nula supone que se cumple este supuesto.

Supuesto de normalidad

También lo hemos dicho ya: los residuos deben distribuirse de forma normal.

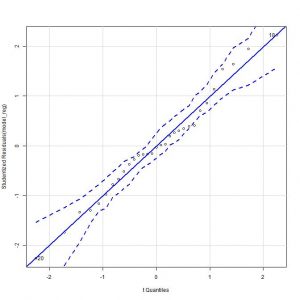
Una forma sencilla sería representar el gráfico de cuantiles teóricos de los residuos, en el que deberíamos ver su distribución a lo largo de la diagonal del gráfico.

También podremos aplicar un método numérico, como la prueba de Kolmogorov-Smirnov o la de Shapiro-Wilk.

Supuesto de independencia

Por último, los residuos deben ser independientes entre sí y no debe haber ningún tipo de correlación entre ellos.

Esto puede contrastarse realizando la prueba de Durbin-Watson, cuya hipótesis nula supone, precisamente, que los residuos son independientes.

Volvamos a nuestro ejemplo

Para ir terminando esta entrada, vamos a hacer el diagnóstico del modelo de regresión que hemos utilizado más arriba con nuestros árboles. Para hacerlo apto para todos los públicos, nos ayudaremos esta vez de la interfaz R-Commander, con lo que nos evitaremos escribir en línea de comandos, que siempre es más antipático.

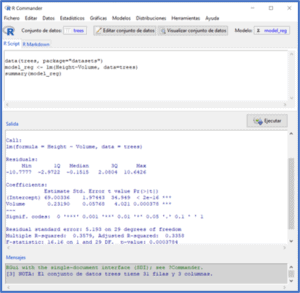
Para aquellos que no conozcáis muy bien R, os dejo en la primera pantalla los pasos previos para cargar los datos y calcular el modelo de regresión.

Empecemos con el diagnóstico del modelo.

Para comprobar si se cumple el supuesto de linealidad, comenzamos dibujando el gráfico de puntos entre las dos variables (opciones de menú Gráficas->Diagrama de dispersión). Si observamos el gráfico, vemos que los puntos se distribuyen, más o menos, a lo largo de una recta en sentido ascendente hacia la derecha.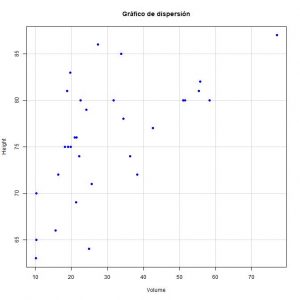

Si queremos hacer el método numérico, seleccionamos la opción del menú Modelos->Diagnósticos numéricos->Test RESET de no linealidad. R nos da un valor RESET = 2,52, con una p = 0,09. Como p > 0,05, no podemos rechazar la hipótesis nula de que el modelo es lineal, con lo que corroboramos la impresión que obtuvimos con el método gráfico.

Vamos con la homocedasticidad. Para el método gráfico recurrimos a la opción del menú Modelos->Gráficas->Gráficas básicas de diagnóstico. El programa nos proporciona 4 gráficas, pero ahora solo nos fijaremos en el primero de ellos, que representa los valores predichos por el modelo de la variable dependiente frente a los residuos.

Como puede verse, la dispersión de los puntos es mucho mayor para los valores más bajos de la variable dependiente, así que yo no me quedaría muy tranquilo respecto a si se cumple el supuesto de homocedasticidad. Los puntos deberían distribuirse de forma homogénea para todo el rango de valores de la variable dependiente.

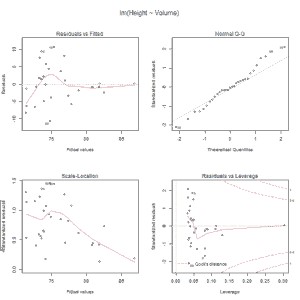
Vamos a ver qué dice el método numérico. Seleccionamos la opción del menú Modelos->Diagnósticos numéricos->Test de Breusch-Pagan para heterocedasticidad. El valor del estadístico BP que nos proporciona R es de 2,76, con un valor de p = 0,09. Como p > 0,05, no podemos rechazar la hipótesis nula, así que asumimos que se cumple el supuesto de homocedasticidad.

Pasamos a comprobar la normalidad de los residuos. Para el método gráfico de diagnóstico, seleccionamos la opción del menú Gráficas->Gráfica de comparación de cuantiles. Esta vez no hay duda, parece que los puntos se distribuyen a lo largo de la diagonal.

Para terminar, comprobemos el supuesto de independencia.

Seleccionamos la opción Modelos->Diagnósticos numéricos->Test de Durbin-Watson para autocorrelación. Se suele seleccionar un valor de rho distinto de cero, ya que es infrecuente conocer el sentido de la autocorrelación de los residuos, si esta existe. Lo hacemos así y R nos da un valor del estadístico DW = 1,53, con valor de p = 0,12.

En consecuencia, no podemos rechazar la hipótesis nula de que los residuos son independientes, cumpliéndose así la última condición para considerar el modelo como válido.

Nos vamos…

Y aquí lo vamos a dejar por hoy. Viendo lo laborioso de todo este procedimiento, uno puede caer en la tentación de perdonar e, incluso, comprender, a los autores que nos ocultan el diagnóstico de sus modelos de regresión. Pero esta excusa no es válida: los programas estadísticos lo hacen sin el mayor esfuerzo.

No penséis que con todo lo que hemos explicado hemos hecho todo lo que deberíamos antes de aplicar un modelo de regresión lineal simple con confianza.

Por ejemplo, no estaría de más valorar si hay observaciones influyentes que puedan tener un mayor peso en la formulación del modelo. O si hay valores extremos (outliers) que puedan distorsionar la estimación de la pendiente de la recta de regresión. Pero esa es otra historia…